
|
|
Выбор оптимальных режимов сварки внутренних микросоединений датчиков газовГазочувствительные датчики (химические сенсоры) находят широкое применение для контроля газовых технологических сред в микроэлектронике. Химические сенсоры основаны на изменении примесной проводимости в результате взаимодействия полупроводникового материала с активными газами. Концентрация газа при этом преобразуется непосредственно в электрический сигнал, для регистрации которого требуются относительно простые электрические схемы. Широкое распространение для газочувствительных датчиков получили полупроводниковые оксиды металлов, в частности, диоксид олова SnO2. Так как каждый газ характеризуется определенной энергией связи с поверхностью SnO2, то различные газы обладают индивидуальными значениями температур максимальной адсорбции. Для SnO2 большинство газов имеют температуры максимальной чувствительности в интервале 200-400 °С. Высокая чувствительность химических сенсоров к активным окисляющим (кислород, фтор) и восстанавливающим (водород, пары ацетона) газам, а также малая потребляемая мощность позволили изготавливать на их основе переносные и автономные портативные автоматические газоанализаторы. Для повышения чувствительности измерения контролируемых газов микросоединения проволока – пленка на контактных площадках должны иметь стабильные омические сопротивления. Качество соединений определяется множеством факторов: физико-механическими свойствами проволоки и пленочной металлизации; режимами микросварки; типом инструмента, формой и геометрическими размерами его рабочей площадки; наличием или отсутствием загрязнений на соединяемых поверхностях и т. д. В качестве металлизации контактных площадок кристаллов датчиков газов широко используется пленка платины, а формирование электрического контакта осуществляется проволокой микронных размеров из алюминия, золота или платины. Наибольшее распространение при монтаже внутренних микросоединений высокой надежности в датчиках газов получила проволока диаметром 0,03-0,05 мм из платины. Наиболее важными механическими свойствами привариваемой проволоки являются прочность и относительное удлинение. Для стабилизации свойств проволоки ее подвергают отжигу перед монтажом. Целью отжига является снижение механической прочности и повышение пластичности проволоки. Вопросам выбора оптимальных режимов сварки «расщепленным» электродом платиновой проволоки к платиновой металлизации контактных площадок датчиков газов посвящен данный раздел. Основной целью современного эксперимента с позиции производителя продукции является разработка математической модели, адекватно описывающей процесс и позволяющий, в конечном результате, осуществлять его управление. Статистические методы планирования эксперимента, являются одним из эмпирических способов получения математического описания сложных процессов. Представим процесс микросварки в виде «черного ящика» (рис. 6.32). Х1, Х2, …, Хn – входные параметры, действующие в исследуемом процессе. Y – выход системы, называемой функцией отклика, является функцией входных параметров. В этом случае задача выбора оптимальных режимов микросварки заключается в следующем: найти математическую модель процесса в виде некоторой функции: Y = f (Х1, Х2, …, Хn) и значения Хi, обеспечивающие экстремум (максимум) функции. Необходимо получить математическую модель процесса сварки платиновых выводов с платиновой металлизацией датчиков газов с целью определения оптимальных режимов сварки. В процессе проведения эксперимента варьировались три фактора: температура отжига проволоки T ºC (Х1), давление на сварочный электрод PЭ (Х2) и напряжение, подаваемое на сварочный электрод, U (Х3) (табл. 6.13). Время сварки во всех случаях составляла 0,1 с.
Рис. 6.32. Схема процесса сварки «расщепленным» электродом
В качестве критерия качества, а следовательно, функции отклика исследуемого процесса принята прочность микросоединений.
Табл. 6.13. Значение уровней варьирования
Для выбора оптимальных режимов монтажа микросоединений платиновой проволоки диаметров 0,05 мм к платиновой металлизации толщиной 0,003 мм датчиков газов использовалась импульсная сварка «расщепленным» электродом на установке УСМ-1С с использованием сварочного электрода с рабочей частью из вольфрама (рис. 6.33).
При сварке сдвоенным «расщепленным» электродом учитывается особенность выполнения соединений в изделиях, которая заключается в одностороннем расположении электродов, объединенных в жесткую конструкцию. Между электродами размещается электроизоляционная (слюда или синтетический корунд) прокладка толщиной 0,03-0,22 мм. Если диаметр проволочного вывода составляет 0,03-0,15 мм, то длинна и ширина торца каждого электрода соответственно составляют 0,02-0,1 мм и 0,08-0,6 мм. Материалом электродов кроме вольфрама может быть молибден или металлокерамический твердый сплав типа ВК8. Такие электроды выдерживают до 30-40 тыс. сварок. Платиновая пленка напылялась на подложку из кварца на установке с электроннолучевым испарителем. Давление остаточной атмосферы в камере вакуумной установки при напылении пленок составляло 1,33·10–2 Па. Кварцевые подложки при напылении подогревались до температуры 800 ºС. После напыления пленок в течение 30 мин приводился отжиг образцов при той же температуре. В процессе формирования сварного соединения участок проволока – контактная площадка при прохождении через него электрического тока вследствие выделения теплоты разогревается. Усилие прижатия электрода и время сварки зависит от материала и диаметра проволоки. Внешний вид микросоединений платиновой проволоки к пленке из платины представлен на рис. 6.34.
Рис. 6.34. Соединение платиновой проволоки с платиновой металлизацией, выполненное «расщепленным» электродом. Увеличение 350×
Механическая прочность оценивалась на отрыв проволоки под углом 90º к плоскости образца на установке УКПМ-1 с одновременным контролем характера разрушения. Для удобства обработки результатов опытов проводилось преобразование значений управляемых переменных (учитываемых в эксперименте факторов Хi) к безразмерным величинам: Хiб = (Хi – Хоi) / ∆Хi, где Хi – текущее значение i-го фактора; Хоi – базовое или начальное значение i-го фактора в центре плана; ∆Хi – значение интервала варьирования по i-му фактору. Таким образом, в безразмерной системе координат верхний уровень фактора при проведении эксперимента равен + 1, а нижний – 1 (при составлении матрицы планирования для упрощения заменяем на символы ‘+’ и ‘–‘). Поскольку в эксперименте используется 3 фактора, а предполагаемая математическая модель исследуемого процесса линейна, то она соответствует полиному вида: Y=b0+b1x1+b2x2+b3x3+b12x1x2+b13x1x3+b23x2x3+b123x1x2x3, где Y – значение функции отклика; x1, x2, x3 – значения исследуемых факторов; b0 – значение функции отклика в центре плана; b1, b2, b3 – коэффициенты, характеризующие степень влияния факторов на функцию отклика; b12, b13, b23, b12.3 – коэффициенты, характеризующие взаимовлияние факторов. При варьировании каждым из трех факторов (к = 3) на двух уровнях число опытов N будет составлять N = 2к = 23 = 8. Для каждой комбинации факторов было проведено 15 параллельных опытов (n = 15). Для проведения эксперимента по известной методике составлена матрица планирования полного факторного эксперимента (ПФЭ) типа 23, представленная в безразмерной форме в табл. 6.14 и в числовом выражении в табл. 6.15. Проведена оценка однородности дисперсий функции отклика в соответствии с критерием Кохрена, ее результаты (для N = 8 и n = 15: G = 0,157 ≤ Gкр = 0,29) позволяют сделать вывод о воспроизводимости эксперимента, а отклонения значений функции отклика носят случайный характер и вызваны влиянием неконтролируемых и неуправляемых факторов.
Табл. 6.14. Матрица планирования ПФЭ типа 23
Табл. 6.15. Зависимость прочности соединения от исследуемых факторов
Коэффициенты полинома вычислены по формуле
где bi – коэффициент полинома, соответствующий i-фактору; ξ – номера опытов; хξi – значение безразмерного фактора а матрице планирования, соответствующего ξ-строке и i-столбцу; yξ – значение отклика в ξ-опыте. Проверка значимости коэффициентов с помощью t-критерия Стьюдента показала, что коэффициенты b12, b13, b123 признаны статистически незначимыми, поэтому соответствующие им члены полинома исключаются из уравнения математической модели процесса. Остальные коэффициенты имеют следующие значения: b0 = 29,6; b1 = – 2,5; b2 = 3; b3 = 4, b23 = 0,6. Исключение членов полинома, включающих коэффициенты b12, b13, b123, означает, видимо, что взаимодействие соответствующих им факторов не оказывает влияния на функцию отклика (прочность соединений). Наименьшее влияние оказывает первый фактор (температура отжига проволоки). Влияние двух других факторов примерно равнозначно. Таким образом, математическая модель с учетом значимости коэффициентов полинома имеет вид: Y = b0 + b1x1+ b2x2 + b3x3+ b23x2x3; Y = 29,6 – 2,5·x1+ 3·x2 + 4·x3 + 0,6·x2x3. Теоретические значения прочности соединений для каждого опыта yςt, предсказываемые математической моделью, вычислены и представлены в табл. 6.15. Проведена проверка адекватности математической модели результатам эксперимента по известным формулам. Вычисленная дисперсия адекватности S2ад = 0,6 не превышает дисперсию опыта S2{y} = 13,3. Следовательно, можно сделать вывод о том, что полученная математическая модель адекватно представляет результаты эксперимента. Исследование функции на экстремум показало, что максимальное значение прочности соединений достигается при следующих значениях безразмерных факторов Х1 = – 1; Х2 = + 1; Х3 = + 1. Следовательно, оптимальными параметрами процесса исследуемого процесса будут следующие значения: Т = 400 ºС, РЭ = 16 МПа, U = 500 мВ. Максимальная теоретическая прочность соединений, предсказываемая математической моделью при этих значениях параметров, составляет 39,6 сН. Экспериментальные значения прочности микросоединений платина – платина, полученные на оптимальных режимах сварки, показали хорошее совпадение с теоретическими расчетами. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

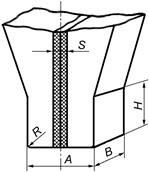 Рис. 6.33. Геометрия рабочей части «расщепленного» электрода: A и В – ширина и длина рабочей части; Н – высота прямоугольной части электрода; R – радиус электрода; S – межэлектродный зазор
Рис. 6.33. Геометрия рабочей части «расщепленного» электрода: A и В – ширина и длина рабочей части; Н – высота прямоугольной части электрода; R – радиус электрода; S – межэлектродный зазор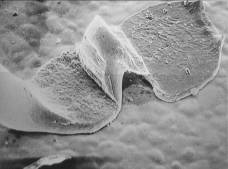
 ,
,