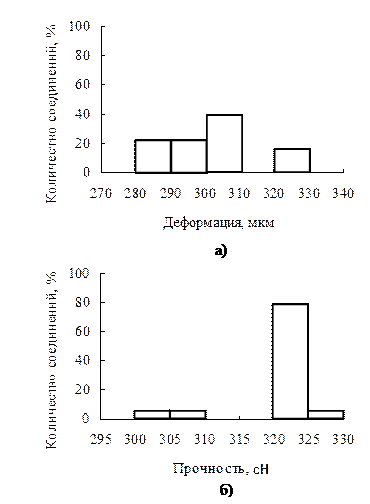Выбор оптимального режима УЗС соединения Al-Ag

После пайки кристаллов присоединение алюминиевых выводов к контактным площадкам кристалла и траверсам корпуса проводят ультразвуковой сваркой.

Качество соединений определяется множеством факторов: физико-механическими свойствами проволоки и металлизации; режимами УЗС; материалом инструмента, геометрическими формой и размерами его рабочей площадки; наличием или отсутствием загрязнений на соединяемых поверхностях и т. д.

Вопросу оптимизации режимов УЗС алюминиевой проволоки с серебряной металлизацией корпусов ППИ посвящен данный раздел. Представим процесс УЗС в виде «черного ящика» (рис. 6.30). Х₁, Х₂, …, Х_n – входные параметры, действующие в исследуемом процессе. Y – выход системы, называемый функцией отклика, является функцией входных параметров. В этом случае задача выбора оптимальных режимов УЗС заключается в следующем: найти математическую модель процесса в виде некоторой функции Y=f(Х₁, Х₂,…, Х_n) и значения Х_i, обеспечивающие экстремум (максимум) функции.

Рис. 6.30. Условное представление процесса УЗС

Необходимо получить математическую модель процесса УЗС алюминиевых проволочных выводов с серебряным гальваническим покрытием корпусных деталей СПП, с целью определения оптимальных режимов сварки.

В процессе проведения эксперимента варьировались три фактора: усилие нагружения на микросварочный инструмент (Х₁), мощность УЗ генератора (Х₂) и время сварки (Х₃) (табл. 6.11). В качестве критерия качества, а, следовательно, функции отклика исследуемого процесса принята прочность соединений. Прочность соединений определялась натяжением вывода под углом 90º к плоскости образца до разрушения соединений с одновременным контролем характера разрушения.

Табл. 6.11. Значения уровней варьирования

Примечание: мощность генератора УЗ колебаний (Х₂, дел.) устанавливается по числу делений регулятора мощности в установке УЗ-сварки.

Для проведения экспериментальных исследований осаждение серебра на медные пластины проводили в электролите следующего состава (г/л): AgCl – 40; K₄[Fe(CN₆)]3H₂O – 200; K₂CO₃ – 20. В качестве анодов использовались пластины из чистого серебра. Режимы осаждения: I_к = 1-1,5 А/дм², температура электролита 50 ºC, время 10 мин для толщины покрытия 6 мкм. После осаждения покрытий образцы отмывались в дистиллированной воде. Перед сваркой медные пластины с серебряным покрытием отжигались в водороде при температуре 390 ± 20 ºC с целью имитации процесса напайки кристаллов на основания корпусов. Предварительный отжиг образцов в кислороде не проводился из-за образования на поверхности серебряного покрытия оксидной пленки Ag₂O толщиной 500-600 Å. Оксидная пленка Ag₂O обеспечивает необходимое растекание припоя при пайке, но при сварке не способствует заданному качеству сварных соединений.

Для оценки влияния параметров УЗС на качество микросоединений алюминиевой проволоки с серебряной металлизацией использовали проволоку марки АОЦПоМ (ТУ 6365‑051‑46594157‑2004) диаметром 250 мкм. Химический состав проволоки, %: Si – 0,01; Cu – 0,01; Mg – 0,01; Mn – 0,01; Fe – 0,01; Sb ≤ 0,02; Ti – (0,003-0,08); Zn – (0,03-0,28); Al – остальное. Разварку выводов производили на установке для ультразвуковой сварки типа У-153 инструментом с треугольной канавкой на рабочем торце марки КУТ-41-250-600 (ОСТ 11 31 5001.8-92).

Для удобства обработки результатов проводится преобразование значений управляемых переменных (учитываемых в эксперименте факторов Х_i) к безразмерным величинам

Х_iб=(Х_i-X_oi)/ΔХ_i,

где Х_i – текущее значение i-го фактора; X_oi – базовое или начальное значение i-го фактора в центре плана; ΔХ_i – значение интервала варьирования по i-му фактору.

Поскольку в эксперименте используются 3 фактора, а предполагаемая математическая модель исследуемого процесса линейна, то она соответствует полиному вида

Y=b₀+b₁x₁+b₂x₂+b₃x₃+b₁₂x₁x₂+b₁₃x₁x₃+b₂₃x₂x₃+b₁₂₃x₁x₂x₃,

где Y – значение функции отклика; x₁x₂x₃ – значения исследуемых факторов; b₀ – значение функции отклика в центре плана; b₁, b₂, b₃ – коэффициенты, характеризующие степень влияния факторов на функцию отклика; b₁₂, b₁₃, b₂₃, b₁₂₃ – коэффициенты, характеризующие взаимовлияние факторов.

При варьировании каждым из трех факторов (к = 3) на двух уровнях число опытов N будет составлять N = 2^к = 2³ = 8. Для каждой комбинации факторов было проведено 15 параллельных опытов (n = 15).

По известной методике составлена матрица планирования полного факторного эксперимента типа 2³, представленная в табл. 6.12.

Табл. 6.12. Матрица планирования и результаты полного факторного эксперимента

Проведена оценка однородности дисперсий функции отклика в соответствии с критерием Кохрена, ее результаты (для N = 8 и n = 15: σ_max = 0,2787 ≤ 0,29 = σ_кр) позволяют сделать вывод о воспроизводимости эксперимента, а отклонения значений функции отклика носят случайный характер и вызваны влиянием неконтролируемых и неуправляемых факторов.

Вычислены коэффициенты полинома по формуле

,

где b_i – коэффициент полинома, соответствующий i-фактору; ξ = 1, …, N – номера опытов; x_ξi – значение безразмерного фактора в матрице планирования, соответствующего ξ-строке и i-столбцу; y_ξ – значение функции отклика в ξ-опыте.

Проверка значимости коэффициентов с помощью t-критерия Стьюдента показала, что коэффициенты b₁, b₁₂, b₁₃, b₂₃ признаны статистически незначимыми, поэтому соответствующие им члены полинома исключаются из уравнения математической модели процесса. Остальные коэффициенты имеют следующие значения: b₂ = – 13,59; b₃ = – 12,41; b₁₂₃ = – 3,31; b₀ = 288,4. Исключение члена полинома, соответствующего фактору х₁, означает, видимо, что этот фактор, а именно, усилие инструмента в выбранном интервале его значений не оказывает влияния на функцию отклика (прочность соединений). Влияние двух других факторов примерно равнозначно. Некоторое влияние оказывает взаимодействие трех факторов.

Таким образом, математическая модель с учетом значимости коэффициентов полинома имеет вид

Y = b₀+b₂x₂+b₃x₃+b₁₂₃x₁x₂x₃,

Y = 288,4 – 13,59x₂ – 12,41x₃ – 3,31x₁x₂x₃.

Теоретические значения прочности соединений для каждого опыта y_ςt, предсказываемые математической моделью, вычислены и представлены в табл. 6.12.

Проведена проверка адекватности математической модели результатам эксперимента. По известным формулам, вычислена дисперсия адекватности S²_ад = 21,45, которая не превышает дисперсию опыта S²{y} = 165, следовательно, можно сделать вывод о том, что полученная математическая модель адекватно представляет результаты эксперимента.

Полученная функция исследована на экстремум. Максимальное значение прочности соединений достигается при следующих значениях безразмерных факторов: х₁^опт = – 1; х₂^опт = – 1; х₃^опт = – 1. Следовательно, оптимальными параметрами процесса УЗС будут следующие значения: Q_опт = 250 сН; W_опт = 5,8 дел; τ_опт = 50 мс. Максимальная теоретическая прочность соединений при этих значениях параметров, предсказываемая математической моделью, составляет 317,71 сH.

Прочность соединений в значительной степени зависит от механических свойств проволоки в состоянии поставки. С целью стабилизации прочности и пластичности проволоки проводят ее отжиг перед сваркой. Перед проведением исследований проволоку отжигали в вакууме при Т=210±10 ºС в течение 7 мин. После отжига проволока имела следующие свойства: σ_т = 31-33 МПа, σ_в = 69-71 МПа и твердость в пределах 210-310 МПа.

Для экспериментальной оценки качества микросоединений Al-Ag на оптимальных режимах было разварено по 50 образцов. Деформация проволоки в зоне сварки определялась под микроскопом с точностью ±2 мкм. Анализ прочности соединений показал, что разрушение происходит, в основном, на участке перехода сварного соединения в проволоку.

На рис. 6.31 представлены гистограммы деформации алюминиевой проволоки и прочности соединений алюминиевой проволоки с серебряным покрытием, сформированных на оптимальных режимах УЗС. Из рис. 6.31 видно, что соединения Al-Ag имеют стабильную прочность в пределах 320-325 сН.

Для прогнозирования надежности СПП, имеющих соединение Al-Ag, необходим анализ данной контактной пары. Известно, что диаграмма состояния Al-Ag со стороны алюминия относится к эвтектическому типу. Растворимость серебра в твердом алюминии существенно зависит от температуры:

Увеличение содержания серебра приводит к повышению удельного электросопротивления сплава Al-Ag:

Рис. 6.31. Гистограммы распределения деформации алюминиевой проволоки (а) и прочности соединений алюминиевой проволоки с серебряным покрытием траверс корпусов (б)

Зависимость растворимости серебра в алюминии от температуры приводит к упрочнению сплавов Al-Ag при термической обработке (закалке и старении). В процессе закалки и старения твердость по Бринеллю у сплава с 8,7 % Ag увеличивается с 363 до 710 МПа и предел прочности со 120 до 210 МПа, а у сплава с 20 % Ag предел прочности повышается со 180 до 340 МПа. Повышение концентрации серебра в сплаве Al-Ag до 10 % повышает модуль упругости алюминия (каждый процент серебра на 527 МПа).

Не нашли, что искали? Воспользуйтесь поиском по сайту: