|
Лекция 41. Проективные преобразования плоскости. Группа аффинных преобразований плоскости как подгруппа группы проективных преобразований.
Проективным отображением проективной плоскости  на проективную плоскость на проективную плоскость  называется взаимно однозначное отображение плоскости называется взаимно однозначное отображение плоскости 
на плоскость  , при котором три любые точки плоскости , при котором три любые точки плоскости  , принадлежащие одной прямой, переходят в три точки плоскости , принадлежащие одной прямой, переходят в три точки плоскости  , также принадлежащие одной прямой. , также принадлежащие одной прямой.
Проективное отображение проективной плоскости  на себя называется проективным преобразованием проективной плоскости. на себя называется проективным преобразованием проективной плоскости.
Таким образом, определение проективного отображения плоскости  наплоскость наплоскость  и определение проективного преобразования плоскости и определение проективного преобразования плоскости  точно такие же, как и определения аффинного отображения и аффинного преобразования. Следует, однако, иметь в виду, что эти определения относятся к разным объектам: определение аффинного отображения и аффинного преобразования дается для евклидовой плоскости, а определение проективного отображения и проективного преобразования – для проективной плоскости. Этим и объясняется глубокое различие свойств аффинных и проективных отображений и преобразований. точно такие же, как и определения аффинного отображения и аффинного преобразования. Следует, однако, иметь в виду, что эти определения относятся к разным объектам: определение аффинного отображения и аффинного преобразования дается для евклидовой плоскости, а определение проективного отображения и проективного преобразования – для проективной плоскости. Этим и объясняется глубокое различие свойств аффинных и проективных отображений и преобразований.
Рассмотрим множество всех проективных преобразований проективной плоскости  . Пусть . Пусть  и и  – два любых проективных преобразования плоскости – два любых проективных преобразования плоскости  . Произведение . Произведение   является взаимно однозначным преобразованием и переводит три любые точки плоскости является взаимно однозначным преобразованием и переводит три любые точки плоскости  , принадлежащие одной прямой, в три точки плоскости , принадлежащие одной прямой, в три точки плоскости  , также принадлежащие одной прямой. , также принадлежащие одной прямой.
Следовательно,   – проективное преобразование. Преобразование – проективное преобразование. Преобразование  , обратное преобразованию , обратное преобразованию  , – взаимно однозначно. Преобразование , – взаимно однозначно. Преобразование  три любые точки три любые точки  плоскости плоскости  , принадлежащие одной прямой, переводит в точки , принадлежащие одной прямой, переводит в точки  также принадлежащие одной прямой. В самом деле, предполагая, что точки также принадлежащие одной прямой. В самом деле, предполагая, что точки  принадлежат одной прямой и допуская, что их прообразы принадлежат одной прямой и допуская, что их прообразы  при преобразовании при преобразовании  не лежат на одной прямой, не лежат на одной прямой,
докажем, что при преобразовании  все точки плоскости все точки плоскости  отображаются в точки прямой отображаются в точки прямой  , а значит, , а значит,  – невзаимно однозначное преобразование. – невзаимно однозначное преобразование.
Итак,  – проективное преобразование. Таким образом, множество всех проективных преобразований проективной плоскости образует группу, называемую группой проективных преобразований проективной плоскости. – проективное преобразование. Таким образом, множество всех проективных преобразований проективной плоскости образует группу, называемую группой проективных преобразований проективной плоскости.
При проективном отображении  проективной плоскости проективной плоскости  на проективную плоскость на проективную плоскость  ( и при проективном преобразовании плоскости ( и при проективном преобразовании плоскости  ) множество всех точек прямой ) множество всех точек прямой  отображается и притом взаимно однозначно на множество всех точек некоторой прямой отображается и притом взаимно однозначно на множество всех точек некоторой прямой  (это следует из того, что (это следует из того, что  – также проективное отображение плоскости – также проективное отображение плоскости  на плоскость на плоскость  ). ).
Прямая  называется образом прямой называется образом прямой  , а прямая , а прямая  прообразом прямой прообразом прямой  при преобразовании при преобразовании  . .
Множество всех проективных преобразований плоскости, каждое из которых отображает на себя какую-нибудь фиксированную прямую, образует подгруппу группы проективных преобразований. В самом деле, произведение 
проективных преобразований, каждое из которых отображает прямую  на себя, будет также отображать прямую на себя, будет также отображать прямую  на себя. Преобразование на себя. Преобразование  будет отображать прямую будет отображать прямую  на себя, если преобразование на себя, если преобразование  отображает отображает  на себя. на себя.
В частности, если проективная плоскость задана в виде первой модели, то множество 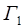 всех проективных преобразований плоскости, отображающих на себя несобственную прямую, будет подгруппой группы всех проективных преобразований плоскости, отображающих на себя несобственную прямую, будет подгруппой группы  проективных преобразований плоскости. проективных преобразований плоскости.
Каждое из проективных преобразований подгруппы 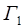 переводит собственные точки плоскости переводит собственные точки плоскости  в собственные точки плоскости в собственные точки плоскости  . В самом деле, если . В самом деле, если
бы какая-нибудь собственная точка плоскости  каким-нибудь проективным преобразованием из каким-нибудь проективным преобразованием из 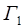 переводилась в несобственную, то три точки переводилась в несобственную, то три точки  и любые две несобственные точки переводились бы в три несобственные точки, а значит, при преобразовании, обратном рассматриваемому (также проективном), и любые две несобственные точки переводились бы в три несобственные точки, а значит, при преобразовании, обратном рассматриваемому (также проективном),
три несобственные точки переходили бы в две несобственные и в одну собственную. Это невозможно, ибо три несобственные точки принадлежат одной прямой, а две несобственные и одна собственная не принадлежат одной прямой.
Из сказанного следует, что любое преобразование из 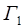 порождает в плоскости порождает в плоскости  , пополнением которой получается плоскость , пополнением которой получается плоскость  , аффинное преобразование. Группе , аффинное преобразование. Группе 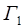 всех проективных преобразований плоскости всех проективных преобразований плоскости  соответствует в указанном смысле группа всех аффинных преобразований плоскости соответствует в указанном смысле группа всех аффинных преобразований плоскости  . .
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 на проективную плоскость
на проективную плоскость  называется взаимно однозначное отображение плоскости
называется взаимно однозначное отображение плоскости  и
и  – два любых проективных преобразования плоскости
– два любых проективных преобразования плоскости  , обратное преобразованию
, обратное преобразованию  плоскости
плоскости  также принадлежащие одной прямой. В самом деле, предполагая, что точки
также принадлежащие одной прямой. В самом деле, предполагая, что точки  при преобразовании
при преобразовании  , а значит,
, а значит,  отображается и притом взаимно однозначно на множество всех точек некоторой прямой
отображается и притом взаимно однозначно на множество всех точек некоторой прямой  (это следует из того, что
(это следует из того, что 
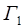 всех проективных преобразований плоскости, отображающих на себя несобственную прямую, будет подгруппой группы
всех проективных преобразований плоскости, отображающих на себя несобственную прямую, будет подгруппой группы  проективных преобразований плоскости.
проективных преобразований плоскости. и любые две несобственные точки переводились бы в три несобственные точки, а значит, при преобразовании, обратном рассматриваемому (также проективном),
и любые две несобственные точки переводились бы в три несобственные точки, а значит, при преобразовании, обратном рассматриваемому (также проективном), , пополнением которой получается плоскость
, пополнением которой получается плоскость