|
Лекция 32. Диаметральные плоскости поверхностей, сопряженные некоторому направлению.
Теорема 1. Геометрическим местом середин параллельных хорд поверхности второго порядка является плоскость. Эта плоскость называется диаметральной плоскостью данной поверхности, сопряженной хордам данного направления. Если поверхность второго порядка задана относительно общей
Декартовой системы координат общим уравнением

а ее хорды коллинеарны вектору  ( не имеющему асимптотического направления), то уравнение диаметральной плоскости, сопряженной этим хордам, имеет вид ( не имеющему асимптотического направления), то уравнение диаметральной плоскости, сопряженной этим хордам, имеет вид

 . (2) . (2)
Из уравнения (2) следует, что все диаметральные плоскости поверхностей второго порядка содержат геометрическое место ее центров, если оно не пусто,
так как уравнение (2) удовлетворяется, если

Вектор  некомпланарен диаметральной плоскости, сопряженной его направлению, так как главный вектор плоскости (2) имеет координаты некомпланарен диаметральной плоскости, сопряженной его направлению, так как главный вектор плоскости (2) имеет координаты
 , ,
откуда

 , ,
Теорема 2. Если существует вектор  неасимптотического направления, компланарный диаметральной плоскости, сопряженной хордам поверхности второго порядка, коллинеарных вектору неасимптотического направления, компланарный диаметральной плоскости, сопряженной хордам поверхности второго порядка, коллинеарных вектору  , то вектор , то вектор  будет компланарен диаметральной плоскости, сопряженной хордам этой поверхности, коллинеарным вектору будет компланарен диаметральной плоскости, сопряженной хордам этой поверхности, коллинеарным вектору  . .
Доказательство. Пусть вектор 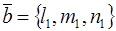 компланарен плоскости (2) и не имеет асимптотического направления поверхности (1). Тогда компланарен плоскости (2) и не имеет асимптотического направления поверхности (1). Тогда
 , ,
или
 , ,
а это и означает, что вектор  компланарен диаметральной плоскости, сопряженным хордам, коллинеарным вектору компланарен диаметральной плоскости, сопряженным хордам, коллинеарным вектору  . .
Из доказанной теоремы следует, что если диаметральные плоскости  и и  , сопряженные направлениям двух неколлинеарных векторов , сопряженные направлениям двух неколлинеарных векторов  и и  ( не имеющих асимптотического направления) пересекаются, и прямая их пересечения не имеет асимптотического направления относительно поверхности второго порядка, то диаметральная плоскость, сопряженная направлению хорд поверхности, параллельных этой прямой, компланарна векторам ( не имеющих асимптотического направления) пересекаются, и прямая их пересечения не имеет асимптотического направления относительно поверхности второго порядка, то диаметральная плоскость, сопряженная направлению хорд поверхности, параллельных этой прямой, компланарна векторам  и и  . Мы получаем в этом случае три диаметральные плоскости, обладающие тем свойством, что любая из них сопряжена с направлением прямой, по которой пересекаются две другие. . Мы получаем в этом случае три диаметральные плоскости, обладающие тем свойством, что любая из них сопряжена с направлением прямой, по которой пересекаются две другие.
Замечание. При определении центра поверхности второго порядка, асимптотических направлений, диаметральной плоскости и при доказательстве ряда теорем, связанных с этими определениями, предполагалось использование “мнимых “ точек.
Можно включить и рассматриваемую поверхность второго порядка, заданную общим уравнением  относительно общей декартовой системы координат, в семейство поверхностей относительно общей декартовой системы координат, в семейство поверхностей  . Для эллипсоида и мнимого конуса такое семейство будет включать в себя все эллипсоиды, гомотетичные друг другу, причем центром гомотетии будет их общий центр. Для гиперболоидов и конуса второго порядка семейство . Для эллипсоида и мнимого конуса такое семейство будет включать в себя все эллипсоиды, гомотетичные друг другу, причем центром гомотетии будет их общий центр. Для гиперболоидов и конуса второго порядка семейство  будет состоять из всех соасимптотических гиперболоидов, т.е. гомотетичных между собой однополостных и двуполостных гиперболоидов и их общего асимптотического конуса. Для параболоидов семейства будет состоять из всех соасимптотических гиперболоидов, т.е. гомотетичных между собой однополостных и двуполостных гиперболоидов и их общего асимптотического конуса. Для параболоидов семейства  будет состоять из поверхностей, полученных параллельным переносом данной поверхности вдоль ее оси симметрии. Для остальных поверхностей семейства будет состоять из поверхностей, полученных параллельным переносом данной поверхности вдоль ее оси симметрии. Для остальных поверхностей семейства  будут характеризоваться их сечениями плоскостью, не параллельной образующим. будут характеризоваться их сечениями плоскостью, не параллельной образующим.
Все определения и доказательства теорем для семейств  могут быть проведены с использованием только точек трехмерного евклидова пространства и потому все они инвариантны относительно преобразования системы координат, так как аналитические выводы, относящиеся к центру, асимптотическим направлениям, диаметральным плоскостям, не зависят от свободного члена общего уравнения поверхности. могут быть проведены с использованием только точек трехмерного евклидова пространства и потому все они инвариантны относительно преобразования системы координат, так как аналитические выводы, относящиеся к центру, асимптотическим направлениям, диаметральным плоскостям, не зависят от свободного члена общего уравнения поверхности.
Определение. Особым направлением относительно поверхности второго порядка называется направление прямой, параллельной всем диаметральным плоскостям этой поверхности.
Теорема 3. Пусть относительно общей декартовой системы координат задана поверхность второго порядка общим уравнением

Тогда если это уравнение является уравнением центральной поверхности (т.е. поверхности, имеющей единственный центр), то у нее нет особых направлений. Все остальные поверхности имеют особые направления. Для того чтобы ненулевой вектор  имел особое направление относительно поверхности (3), необходимо и достаточно, чтобы его координаты удовлетворяли соотношениям имел особое направление относительно поверхности (3), необходимо и достаточно, чтобы его координаты удовлетворяли соотношениям
 (4) (4)
Доказательство. Из уравнения (2) следует, что вектор  имеет особое направление тогда и только тогда, когда выполняется равенство имеет особое направление тогда и только тогда, когда выполняется равенство
 , ,
или

где  – любой вектор, не имеющий асимптотического направления. Так как всегда можно выбрать три неколлинеарных вектора – любой вектор, не имеющий асимптотического направления. Так как всегда можно выбрать три неколлинеарных вектора  , имеющих относительно поверхности (3) неасимптотическое направление, то однородное относительно , имеющих относительно поверхности (3) неасимптотическое направление, то однородное относительно  уравнение (5) имеет три линейно независимых решения уравнение (5) имеет три линейно независимых решения
 , а это возможно тогда и только тогда, когда все коэффициенты при , а это возможно тогда и только тогда, когда все коэффициенты при
 в уравнении (5) обращаются в нуль; таким образом, соотношения (4) выполняются. Если поверхность имеет единственный центр, то в уравнении (5) обращаются в нуль; таким образом, соотношения (4) выполняются. Если поверхность имеет единственный центр, то

и, значит, система (4) не имеет ненулевых решений  , особых направлений нет. , особых направлений нет.
Для всех остальных поверхностей  и система (4) имеет ненулевые решения. и система (4) имеет ненулевые решения.
Если ранг матрицы

равен 2 (поверхности II и III групп), то система (4) имеет ненулевые решения
 , но не имеет двух линейно независимых решений. Это значит, что поверхности II и III групп имеют лишь одно особое направление. Составляя систему (4) для простейших уравнений этих поверхностей, убедимся, что особое направление – это направление оси , но не имеет двух линейно независимых решений. Это значит, что поверхности II и III групп имеют лишь одно особое направление. Составляя систему (4) для простейших уравнений этих поверхностей, убедимся, что особое направление – это направление оси  в простейших уравнениях этих поверхностей. в простейших уравнениях этих поверхностей.
Если ранг матрицы  равен 1, то система (4) имеет два линейно независимых решения равен 1, то система (4) имеет два линейно независимых решения  и и 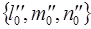 . Все решения системы (4) являются всеми линейными комбинациями этих двух. Это значит, что для поверхностей . Все решения системы (4) являются всеми линейными комбинациями этих двух. Это значит, что для поверхностей
IV и V групп существует плоскость, такая, что любая прямая, параллельная этой плоскости, имеет особое направление и этими направлениями исчерпываются все особые направления этих поверхностей (это плоскость  в простейших уравнениях (IV) и (V)). в простейших уравнениях (IV) и (V)).
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|



 ( не имеющему асимптотического направления), то уравнение диаметральной плоскости, сопряженной этим хордам, имеет вид
( не имеющему асимптотического направления), то уравнение диаметральной плоскости, сопряженной этим хордам, имеет вид
 . (2)
. (2)
 некомпланарен диаметральной плоскости, сопряженной его направлению, так как главный вектор плоскости (2) имеет координаты
некомпланарен диаметральной плоскости, сопряженной его направлению, так как главный вектор плоскости (2) имеет координаты ,
,
 ,
,  неасимптотического направления, компланарный диаметральной плоскости, сопряженной хордам поверхности второго порядка, коллинеарных вектору
неасимптотического направления, компланарный диаметральной плоскости, сопряженной хордам поверхности второго порядка, коллинеарных вектору  , то вектор
, то вектор 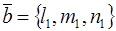 компланарен плоскости (2) и не имеет асимптотического направления поверхности (1). Тогда
компланарен плоскости (2) и не имеет асимптотического направления поверхности (1). Тогда ,
, ,
, .
. и
и  , сопряженные направлениям двух неколлинеарных векторов
, сопряженные направлениям двух неколлинеарных векторов  и
и  ( не имеющих асимптотического направления) пересекаются, и прямая их пересечения не имеет асимптотического направления относительно поверхности второго порядка, то диаметральная плоскость, сопряженная направлению хорд поверхности, параллельных этой прямой, компланарна векторам
( не имеющих асимптотического направления) пересекаются, и прямая их пересечения не имеет асимптотического направления относительно поверхности второго порядка, то диаметральная плоскость, сопряженная направлению хорд поверхности, параллельных этой прямой, компланарна векторам  относительно общей декартовой системы координат, в семейство поверхностей
относительно общей декартовой системы координат, в семейство поверхностей  . Для эллипсоида и мнимого конуса такое семейство будет включать в себя все эллипсоиды, гомотетичные друг другу, причем центром гомотетии будет их общий центр. Для гиперболоидов и конуса второго порядка семейство
. Для эллипсоида и мнимого конуса такое семейство будет включать в себя все эллипсоиды, гомотетичные друг другу, причем центром гомотетии будет их общий центр. Для гиперболоидов и конуса второго порядка семейство 
 имел особое направление относительно поверхности (3), необходимо и достаточно, чтобы его координаты удовлетворяли соотношениям
имел особое направление относительно поверхности (3), необходимо и достаточно, чтобы его координаты удовлетворяли соотношениям (4)
(4) ,
,
 – любой вектор, не имеющий асимптотического направления. Так как всегда можно выбрать три неколлинеарных вектора
– любой вектор, не имеющий асимптотического направления. Так как всегда можно выбрать три неколлинеарных вектора  , имеющих относительно поверхности (3) неасимптотическое направление, то однородное относительно
, имеющих относительно поверхности (3) неасимптотическое направление, то однородное относительно  уравнение (5) имеет три линейно независимых решения
уравнение (5) имеет три линейно независимых решения 
 , особых направлений нет.
, особых направлений нет. и система (4) имеет ненулевые решения.
и система (4) имеет ненулевые решения.
 в простейших уравнениях этих поверхностей.
в простейших уравнениях этих поверхностей. равен 1, то система (4) имеет два линейно независимых решения
равен 1, то система (4) имеет два линейно независимых решения  и
и 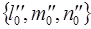 . Все решения системы (4) являются всеми линейными комбинациями этих двух. Это значит, что для поверхностей
. Все решения системы (4) являются всеми линейными комбинациями этих двух. Это значит, что для поверхностей в простейших уравнениях (IV) и (V)).
в простейших уравнениях (IV) и (V)).