|
Лекция 36. Аффинная классификация линий второго порядка.
Определение. Две линии второго порядка принадлежат одному и тому же аффинному классу, если существует аффинное преобразование, переводящее одну из этих линий в другую. Если же одну линию никаким аффинным аффинным преобразованием нельзя перевести в другую, то эти линии принадлежат
различным аффинным классам (линии аффинно неэквивалентны).
Теорема.Все линии второго порядка делятся на 9 аффинных классов:
1. Эллипсы.
2. Мнимые эллипсы.
3. Пары мнимых пересекающихся прямых.
4. Гиперболы.
5. Пары пересекающихся прямых.
6. Параболы.
7. Две параллельные прямые.
8. Две мнимые параллельные прямые.
9. Две совпадающие прямые.
Доказательство.Докажем сначала, что всякие две линии, принадлежащие одному классу, аффинно эквивалентны. Возьмем два любых эллипса на плоскости, и пусть их канонические уравнения (вообще говоря, в разных системах координат) будут
 . .
Производя аффинные сжатия,

к осям  и и  , мы преобразуем эллипс , мы преобразуем эллипс

в эллипс
 . .
Теперь эллипс  совмещается с эллипсом совмещается с эллипсом  движением. Так как аффинные сжатия и движения – аффинные преобразования, то и результирующее преобразование, переводящее второй эллипс в первый, также аффинное. движением. Так как аффинные сжатия и движения – аффинные преобразования, то и результирующее преобразование, переводящее второй эллипс в первый, также аффинное.
Г и п е р б о л а. Доказательство того, что любая гипербола может быть аффинно преобразована в любую другую гиперболу, проводится аналогично.
П а р а б о л а. Рассмотрим две параболы  и и 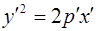 . Произведем преобразование гомотетии . Произведем преобразование гомотетии  . Тогда парабола . Тогда парабола  перейдет в линию перейдет в линию  , или , или  , т.е. снова в параболу, параметр которой равен , т.е. снова в параболу, параметр которой равен 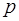 . .
Теперь парабола 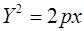 с параболой с параболой  совмещается движением. Таким образом, все параболы не только аффинно эквивалентны, но даже подобны. совмещается движением. Таким образом, все параболы не только аффинно эквивалентны, но даже подобны.
Рассмотрение остальных случаев не представляет затруднений.
Перейдем к доказательству второй части теоремы: всякие две линии, принадлежащие разным классам, аффинно неэквивалентны. Прежде всего заметим, что так как аффинное преобразование выражается линейными соотношениями в координатах, то образ любой линии второго порядка при любом аффинном преобразовании есть линия второго порядка.
Эллипс нельзя преобразовать аффинно ни в одну из других линий, указанных в условии теоремы, так как среди всех линий второго порядка эллипс – единственная линия, лежащая в ограниченной части плоскости и содержащая бесконечное множество точек (действительных). Это свойство множества сохраняется при любом аффинном преобразовании, поэтому образом эллипса при любом аффинном преобразовании будет снова эллипс.
Гипербола от всех остальных линий второго порядка, перечисленных в условии теоремы, отличается тем, что имеет две ветви и не содержит трех точек, лежащих на одной прямой; эти свойства сохраняются при аффинном преобразовании . поэтому аффинным образом гиперболы будет гипербола.
Парабола от всех остальных линий второго порядка, указанных в условии теоремы, отличается тем, что является неограниченной линией, имеющей одну ветвь, и не содержит трех точек, принадлежащих одной прямой; это свойство сохраняется при аффинном преобразовании.
Две пересекающиеся прямые при аффинном преобразовании переходят в две пересекающиеся прямые, а две параллельные прямые – в две параллельные прямые.
Если линия второго порядка распадается на две мнимые пересекающиеся прямые, т.е. на плоскости есть только одна точка, координаты которой удовлетворяют данному уравнению, то после аффинного преобразования образом этой точки будет точка, т.е. образом двух мнимых пересекающихся прямых будут снова две мнимые пересекающиеся прямые.
Мнимый эллипс аффинно неэквивалентен двум мнимым параллельным прямым, так как мнимый эллипс имеет единственный центр. А две мнимые параллельные прямые – прямую центров, а эти свойства сохраняются при любом аффинном преобразовании.
Доказанная теорема позволяет назвать проведенную выше классификацию линий второго порядка аффинной.
Таким образом, аффинной классификацией линий второго порядка является разделение всех линий второго порядка на 9 аффинных классов, в каждый из которых включаются все линии второго порядка, такие, что любые две из них могут быть переведены одна в другую некоторым аффинным преобразованием; если же линии второго порядка принадлежат разным аффинным классам. То никаким аффинным преобразованием одна линия не может быть переведена в другую.
Простейшие представители девяти аффинных классов линий второго порядка таковы:
1) 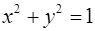 эллипс эллипс
2)  мнимый эллипс мнимый эллипс
3)  две мнимые пересекающиеся прямые две мнимые пересекающиеся прямые
4)  парабола парабола
5)  две действительные пересекающиеся прямые две действительные пересекающиеся прямые
6) 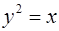 парабола парабола
7)  две параллельные прямые две параллельные прямые
8)  две мнимые параллельные прямые две мнимые параллельные прямые
9)  две совпадающие прямые две совпадающие прямые
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 .
.
 и
и  , мы преобразуем эллипс
, мы преобразуем эллипс
 .
. движением. Так как аффинные сжатия и движения – аффинные преобразования, то и результирующее преобразование, переводящее второй эллипс в первый, также аффинное.
движением. Так как аффинные сжатия и движения – аффинные преобразования, то и результирующее преобразование, переводящее второй эллипс в первый, также аффинное. и
и 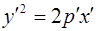 . Произведем преобразование гомотетии
. Произведем преобразование гомотетии  . Тогда парабола
. Тогда парабола  перейдет в линию
перейдет в линию  , или
, или  , т.е. снова в параболу, параметр которой равен
, т.е. снова в параболу, параметр которой равен 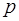 .
.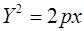 с параболой
с параболой 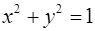 эллипс
эллипс мнимый эллипс
мнимый эллипс две мнимые пересекающиеся прямые
две мнимые пересекающиеся прямые парабола
парабола две действительные пересекающиеся прямые
две действительные пересекающиеся прямые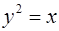 парабола
парабола две параллельные прямые
две параллельные прямые две мнимые параллельные прямые
две мнимые параллельные прямые две совпадающие прямые
две совпадающие прямые