|
Лекция 25. Однополостный гиперболоид и его прямолинейные образующие. Двуполостный гиперболоид.
Введение
Аналитическая геометрия, наряду с математическим анализом и алгеброй, - курс, с изучения которого начинается математическое образование студентов
математиков и механиков. Эти дисциплины составляют фундамент, на котором строится здание математической науки.
Курс аналитической геометрии рассчитан на два семестра. Его назначение - овладение студентами методом геометрических исследований, широко приме-
няемом в других областях естествознания.
Настоящий конспект содержит лекции второго семестра. В нем изложены
теория поверхностей второго порядка, включая их классификацию; линейные и аффинные преобразования; основы проективной геометрии.
Лекция 24. Эллипсоид
Эллипсоидом называется поверхность, уравнение которой в некоторой специально выбранной прямоугольной системе координат имеет вид
 . (1) . (1)
Для эллипсоида (1) начало координат  является его центром симметрии и называется центром эллипсоида; оси координат являются осями симметрии и называются главными осями; плоскости координат являются плоскостями симметрии и называются главными плоскостями. является его центром симметрии и называется центром эллипсоида; оси координат являются осями симметрии и называются главными осями; плоскости координат являются плоскостями симметрии и называются главными плоскостями.
Вершинами трехосного эллипсоида называются точки пересечения эллипсоида с его главными осями. Трехосный эллипсоид имеет шесть вершин
 . .
Из уравнения (1) следует, что  . Это означает, что эллипсоид (1) лежит внутри прямоугольного параллелепипеда с вершинами . Это означает, что эллипсоид (1) лежит внутри прямоугольного параллелепипеда с вершинами
 . Каждая грань этого параллелепипеда имеет с эллипсоидом (1) . Каждая грань этого параллелепипеда имеет с эллипсоидом (1)
только одну общую точку – его вершину.
Плоскость  пересекает эллипсоид (1) по линии, выраженной уравнениями пересекает эллипсоид (1) по линии, выраженной уравнениями  , или эквивалентной системой , или эквивалентной системой
 . (2) . (2)
Аналогично плоскость  пересекает эллипсоид (1) по линии, уравнения которой пересекает эллипсоид (1) по линии, уравнения которой
 , (3) , (3)
а плоскость  по линии по линии
 . (4) . (4)
Линии (2), (3), (4) суть эллипсы. Эти эллипсы, т.е. сечения эллипсоида (1)
его главными плоскостями, называются главными сечениями.
Рассмотрим сечения эллипсоида (1) плоскостями, параллельными какой-ни-
будь координатной плоскости, например плоскостями, параллельными плоскости  , т.е. плоскостями, выражаемыми уравнением , т.е. плоскостями, выражаемыми уравнением 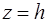 , где , где  – произвольное действительное число. – произвольное действительное число.
Уравнения линии сечения имеют вид
 , , 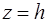 , или , или  , , 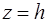 , ,
или  , , 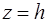 . (5) . (5)
Если  , то первому уравнению этой системы не удовлетворяет ни одна , то первому уравнению этой системы не удовлетворяет ни одна
пара действительных чисел  , т.е. система (5) не имеет действительных решений , т.е. система (5) не имеет действительных решений  . Это означает, что плоскость . Это означает, что плоскость 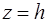 при при  не пересекает эллипсоид (1). не пересекает эллипсоид (1).
При  первое уравнение системы (5) имеет вид первое уравнение системы (5) имеет вид  , откуда , откуда
 . Наконец, если . Наконец, если  , то систему уравнений, выражающих линию сечения, можно переписать так: , то систему уравнений, выражающих линию сечения, можно переписать так:
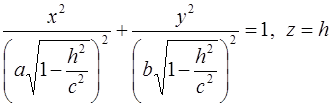 . .
Эти уравнения являются уравнениями эллипса, лежащего в плоскости сече-
ния 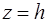 ; центр этого эллипса – точка ; центр этого эллипса – точка  , оси симметрии параллельны осям , оси симметрии параллельны осям  и и 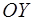 , а полуоси равны , а полуоси равны  . .
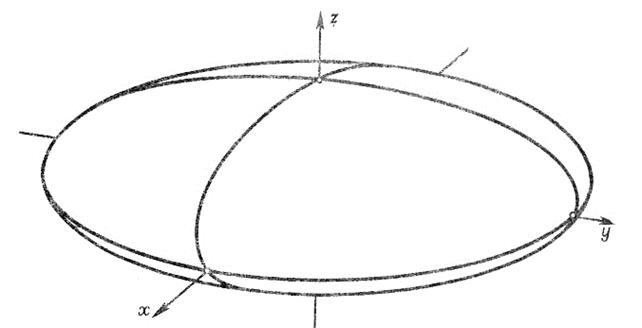
Рис. 1
Рассмотренные сечения дают представление о форме эллипсоида. Отметим, что эллипсоид (1) может быть получен из сферы  , если произвести три равномерных сжатия: , если произвести три равномерных сжатия:

к трем попарно перпендикулярным плоскостям  и и  , проходящим через центр этой сферы. , проходящим через центр этой сферы.
Лекция 25. Однополостный гиперболоид и его прямолинейные образующие. Двуполостный гиперболоид.
Однополостным гиперболоидом называется поверхность, уравнение которой в некоторой специально выбранной прямоугольной системе координат имеет вид
 .(1) .(1)
Для однополостного гиперболоида (1) начало координат является центром симметрии (центр), оси координат – осями симметрии (главные оси), а координатные плоскости – плоскостями симметрии (главные плоскости).
Если в уравнении (1)  , то однополостный гиперболоид (1) называется однополостным гиперболоидом вращения, так как может быть получен вращением гиперболы , то однополостный гиперболоид (1) называется однополостным гиперболоидом вращения, так как может быть получен вращением гиперболы  вокруг ее мнимой оси. вокруг ее мнимой оси.
Вершинами однополостного гиперболоида называются точки пересечения гиперболоида с его главными осями Гиперболоид (1) в случае  имеет четыре вершины имеет четыре вершины  . .
Плоскость  пересекает однополосный гиперболоид (1) по эллипсу, выражаемому уравнениями пересекает однополосный гиперболоид (1) по эллипсу, выражаемому уравнениями  , называемому горловым эллипсом однополостного гиперболоида (1). Плоскость , называемому горловым эллипсом однополостного гиперболоида (1). Плоскость  пересекает однополостный гиперболоид (1) по гиперболе, выражаемой уравнениями пересекает однополостный гиперболоид (1) по гиперболе, выражаемой уравнениями  , а , а
плоскость  – по гиперболе, выражаемой уравнениями – по гиперболе, выражаемой уравнениями  . .
Рассмотрим сечения однополостного гиперболоида (1) плоскостями, параллельными координатной плоскости  , т.е. плоскостями , т.е. плоскостями 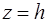 . .
Уравнения линии сечения будут  , , 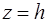 ; эта система уравнений эквивалентна следующей: ; эта система уравнений эквивалентна следующей:  . .
Этими уравнениями выражается эллипс с полуосями
 (2) (2)
с центром на оси  в точке в точке  и осями, параллельными соответственно и осями, параллельными соответственно
осям  и и  . Из выражения (2) следует, что . Из выражения (2) следует, что  , т.е. горловой эллипс является наименьшим из всех эллипсов, по которым однополостный гиперболоид (1) рассекается плоскостями, параллельными плоскости , т.е. горловой эллипс является наименьшим из всех эллипсов, по которым однополостный гиперболоид (1) рассекается плоскостями, параллельными плоскости  . .
Плоскость  , параллельная плоскости , параллельная плоскости  , пересекает однополостный , пересекает однополостный
гиперболоид (1) по линии, выражаемой уравнениями  . .
Если  , то этими уравнениями определяется гипербола с центром в точке , то этими уравнениями определяется гипербола с центром в точке  , лежащая в плоскости , лежащая в плоскости  , действительная ось которой парал- , действительная ось которой парал-
лельна оси  , а мнимая – оси , а мнимая – оси  . Полуоси этой гиперболы: . Полуоси этой гиперболы:
 ( действительная полуось), ( действительная полуось),  (мнимая полуось). (мнимая полуось).
Если  , то уравнения линии сечения имеют вид , то уравнения линии сечения имеют вид  . .
Уравнения  являются уравнениями двух пересекающихся прямых являются уравнениями двух пересекающихся прямых 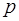 и и  : :
 – прямая – прямая 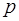 ; ;
 – прямая – прямая  . .
Аналогично, уравнения  являются уравнениями двух являются уравнениями двух
прямых:
 и и  . .
Если  , то в сечении получается гипербола, уравнение которой , то в сечении получается гипербола, уравнение которой
 . .
Действительная ось этой гиперболы параллельна оси  , мнимая – оси , мнимая – оси  ; ;
центр лежит в точке  . .
Асимптоты всех гипербол, получающихся при пересечении однополостного гиперболоида (1) плоскостями  , параллельны прямым, получающимся при пересечении гиперболоида плоскостями , параллельны прямым, получающимся при пересечении гиперболоида плоскостями  . .
Сечения плоскостями  , параллельными плоскости , параллельными плоскости  , аналогичны , аналогичны
рассмотренным.
Все эти сечения дают представление о форме поверхности однополостного
гиперболоида (рис. 2).

Рис. 2
Определение. Прямая, все точки которой лежат на поверхности второго
порядка, называется прямолинейной образующей этой поверхности.
Теорема 1. Через каждую точку однополостного гиперболоида проходят
две и только две его прямолинейные образующие.
Множество образующих определяется уравнениями:
 и и  , ,
где  – координаты точки горлового эллипса. – координаты точки горлового эллипса.
Двуполостным гиперболоидом называется поверхность, уравнение которой в некоторой специально выбранной прямоугольной системе координат имеет вид
 . (3) . (3)
Начало координат является центром симметрии (центр) двуполостного гиперболоида, оси координат – осями симметрии (главные оси), координатные плоскости – плоскостями симметрии (главные плоскости).
Вершинами двуполостного гиперболоида называются точки его пересечения с главной осью  . Двуполостный гиперболоид (1) имеет две вершины . Двуполостный гиперболоид (1) имеет две вершины  . .
Плоскости  и и  пересекают двуполостный гиперболоид (3) по гиперболам пересекают двуполостный гиперболоид (3) по гиперболам 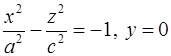 и и  . .
Сечение двуполостного гиперболоида плоскостью 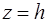 выражается уравнениями выражается уравнениями  . .
Если  , то первое уравнение не имеет действительных решений – плоскость , то первое уравнение не имеет действительных решений – плоскость 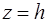 не пересекает поверхности. не пересекает поверхности.
Если  , то , то  , откуда , откуда  , плоскости , плоскости  встречают поверхность двуполостного гиперболоида в его вершинах встречают поверхность двуполостного гиперболоида в его вершинах  . Если . Если
 , то уравнения линии сечения можно переписать в виде , то уравнения линии сечения можно переписать в виде
 . .
Этими уравнениями выражается эллипс с полуосями  , ,  с центром в точке с центром в точке  и осями, соответственно параллельными осям и осями, соответственно параллельными осям  и и  . .
Плоскость  пересекает поверхность двуполостного гиперболоида по пересекает поверхность двуполостного гиперболоида по
линии, выражаемой уравнениями  , или , или
 , ,
т.е. по гиперболе с центром в точке  , лежащей в плоскости , лежащей в плоскости  . Действительная ось этой гиперболы параллельна оси . Действительная ось этой гиперболы параллельна оси  , мнимая – оси , мнимая – оси  . .
Аналогично исследуются сечения поверхности плоскостями  (рис.3). (рис.3).

Рис. 3
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 . (1)
. (1) является его центром симметрии и называется центром эллипсоида; оси координат являются осями симметрии и называются главными осями; плоскости координат являются плоскостями симметрии и называются главными плоскостями.
является его центром симметрии и называется центром эллипсоида; оси координат являются осями симметрии и называются главными осями; плоскости координат являются плоскостями симметрии и называются главными плоскостями.  .
. . Это означает, что эллипсоид (1) лежит внутри прямоугольного параллелепипеда с вершинами
. Это означает, что эллипсоид (1) лежит внутри прямоугольного параллелепипеда с вершинами . Каждая грань этого параллелепипеда имеет с эллипсоидом (1)
. Каждая грань этого параллелепипеда имеет с эллипсоидом (1) пересекает эллипсоид (1) по линии, выраженной уравнениями
пересекает эллипсоид (1) по линии, выраженной уравнениями  , или эквивалентной системой
, или эквивалентной системой . (2)
. (2) пересекает эллипсоид (1) по линии, уравнения которой
пересекает эллипсоид (1) по линии, уравнения которой , (3)
, (3)  по линии
по линии . (4)
. (4) , т.е. плоскостями, выражаемыми уравнением
, т.е. плоскостями, выражаемыми уравнением 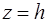 , где
, где  – произвольное действительное число.
– произвольное действительное число. ,
,  ,
,  , то первому уравнению этой системы не удовлетворяет ни одна
, то первому уравнению этой системы не удовлетворяет ни одна , т.е. система (5) не имеет действительных решений
, т.е. система (5) не имеет действительных решений  . Это означает, что плоскость
. Это означает, что плоскость  первое уравнение системы (5) имеет вид
первое уравнение системы (5) имеет вид  , откуда
, откуда . Наконец, если
. Наконец, если  , то систему уравнений, выражающих линию сечения, можно переписать так:
, то систему уравнений, выражающих линию сечения, можно переписать так: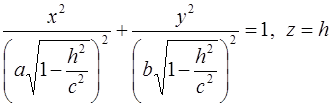 .
.  , оси симметрии параллельны осям
, оси симметрии параллельны осям  и
и 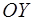 , а полуоси равны
, а полуоси равны  .
. 
 , если произвести три равномерных сжатия:
, если произвести три равномерных сжатия:
 и
и  .(1)
.(1) , то однополостный гиперболоид (1) называется однополостным гиперболоидом вращения, так как может быть получен вращением гиперболы
, то однополостный гиперболоид (1) называется однополостным гиперболоидом вращения, так как может быть получен вращением гиперболы  вокруг ее мнимой оси.
вокруг ее мнимой оси. имеет четыре вершины
имеет четыре вершины  .
. , называемому горловым эллипсом однополостного гиперболоида (1). Плоскость
, называемому горловым эллипсом однополостного гиперболоида (1). Плоскость  , а
, а – по гиперболе, выражаемой уравнениями
– по гиперболе, выражаемой уравнениями  .
. .
. (2)
(2) в точке
в точке  и
и  . Из выражения (2) следует, что
. Из выражения (2) следует, что  , т.е. горловой эллипс является наименьшим из всех эллипсов, по которым однополостный гиперболоид (1) рассекается плоскостями, параллельными плоскости
, т.е. горловой эллипс является наименьшим из всех эллипсов, по которым однополостный гиперболоид (1) рассекается плоскостями, параллельными плоскости  , параллельная плоскости
, параллельная плоскости  .
. , то этими уравнениями определяется гипербола с центром в точке
, то этими уравнениями определяется гипербола с центром в точке  , лежащая в плоскости
, лежащая в плоскости  ( действительная полуось),
( действительная полуось),  (мнимая полуось).
(мнимая полуось). , то уравнения линии сечения имеют вид
, то уравнения линии сечения имеют вид  .
. являются уравнениями двух пересекающихся прямых
являются уравнениями двух пересекающихся прямых 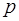 и
и  :
: – прямая
– прямая  – прямая
– прямая  являются уравнениями двух
являются уравнениями двух и
и  .
. , то в сечении получается гипербола, уравнение которой
, то в сечении получается гипербола, уравнение которой .
. , параллельны прямым, получающимся при пересечении гиперболоида плоскостями
, параллельны прямым, получающимся при пересечении гиперболоида плоскостями  .
. , параллельными плоскости
, параллельными плоскости 
 и
и  ,
, – координаты точки горлового эллипса.
– координаты точки горлового эллипса. . (3)
. (3) .
.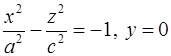 и
и  .
. .
. встречают поверхность двуполостного гиперболоида в его вершинах
встречают поверхность двуполостного гиперболоида в его вершинах  .
.  ,
,  с центром в точке
с центром в точке  , или
, или ,
,