|
Лекция 33. Аффинные преобразования плоскости и пространства; определение и основные свойства.
Линейное точечное преобразование пространства ( плоскости или прямой) называется аффинным, если оно взаимно однозначно.
Линейное точечное отображение плоскости на плоскость или прямой на прямую называется аффинным, если оно взаимно однозначно.
Линейное преобразование пространства будет взаимно однозначным, т.е. аффинным тогда и только тогда, когда при этом преобразовании какие-нибудь три некомпланарных вектора переходят снова в некомпланарные векторы.
Замечание. Если преобразование пространства аффинное, то оно любую тройку некомпланарных векторов переводит в некомпланарную тройку.
Аффинное отображение плоскости  на плоскость на плоскость  ( и аффинное преобразование пространства) можно определить как такое взаимно однозначное отображение плоскости ( и аффинное преобразование пространства) можно определить как такое взаимно однозначное отображение плоскости  на плоскость на плоскость  , при котором три любые точки плоскости , при котором три любые точки плоскости  , принадлежащие одной прямой, отображаются в три точки плоскости , принадлежащие одной прямой, отображаются в три точки плоскости  , также принадлежащие одной прямой. , также принадлежащие одной прямой.
Теорема 1. При аффинном отображении  плоскости плоскости  на плоскость на плоскость
 множество всех точек произвольной прямой множество всех точек произвольной прямой  , лежащей на плоскость , лежащей на плоскость  , ,
отображается и притом взаимно однозначно на множество всех точек некоторой прямой  , лежащей на плоскости , лежащей на плоскости  . .
Прямая  называется образом прямой называется образом прямой  , а прямая , а прямая  – прообразом прямой – прообразом прямой 
при аффинном отображении  . .
Теорема 2.При аффинном отображении  плоскости плоскости  на плоскость на плоскость  образы образы  и и  параллельных прямых параллельных прямых 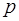 и и  суть параллельные прямые, а образы суть параллельные прямые, а образы  и и  пересекающихся прямых пересекающихся прямых 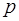 и и  суть пересекающиеся прямые; при этом точка суть пересекающиеся прямые; при этом точка  пересечения прямых пересечения прямых  и и  является образом точки является образом точки  пересечения прямых пересечения прямых 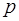 и и  . .
Теорема 3. При аффинном отображении  плоскости плоскости  на плоскость на плоскость
 середина середина  произвольного отрезка произвольного отрезка  переходит в середину переходит в середину  отрезка отрезка
 ( (  и и  – образы точек – образы точек  и и  при отображении при отображении  ). ).
Теорема 4. Если разделить отрезок  на на  равных частей равных частей
 то то 
где  – образы точек – образы точек  при аффинном отображении при аффинном отображении  плоскости плоскости  на плоскость на плоскость  . .
Из этой теоремы следует, что если точка  делит направленный отрезок делит направленный отрезок
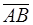 в рациональном отношении в рациональном отношении  , то образ , то образ  точки точки  при аффинном отображении при аффинном отображении  плоскости плоскости  на плоскость на плоскость  делит отрезок делит отрезок  в том же отношении в том же отношении  . .
Теорема 5. (Дарбу)Рассмотрим аффинное отображение  плоскости плоскости
 на плоскость на плоскость  . Пусть . Пусть  – произвольный отрезок, лежащий на плоскости – произвольный отрезок, лежащий на плоскости  , а , а  – какая-нибудь точка прямой – какая-нибудь точка прямой  . Тогда образ . Тогда образ  точки точки  при отображении при отображении  является внешней точкой для отрезка является внешней точкой для отрезка  , где , где  и и  – –
образы точек  и и  при отображении при отображении  . .
Теорема 6. При аффинном отображении  плоскости плоскости  на плоскость на плоскость  сохраняется простое отношение трех точек, принадлежащих одной прямой. сохраняется простое отношение трех точек, принадлежащих одной прямой.
Таким образом, аффинное отображение является линейным.
Свойства аффинных преобразований и отображений
Теорема 7.Произведение двух аффинных преобразований есть снова аффинное преобразование.
Доказательство. Пусть  и и  – два аффинных преобразования. Рассмотрим три произвольные точки – два аффинных преобразования. Рассмотрим три произвольные точки  и и  , принадлежащие одной прямой, и пусть , принадлежащие одной прямой, и пусть
 – образы точек – образы точек  при аффинном преобразовании при аффинном преобразовании  . .
Так как точки  принадлежат одной прямой, то существует такое число принадлежат одной прямой, то существует такое число  , что , что  , но тогда в силу линейности отображения , но тогда в силу линейности отображения 
 , значит (в силу того, что , значит (в силу того, что  также линейное преобразование) также линейное преобразование)
 . Таким образом, произведение . Таким образом, произведение  есть линейное преобразование. К тому же оно и взаимно однозначно (ибо произведение двух любых взаимно однозначных преобразований есть взаимно однозначное преобразование), следовательно, есть линейное преобразование. К тому же оно и взаимно однозначно (ибо произведение двух любых взаимно однозначных преобразований есть взаимно однозначное преобразование), следовательно,  – аффинное преобразование. – аффинное преобразование.
Теорема 8.Преобразование  , обратное к аффинному преобразованию, также является аффинным. , обратное к аффинному преобразованию, также является аффинным.
Доказательство. Пусть  – три произвольные точки, принадлежащие одной прямой и связанные соотношением – три произвольные точки, принадлежащие одной прямой и связанные соотношением  ; докажем, что ; докажем, что
тем же соотношением будут связаны их прообразы при аффинном преобразовании  . .
В самом деле, пусть  и и  – прообразы точек – прообразы точек  и и  . Построим точку . Построим точку  , ,
такую, что  . Пусть . Пусть  – образ точки – образ точки  при аффинном преобразовании при аффинном преобразовании  . Тогда . Тогда  . Значит, . Значит,  , т.е. точка , т.е. точка  совпадает с точкой совпадает с точкой  , поэтому , поэтому  – прообраз – прообраз  . Кроме того, ясно, что . Кроме того, ясно, что  взаимно однозначное преобразование (так как преобразование, обратное любому взаимно однозначному преобразованию, снова взаимно однозначно). взаимно однозначное преобразование (так как преобразование, обратное любому взаимно однозначному преобразованию, снова взаимно однозначно).
Следствие. Из теорем 7 и 8 следует, что множество всех аффинных преобразований пространства образует группу.
Точно так же доказывается, что множество всех аффинных преобразований плоскости образует группу так же, как и множество всех аффинных преобразо
ваний прямой образует группу.
Теорема 9. При аффинном преобразовании пространства
1) две параллельные плоскости переходят в две параллельные плоскости:
2) две пересекающиеся плоскости  и и  переходят в две пересекающиеся плоскости переходят в две пересекающиеся плоскости  и и  ; образом прямой ; образом прямой  , по которой пересекаются плоскости , по которой пересекаются плоскости  и и  , является прямая , является прямая  пересечения плоскостей пересечения плоскостей  и и  ; при этом отображение прямой ; при этом отображение прямой  на прямую на прямую  – аффинное; – аффинное;
3) две параллельные прямые переходят в две параллельные прямые;
4) две пересекающиеся прямые 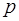 и и  переходят в две пересекающиеся прямые переходят в две пересекающиеся прямые  и и  , причем образом точки , причем образом точки  пересечения прямых пересечения прямых 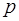 и и  является точка является точка  пересечения прямых пересечения прямых  и и  ; ;
5) две скрещивающиеся прямые переходят в две скрещивающиеся прямые;
6) если прямая 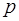 параллельна плоскости параллельна плоскости  , то и прямая , то и прямая  , являющаяся образом прямой , являющаяся образом прямой 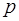 , параллельна плоскости , параллельна плоскости  , в которую переходит плоскость , в которую переходит плоскость
 при данном аффинном преобразовании; при данном аффинном преобразовании;
7) если прямая 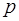 и плоскость и плоскость  пересекаются, то пересекаются прямая пересекаются, то пересекаются прямая  и плоскость и плоскость  , являющиеся их образами, причем точка пересечения , являющиеся их образами, причем точка пересечения  является образом точки является образом точки  пересечения прямой пересечения прямой 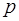 и плоскости и плоскости  . .
Теорема 10.Существует и притом только одно аффинное преобразование пространства, которое любые четыре точки  , не лежащие в одной плоскости, переводит в произвольные четыре точки , не лежащие в одной плоскости, переводит в произвольные четыре точки  , также не лежащие в одной плоскости. , также не лежащие в одной плоскости.
Следствие. Аффинное преобразование пространства, которое оставляет неподвижными четыре точки, не лежащие в одной плоскости, есть тождественное преобразование.
Замечание. Аффинное отображение плоскости на плоскость или аффинное преобразование плоскости определяется и притом однозначно соответствием двух неколлинеарных троек точек.
Аффинное отображение прямой на прямую или аффинное преобразование прямой определяется и притом однозначно заданием двух пар соответственных точек.
Аффинные преобразования в координатах
Пусть даны два аффинных преобразования пространства  и и  относительно общей декартовой системы координат: относительно общей декартовой системы координат:
  ( (  ) )
и
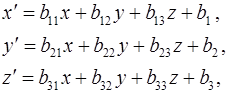  . ( . (  ) )
Преобразование  переводит точку переводит точку  в точку в точку  , определяемую формулами ( , определяемую формулами (  ), а преобразование ), а преобразование  точку точку  переводит в точку переводит в точку  с координатами с координатами

Значит, мы получим преобразование  в координатах, если в последние формулы вместо в координатах, если в последние формулы вместо  подставим их выражения из формул подставим их выражения из формул  ; сделав это, получим ; сделав это, получим
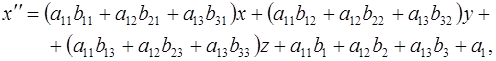
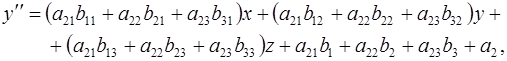
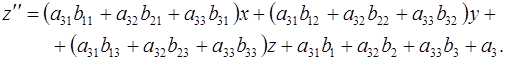
Отметим, что матрица  преобразования преобразования  равна произведению матрицы равна произведению матрицы  преобразования преобразования  на матрицу на матрицу  преобразования преобразования  : :  . .
Отсюда  , и так как , и так как 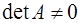 и и  , то и , то и  . Мы еще раз доказали теорему о том, что произведение двух аффинных преобразований есть аффинное преобразование. . Мы еще раз доказали теорему о том, что произведение двух аффинных преобразований есть аффинное преобразование.
Заменяя в соотношениях 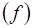  соответственно на соответственно на  , а , а 
соответственно на  и разрешая затем полученные соотношения относительно и разрешая затем полученные соотношения относительно  , получим формулы, дающие в координатах преобразование , получим формулы, дающие в координатах преобразование  , обратное , обратное  : :
 (1) (1)
Матрица  этого линейного преобразования есть матрица, обратная этого линейного преобразования есть матрица, обратная
для матрицы  аффинного преобразования аффинного преобразования  и поэтому и поэтому  . .
Следовательно, формулами (1) дается аффинное преобразование.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 на плоскость
на плоскость  ( и аффинное преобразование пространства) можно определить как такое взаимно однозначное отображение плоскости
( и аффинное преобразование пространства) можно определить как такое взаимно однозначное отображение плоскости  плоскости
плоскости  , лежащей на плоскость
, лежащей на плоскость  , лежащей на плоскости
, лежащей на плоскости  и
и  параллельных прямых
параллельных прямых 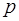 и
и  суть параллельные прямые, а образы
суть параллельные прямые, а образы  пересечения прямых
пересечения прямых  пересечения прямых
пересечения прямых  произвольного отрезка
произвольного отрезка  переходит в середину
переходит в середину  отрезка
отрезка (
(  и
и  – образы точек
– образы точек  и
и  при отображении
при отображении  равных частей
равных частей  то
то 
 – образы точек
– образы точек  при аффинном отображении
при аффинном отображении  делит направленный отрезок
делит направленный отрезок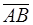 в рациональном отношении
в рациональном отношении  , то образ
, то образ  точки
точки  в том же отношении
в том же отношении  и
и  – два аффинных преобразования. Рассмотрим три произвольные точки
– два аффинных преобразования. Рассмотрим три произвольные точки  и
и  – образы точек
– образы точек  при аффинном преобразовании
при аффинном преобразовании  , но тогда в силу линейности отображения
, но тогда в силу линейности отображения  , значит (в силу того, что
, значит (в силу того, что  . Таким образом, произведение
. Таким образом, произведение  есть линейное преобразование. К тому же оно и взаимно однозначно (ибо произведение двух любых взаимно однозначных преобразований есть взаимно однозначное преобразование), следовательно,
есть линейное преобразование. К тому же оно и взаимно однозначно (ибо произведение двух любых взаимно однозначных преобразований есть взаимно однозначное преобразование), следовательно,  , обратное к аффинному преобразованию, также является аффинным.
, обратное к аффинному преобразованию, также является аффинным. – образ точки
– образ точки  . Значит,
. Значит,  , т.е. точка
, т.е. точка  и
и  переходят в две пересекающиеся плоскости
переходят в две пересекающиеся плоскости  и
и  ; образом прямой
; образом прямой  , по которой пересекаются плоскости
, по которой пересекаются плоскости  пересечения плоскостей
пересечения плоскостей  , в которую переходит плоскость
, в которую переходит плоскость  , не лежащие в одной плоскости, переводит в произвольные четыре точки
, не лежащие в одной плоскости, переводит в произвольные четыре точки  , также не лежащие в одной плоскости.
, также не лежащие в одной плоскости.
 (
( 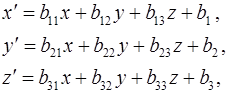
 . (
. (  в точку
в точку  , определяемую формулами (
, определяемую формулами (  с координатами
с координатами
 в координатах, если в последние формулы вместо
в координатах, если в последние формулы вместо  подставим их выражения из формул
подставим их выражения из формул  ; сделав это, получим
; сделав это, получим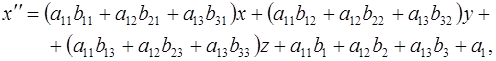
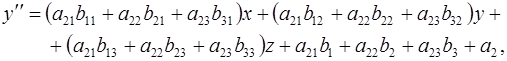
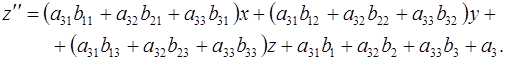
 .
. , и так как
, и так как 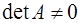 и
и  , то и
, то и  . Мы еще раз доказали теорему о том, что произведение двух аффинных преобразований есть аффинное преобразование.
. Мы еще раз доказали теорему о том, что произведение двух аффинных преобразований есть аффинное преобразование.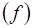
 соответственно на
соответственно на  , а
, а  (1)
(1) этого линейного преобразования есть матрица, обратная
этого линейного преобразования есть матрица, обратная