
|
|
Электропроводность растворов электролитовПри отсутствии внешнего электрического поля ионы в растворах электролитов беспорядочно перемещаются по всем направлениям. При подключении внешнего источника тока начинает преобладать одно из направлений перемещения ионов согласно знакам из зарядов. В общем случае электропроводность W — величина, обратная электрическому сопротивлению R , в системе СИ имеет размерность Ом-1. Для измерения электропроводности различных растворов необходимо иметь электрохимическую ячейку, которая состоит из двух проводников первого рода, погруженных в раствор электролита (проводник второго рода) и соединенных с внешним источником тока. Удельная электропроводность раствора определяется как величина, обратная удельному электрическому сопротивлению æ = где æ — удельная электропроводность, Ом-1, м-1 ; R — сопротивление, Oм; S — площадь поперечного сечения проводника, м2 ; l – длина проводника, м. Таким образом, удельная электропроводность æ представляет собой количество электричества, которое проходит через поперечное сечение электролита площадью 1 см2 зa 1 c при приложенном внешнем напряжении 1 B и расстоянии между электродами 1 см, т.е. это – электропроводность одного кубического сантиметра электролита. Скорость движения иона в электрическом поле определяется как величина пути его направленного перемещения к одному из электродов и выражается в системе СИ в м/с. Зависимость удельной электропроводности от концентрации раствора электролита показана на рис. 2.2. Эта зависимость представлена кривыми с максимумом. Такой ход кривых легко объяснить, исходя из следующих рассуждений. На начальном участке кривой с ростом концентрации раствора удельная электропроводность растворов электролитов возрастает. Это закономерно, так как электрический ток в проводниках второго рода обеспечивается за счет движения ионов, и чем их больше, тем выше электропроводность.
Рис. 2.2. Зависимость удельной электропроводности от концентрации раствора
Однако по мере дальнейшего роста концентрации раствора расстояние между ионами будет уменьшаться и, как следствие, усиливаться взаимодействие между ними, что будет тормозить движение ионов. Поэтому увеличение концентрации раствора после некоторого предела закономерно приведет к уменьшению электропроводности. С ростом температуры удельная электропроводность возрастает, что объясняется уменьшением вязкости раствора и степени гидратации ионов, а также увеличением степени диссоциации электролита. В технических расчетах чаще всего пользуются величиной эквивалентной электропроводности. Она обозначается буквой λ и представляет собой количество электричества, протекающее за 1 с по столбику жидкости высотой 1 см и имеющее такое сечение, чтобы в его объеме поместился раствор, содержащий один г-эквивалент растворенного вещества. Падение напряжения на этом столбике должно составлять 1 В. Для разбавленных растворов эта площадь чрезвычайно велика (например, для 0,01 н раствора она должна быть равной 100 000 см2). Для расчета λ, следовательно, необходимо рассчитать число ячеек площадью 1 см2. Так, для 0,01 н раствора объем, содержащий один эквивалент вещества, будет равен V =
ячеек ( Отсюда λ = (æ/N)∙ I000 см2/г-экв ∙Ом, (2.43) где N – нормальность раствора. Обычно на практике измеряют значение удельной электропроводности и по нему рассчитывают эквивалентную электропроводность растворов электролитов.
Если использовать величину V, обозначающую разбавление (или – разведение) раствора, то λ = æ∙V∙I000 см2/г-экв∙ Ом. (2.44) Эквивалентная электропроводность как сильных, так и слабых электролитов увеличивается с ростом разведения и достигает предельной величины, которая называется эквивалентной электропроводностью при бесконечном разведении λ∞ (рис. 2.3). Эта закономерность для растворов слабых электролитов объясняется тем, что процесс диссоциации слабого электролита на ионы с увеличением разбавления может происходить до конца, так как с увеличением разбавления раствора расстояние между частицами растворенного вещества растет и число частиц, распавшихся на ионы, преобладает над количеством недиссоциированных молекул. Поэтому доля распавшихся молекул растворенного вещества в объеме, содержащем его один г-эквивалент, увеличивается. Это приводит к увеличению числа переносчиков электричества, и эквивалентная электропроводность возрастает. Такойрост будет происходитьдо тех пор, пока все молекулы растворенного вещества не распадутся на ионы (α = I). Строго говоря, это возможно лишь при бесконечном разведении. Такая электропроводность и обозначается λ∞. Следовательно, отношение электропроводностей раствора электролита при данном и бесконечном разведении будет определять степень его диссоциации
Так как электропроводность возникает за счет независимого движения катионов и анионов, то λ = λ+ + λ- , (2.46) где λ+ — электропроводность, обусловленная катионами, а λ- — анионами. λ+ и λ- называют также подвижностью катиона и аниона. Она пропорциональна скорости движения иона V: λ+ = V+ . F ; ,λ- = V- F, где F — число Фарадея. Для бесконечно разбавленного раствора
Это соотношение выражает собой закон аддитивности электропроводностей Кольрауша. Величины Возрастание эквивалентной электропроводности с разбавлением раствора (рис. 2.4) для сильных электролитов объясняется тем, что в разбавленных растворах из-за уменьшения межионного взаимодействия, тормозящего движение ионов, облегчается перемещение ионов по всему объему. Для разбавленных растворов сильных электролитов с концентрацией С < 2∙1O-3 г-экв/л эквивалентная электропроводность зависит от концентрации по уравнению λ = λ∞ — А где A — постоянный множитель, зависящий от свойств растворителя. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 :
: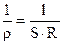 , (2.42)
, (2.42)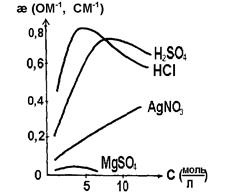
 = 100 л (он называется разведением), или 100 000 см3. Поэтому в площади столбика жидкости высотой 1 см уместится 10 000 таких
= 100 л (он называется разведением), или 100 000 см3. Поэтому в площади столбика жидкости высотой 1 см уместится 10 000 таких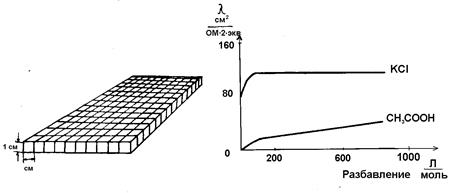
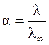 . (2.45)
. (2.45)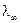 =
=  . (2.47)
. (2.47) для различных ионов приводятся в справочниках.
для различных ионов приводятся в справочниках.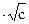 , (2.48)
, (2.48)