
|
|
Цепные (лестничные) схемы. ( Схема Кауэра ).
Запишем Z(P) и Y(P) соответственно для первой и второй схем. 1. ЗАДАЧА
Найдем Z, K=L1 тогда, Пусть задано Z(P) выясним, что удовлетворяет ли оно критериям физической реализуемости , и преобразуем его формуле Кауэра Запишем полиномы A(P) и B(P) по убывающим степеням. Последовательно делим числитель и знаменатель с понижением степени переменной, так чтобы в конце получился 0. Получаем что степень числителя больше степени знаменателя.
Пример второй реализации в книге Шебест «ТЛЭЦ». Для второго случая. Если в аналитическом выражении Z(P) старшая степень полинома «В» выше старшей Степени полинома «А», то первое деление будет
Если в аналитическом выражении Ζ(p) старшая степень полимера B выше старшей степени полинома A, то первое деление B/A и результат первого деления будет Y1 и схема будет так:
Вывод: цепные схемы достаточно сложны для написания аналитического выражения Ζ и вычисления значения резонансных частот, но они очень удобны для синтеза схем двухполюсника по заданному аналитическому выражению. Задача: преобразовать эту параллельно каноническую схему в цепную по первой реализации по Кауэру. Z(P)=(pL1+ 2) 2p4+3p2+1 3p3+2p - 2p4+4/3p2 2/3p=Z 5/3p2+1=M1
2)3p3+2p 5/3p2+1 - 3p3+9/5p 9/5p=Y1 1/5p=N1
3) - 5/3p2 25/3p=Z2 1=M2 4)1/5p 1 - 1/5 1/5p=Y2 Рисуем схему по данным вычислений Эта схема эквивалентна заданной, частотные характеристики одинаковы и резонансы совпадают. Вторая реализация по Кауэру 1+3p2+2p4
Примечание: Если в заданной функции Z(p) степень числителя выше степени знаменателя, то реализацию по Кауэру производят путем деления числителя на знаменатель Если степень знаменателя выше чем степень числителя, о реализацию производят делением знаменателя на числитель. При этом приходят к следующим формулам.
Сокращаемые» элементы двухполюсников.
– такие элементы, добавление которых в схему не изменяет числа резонансов схемы. Выявить являются те или иные элементы сокращаемыми или нет можно двумя способами: 1). Написать аналитическое выражение Z(P) или Z(ω) приравнять числитель(найдем резонанс напряжений) и знаменатель (найдем резонанс токов), т.е. выяснить число резонансов и сравнить с числом элементов.
2). Графически построить зависимость сопротивления от частоты, выяснить число резонансов и сравнить с числом элементов.
Пример:
Возникло подозрение не являются ли элементы L3 и C3 сокращаемыми. Построим график.
Из графика видно, что он дважды пересекает ось Z=0, т.е. имеет два резонансанапряжений и один резонанс токов. Данную схему можно представить в виде схемы имеющей 4 элемента.
Добавление L13, C3 не изменило общего числа резонансов, а привело к сдвигу резонансов напряжений. ПРИМЕР: Число резонанса получилось n-3, где n – число элементов схемы, это значит, что два элемента будут сокращаемыми.
Двухполюсник с потерями.
При Z=R+jX придется рисовать два графика: фазовый и сопротивлений. Цепи первого порядка (одноэлементный двухполюсник)
Основной характеристикой двухполюсника является частотная характеристика. Частотную характеристик можно представить в двух системах координат: комплексной и полярной системах координат.
Двухэлементные двухполюсники с потерями. Здесь возможен резонанс. r-может быть потерями или непосредственно активное сопротивление, которое напаяны в схему. Ζ1=r+j(ωL – Z=√r2+(ωL – Z=arctg ωL-
Z1
wрез.
Резонанс Zm(Z1)=0 ωрез1=
2) Y2=
Ym(Y2)=-
-L-ωрез2C2 L r22+ r12C+ ωрез2L2 C=0
ωрез=
резонанс возможен в следующей ситуации 4 C>r12 4 C>r12 L/C> r22 L/C> r22
L/C > r12 L/C> r12 L/C<r22L/C<r22 Вывод: таким образом в параллельном контуре с потерями 5) Не всегда есть резонанс токов 6) Резонансная частота зависит не только от величин активных сопротивлений, но и от сопротивления потерь r(R) 7) Часто используют контура с очень малыми потерями 8) 4 C>>r12 (r22) ωрез = Но стабильность настройки контура (неизменность резонансной частоты) зависит не только от стабильности L и C, но и от стабильности потерь r1,r2.Поэтому в цепях (схемах), где нужно иметь очень стабильную частоту, контур определяющий стабильность работы устройств не должен непосредственно нагружаться, а нагрузка включается через каскад.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 2.
2. 

 .
.


 и результат первого деления будет Y1 и схема будет выглядеть следующим образом:
и результат первого деления будет Y1 и схема будет выглядеть следующим образом:  )
)  +
+ 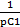 +pL2+
+pL2+ 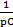 =
=  =2p4+3p2+
=2p4+3p2+  +2p=
+2p=  – cтепень отличается не больше, чем на 1; коэффициенты положительны, для реактивного двухполюсника один из многочленов является с четными степенями, другой с нечетными.
– cтепень отличается не больше, чем на 1; коэффициенты положительны, для реактивного двухполюсника один из многочленов является с четными степенями, другой с нечетными. +1 1/5
+1 1/5 (4.24)
(4.24) ;
; 

 ;
;
 )
)
 ωрез =
ωрез = 
 +jωL+
+jωL+  +
+  =
= 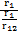 +ω2L2+
+ω2L2+ 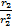 +
+  +ω2L2+
+ω2L2+  =Re(Y2)
=Re(Y2) +ωрез2L2 +
+ωрез2L2 + 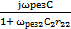 = 0
= 0 =
= 