
|
|
Уточнение понятия алгоритмаМашина с неограниченными регистрами является исполнителем, представляющим собой простой "идеализированный компьютер". Идеализация состоит в том, что каждый отдельный реальный компьютер ограничен как величиной чисел, которые поступают на вход, так и размером памяти (необходимой для запоминания промежуточных результатов), МНР лишена этих ограничений. Машина с неограниченными регистрами имеет неограниченно большую память, ячейки которой будем называть регистрами и обозначать R1, R2, R3,…. Каждый регистр в любой момент времени содержит неотрицательное целое число.
Рис. 3.1. Регистры МНР При этом только конечное множество регистров содержит числа, отличные от нуля. Все остальные регистры заполнены нулями. Это допущение предполагает, что каждый алгоритм использует только конечный объем памяти. В список предписаний МНР входит четыре команды: команда обнуления Z(n); команда прибавления единицы S(n); команда переадресации T(m, n) и команда условного переходам J(m, n, q). Команды обнуления, прибавления единицы и переадресации называются арифметическими.
Рис. 3.2. Список предписаний МНР Алгоритмом называется конечная непустая последовательность команд из списка предписаний МНР, начинающаяся с команды с номером 1. Производя вычисления по данному алгоритму, МНР изменяет содержимое регистров памяти в точном соответствии с командами алгоритма. Исходное состояние памяти, то есть последовательность чисел Предположим, что некоторый алгоритм P состоит из последовательности команд I1, I2, ..., Is. МНР начинает вычисление с команды I1, затем выполняются команды I2, I3 и т. д. до тех пор, пока не встретится команда вида J(m, n, q). В этом случае МНР переходит к выполнению команды, предписанной J(m, n, q) и текущим содержанием регистров Rm и Rn. МНР выполняет алгоритм P: I1, I2, ..., Is до тех пор, пока это возможно. Вычисление останавливается тогда и только тогда, когда нет следующей команды, то есть когда МНР только что выполнила команду Ik и следующая команда в вычислении есть Iv, где v > s. Это может произойти одним из способов: I) если Ik = Is (выполнена последняя команда в P) и Ik - арифметическая команда; 2) если Ik = J(m, n, q), Rm = Rn и q > s. 3) если Ik = J(m, n, q), Rm Rn и q = s. В этом случае будем говорить, что вычисление остановилось после выполнения команды Ik, и заключительная конфигурации есть последовательность r1, r2, r3, ... содержимого регистров на этом шаге. Результатом применения алгоритма к некоторой начальной конфигурации будем считать число r1 из регистра R1 заключительной конфигурации. Бывают, конечно, вычисления, которые никогда не заканчиваются. В случае, если вычислительный процесс не заканчивается получением результата, говорят, что алгоритм неприменим к начальной конфигурации. Пример 3.1. Рассмотрим алгоритм P1
Применим алгоритм к следующей начальной конфигурации:
Рис. 3.3. Начальная конфигурация Ход вычисления на МНР по алгоритму P1 с начальной конфигурацией, изображенной на рисунке 3.3, можно представить, записывая последовательно сверху вниз конфигурации машины вместе со следующей командой, к которой она переходит на данном шаге.
Рис. 3.4. Вычисление по алгоритму P1
Определение 3.1. Пусть f - функция от n неотрицательных целыхпеременных со значениями во множестве Z0 неотрицательных целых чисел(функция 1) вычисление P(a1, a2, ..., an) останавливается тогда и только тогда, когда (a1, a2, ..., an) принадлежит области определения f; 2) если (a1, a2, ..., an) принадлежит области определения f; то в заключительной конфигурации в регистре R1 находится целое число b такое, что f(a1, a2, ..., an) = b. С этого момента под термином вычислимое будем подразумевать МНР-вычислимое. Рассмотрим теперь несколько простых примеров вычислимых функций. Пример 3.2. Докажите МНР-вычислимость функции x + y. Решение. Получим x + y, прибавляя y раз 1 к числу x. Начальной конфигурацией алгоритма служит x, y, 0, 0, 0, .... Типичной конфигурацией в процессе вычисления является
Определим алгоритм следующим образом:
Заданный алгоритм вычисляет функцию x + y. Пример 3.3. Докажите МНР-вычислимость функции Решение. Составим алгоритм для начальной конфигурации x, 0, 0, ... . Типичной конфигурацией в процессе вычисления является:
Следующий алгоритм МНР - вычисляет функцию.
Вопросы для контроля: 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|



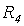




 в регистрах R1, R2, R3,…. перед началом вычислений, называется начальной конфигурацией.
в регистрах R1, R2, R3,…. перед началом вычислений, называется начальной конфигурацией. )
)
 )
)
 ). Функция f называется вычислимой на МНР (или МНР-вычислимой), если существует такой алгоритм P, что:
). Функция f называется вычислимой на МНР (или МНР-вычислимой), если существует такой алгоритм P, что: