
|
|
Анализ, упрощение и синтез переключательных схем.
Составим для этой формулы таблицу истинности. Из таблицы видно, что цепь замкнута в 5 возможных случаях из 10 возможных: когда замкнуты все три контакта, только р1 и р3, только р1, только р2 и р3, толькор2. Произведя равносильные преобразования,
Мы провели анализ данной схемы, который выявил условия, при которых цепь замкнута, и обнаружили возможность ее упрощения, т.е. замены схемой с теми же свойствами, но с меньшим числом контактов. Советский математик О.Б. Лупанов установил, что любую схему, соответствующую формуле с п переменными, всегда можно упростить так, что число контактов в ней не превысит
Решим теперь такую задачу: построить цепь с тремя независимыми контактами, которая проводит ток тогда и только тогда, когда замкнуты ровно два контакта. Формула F(x, y, z), соответствующая искомой схеме, принимает значение 1тогда и только тогда, когда это значение принимают две из трех переменных x, y, z. Напишем СДНФ формулы F: В задаче использован общий метод построения (синтеза) переключательной схемы по заданным ее свойствам.
Вопросы для контроля:
Раздел 7. Логика предикатов. Понятие предиката Понятие ``предикат'' обобщает понятие ``высказывание''. Неформально говоря, предикат – это высказывание, в которое можно подставлять аргументы. Если аргумент один – то предикат выражает свойство аргумента, если больше – то отношение между аргументами. Пример предикатов. Возьмём высказывания: ``Сократ - человек'', ``Платон - человек''. Оба эти высказывания выражают свойство ``быть человеком''. Таким образом, мы можем рассматривать предикат ``быть человеком'' и говорить, что он выполняется для Сократа и Платона. Возьмём высказывание: ``расстояние от Иркутска до Москвы 5 тысяч километров''. Вместо него мы можем записать предикат ``расстояние'' (означающий, что первый и второй аргумент этого предиката находятся на расстоянии, равном третьему аргументу) для аргументов ``Иркутск'', ``Москва'' и ``5 тысяч километров''. Пример рассуждения, не выразимого в логике высказываний. Все люди смертны. Сократ - человек. Следовательно, Сократ смертен. Это рассуждение на языке логики высказываний можно записать тремя отдельными высказываниями. Однако никакой связи между ними установить не удастся. На языке логики предикатов эти предложения можно выразить с помощью двух предикатов: ``быть человеком'' и ``быть смертным''. Первое предложение устанавливает связь между этими предикатами. 7.2. Способа задания предиката 1) Высказывательной формой, т. е. следует задать высказывательную форму и множество объектов для переменных 2) Табличный
Табличный способ применяется тогда, когда мало переменных (от 1 до 3), от которых зависит предикат и множество объектов, на котором задан данный предикат невелико. N-местная высказывательная форма - высказывательная форма, зависящая от N переменных. Если поменять порядок следования переменных в предикате, то это будет другой предикат. Если порядок следования не задан, то берётся по алфавиту, а потом по индексам (возрастание). Если при каком-то значении переменной высказывательная форма, не имеющая знаков логических операций, теряет смысл, то её принято считать ложной. Упорядоченная n-ка - совокупность n не обязательно различных объектов вместе с заданным порядком их расположения. {а; п; е; л; ь; с; и; н} = {с; п; а; н; и; е; л; ь} - для множества (а; п; е; л; ь; с; и; н) ≠ (с; п; а; н; и; е; л; ь) - для упорядоченной n-ки Декартово произведение (произведение n множеств) - такое множество упорядоченных n-ок, в которых на 1-ом месте объект из 1-ого множества, на 2-ом из 2-ого: Пусть Mx = {a; b; c}, My = {1; 2}, тогда их декартово произведение равно: Mx * My = {(a; 1); (b; 2); (a; 2); (c; 1); (c; 2); (b; 1)} 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Чтобы изучить свойства переключательной схемы, выявить ее возможности и особенности, достаточно рассмотреть соответствующую этой схеме формулу. Так, например, схеме на рисунке соответствует формула
Чтобы изучить свойства переключательной схемы, выявить ее возможности и особенности, достаточно рассмотреть соответствующую этой схеме формулу. Так, например, схеме на рисунке соответствует формула 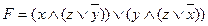 .
.
 ,видим, что один из идентичных переключателей, например, р3, лишний.
,видим, что один из идентичных переключателей, например, р3, лишний. .
.
 . Построим схему, соответствующую этой формуле (рис.).
. Построим схему, соответствующую этой формуле (рис.). (x) = <x - нечетное>, Mx = N
(x) = <x - нечетное>, Mx = N
 (x) =
(x) =  - истина при x < 0
- истина при x < 0 (x) =
(x) = 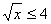 - ложь при x < 0
- ложь при x < 0