
|
|
Равносильные преобразования. Упрощение формулЕсли в равносильные формулы всюду вместо какой-нибудь переменной подставить одну и ту же формулу, то вновь полученные формулы также окажутся равносильными в соответствии с правилом подстановки. Таким способом из каждой равносильности можно получить сколько угодно новых равносильностей. Пример 1:Если в законе де Моргана Если какую-нибудь формулу Тогда для формулы из примера 2 можно провести следующие замены:
По свойству транзитивности отношения равносильности можем утверждать, что Замену одной формулы другой, ей равносильной, называют равносильным преобразованием формулы. Под упрощением формулы, не содержащей знаков импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая не содержит отрицаний неэлементарных формул (в частности, двойных отрицаний) или содержит в совокупности меньшее число знаков конъюнкции и дизъюнкции, чем исходная. Пример 2: Упростим формулу
На первом шаге мы применили закон, преобразующий импликацию в дизъюнкцию. На втором шаге применили коммутативный закон. На третьем шаге применили закон идемпотентности. На четвертом – закон де Моргана. И на пятом – закон двойного отрицания. Замечание 1. Если некоторая формула является тавтологией, то и всякая равносильная ей формула также является тавтологией. Таким образом, равносильные преобразования можно также применять для доказательства тождественной истинности тех или иных формул. Для этого данную формулу нужно равносильными преобразованиями привести к одной из формул, которые являются тавтологиями. Замечание 2. Некоторые тавтологии и равносильности объединены в пары (закон противоречия и закон альтернативы, коммутативный, ассоциативный законы и т.д.). В этих соответствиях проявляется так называемый принцип двойственности. Две формулы, не содержащие знаков импликации и эквиваленции, называются двойственными, если каждую из них можно получить из другой заменой знаков Принцип двойственности утверждает следующее: Теорема 2.2: Если две формулы, не содержащие знаков импликации и эквиваленции, равносильны, то и двойственные им формулы также равносильны. Вопросы для контроля: 1. Равносильные предложения. Равносильные формулы. 2. Свойства отношения равносильности. 3. Равносильные преобразования. 4. Упрощение формул. 5. Применение равносильных преобразований. 6. Принцип двойственности. Раздел 3. Нормальные формы для формул алгебры высказываний Нормальные формы Нормальная форма – это синтаксически однозначный способ записи формулы, реализующей данную функцию. Пользуясь известными законами логики, всякую формулу можно преобразовать в равносильную ей формулу вида Пример 3.1: В больших формулах или при многократных преобразованиях принято знак конъюнкции опускать (по аналогии со знаком умножения): Такая форма называется дизъюнктивной нормальной формой (ДНФ). Отдельный элемент ДНФ называется элементарной конъюнкцией или конституентой единицы. Аналогично любую формулу можно привести к равносильной ей формуле, которая будет являться конъюнкцией элементов, каждый из которых будет представлять собой дизъюнкцию логических переменных со знаком отрицания или без него. То есть, каждую формулу можно привести к равносильной ей формуле вида Пример 3.2: Отдельный элемент КНФ называется элементарной дизъюнкцией или конституентой нуля. Очевидно, что каждая формула имеет бесконечно много ДНФ и КНФ. Пример 3.3: Найдем несколько ДНФ для формулы 1) 2) 3) 4) 5)

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
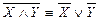 вместо Х подставить
вместо Х подставить 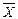 , а вместо Y подставить
, а вместо Y подставить  , то получим новую равносильность
, то получим новую равносильность  . Справедливость полученной равносильности легко проверить с помощью таблицы истинности.
. Справедливость полученной равносильности легко проверить с помощью таблицы истинности. , являющуюся частью формулы F, заменить формулой
, являющуюся частью формулы F, заменить формулой  , равносильной формуле
, равносильной формуле  – закон двойного отрицания;
– закон двойного отрицания;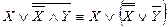 – закон де Моргана;
– закон де Моргана; – закон двойного отрицания;
– закон двойного отрицания; – закон ассоциативности;
– закон ассоциативности; – закон идемпотентности.
– закон идемпотентности. .
. .
. .
. соответственно на
соответственно на  .
. , где
, где  и каждое
и каждое  – либо переменная, либо отрицание переменной, либо конъюнкция переменных или их отрицаний. Другими словами, любую формулу можно привести к равносильной ей формуле простого стандартного вида, которой будет являться дизъюнкция элементов, каждый из которых представляет собой конъюнкцию отдельных различных логических переменных либо со знаком отрицания, либо без него.
– либо переменная, либо отрицание переменной, либо конъюнкция переменных или их отрицаний. Другими словами, любую формулу можно привести к равносильной ей формуле простого стандартного вида, которой будет являться дизъюнкция элементов, каждый из которых представляет собой конъюнкцию отдельных различных логических переменных либо со знаком отрицания, либо без него. . Мы видим, что после проведенных преобразований формула представляет собой дизъюнкцию трех конъюнкций.
. Мы видим, что после проведенных преобразований формула представляет собой дизъюнкцию трех конъюнкций.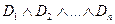 , где
, где  и каждое
и каждое  – либо переменная, либо отрицание переменной, либо дизъюнкция переменных или их отрицаний. Такая форма называется конъюнктивной нормальной формой (КНФ).
– либо переменная, либо отрицание переменной, либо дизъюнкция переменных или их отрицаний. Такая форма называется конъюнктивной нормальной формой (КНФ).
 .
.



