
|
|
Основные правила получения тавтологийРазличают два основных правила образования тавтологий. Правило 1. (правило заключения; правило отделения или правило modus ponens). Если формулы F и Доказательство. Докажем методом «от противного». Предположим, что существует набор значений переменных, при которых значение формулы Н = 0. Тогда, так как F = 1 (по условию формула F – тавтология), значение импликации Правило 2. (правило подстановки). Если формула F, содержащая пропозициональную переменную Х, является тавтологией, то подстановка в формулу F всюду вместо переменной Х любой формулы Н снова приводит к тавтологии. Новая формула при этом обозначается Пример 13:
Вопросы для контроля: 1. Высказывания. Высказывательные формы. Кванторы. 2. Логические связки. Логические операции. 3. Формулы логики высказываний. 4. Таблицы истинности. 5. Классификация формул логики высказываний. 6. Значение тавтологий. 7. Правила получения тавтологий. Раздел 2. Логическая равносильность формул Отношение равносильности С помощью таблиц истинности можно установить, при каких наборах значений истинности входящих переменных формула будет принимать истинное или ложное значение (а также высказывание, имеющее соответствующую логическую структуру), какие формулы будут тавтологиями или противоречиями, а также установить, являются ли две данные формулы равносильными. В логике говорят, что два предложения равносильны, если они одновременно истинны, либо одновременно ложны. Слово «одновременно» в этой фразе неоднозначно. Так, для предложений «Завтра будет вторник» и «Вчера было воскресенье» это слово имеет буквальный смысл: в понедельник они оба истинны, а в остальные дни недели – оба ложны. Для уравнений «х = 2» и «2х = 4» «одновременно» означает «при одних и тех же значениях переменной». Прогнозы «Завтра будет дождь» и «Неверно, что завтра не будет дождя» одновременно подтвердятся (окажутся истинными) либо не подтвердятся (окажутся ложными). В сущности, это один и тот же прогноз, выраженный в двух разных формах, которые можно представить формулами Х и
Видим, что значения истинности в первом и последнем столбцах совпадают. Такие формулы, как и соответствующие им предложения, естественно считать равносильными. Формулы F1 и F2 называются равносильными, если их эквиваленция Равносильность двух формул записывается так: Проверить, равносильны ли формулы, можно двумя способами: 1) составить их эквиваленцию и с помощью таблицы истинности проверить, не является ли она тавтологией; 2) для каждой формулы составить таблицу истинности и сравнить итоговые результаты; если в итоговых столбцах при одинаковых наборах значений переменных значения истинности обеих формул будут равны, то формулы являются равносильными. Пример 1: Выяснить, являются ли формулы равносильными: 1) Решение. 1) Воспользуемся для определения равносильности первым способом, то есть выясним, является ли эквиваленция формул Составим эквиваленцию формул:
Из итогового столбца таблицы истинности видно, что составленная эквиваленция является тавтологией и, значит, 2) Для того чтобы выяснить являются ли формулы В формуле
В формуле
Сравнивая итоговые столбцы составленных таблиц истинности (так как таблицы начинаются одинаково, мы можем не обращать внимание на наборы значений переменных), видим, что они не совпадают и, следовательно, формулы не равносильны ( Выражение Справедлива теорема о свойствах отношения равносильности: Теорема 2.1. Отношение равносильности между формулами алгебры высказываний: 1) рефлексивно: 2) симметрично: если 3) транзитивно: если Законы логики Равносильности формул логики высказываний часто называют законами логики. Перечислим наиболее важные из них: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. Законы логики используются для упрощения сложных формул и для доказательства тождественной истинности или ложности формул. Упрощение формул. Пример 1. Упростить формулу (АvВ) ^(АvС) Аналогично пункту в) вынесем за скобки высказывание А. Пример 2. Упростить выражение v ^ Решение. v ^ v - поглощение Пример 3. Упростить выражение ^ v ^ Всякую формулу можно преобразовать так, что в ней не будет отрицаний сложных высказываний - все отрицания будут применяться только к простым высказываниям. Решение.1. Воспользуемся формулой де Моргана, получим: Любую формулу можно тождественно преобразовать так, что в ней не будут использованы: Пример 5. Преобразовать формулу Пример 6. Преобразовать формулу Эквиваленция выражается через конъюнкцию и импликацию:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
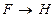 являются тавтологиями, то формула Н также является тавтологией.
являются тавтологиями, то формула Н также является тавтологией.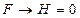 . Получили противоречие с условием (
. Получили противоречие с условием ( 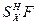 .
.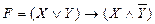 (самостоятельно докажите, что она является тавтологией). Пусть
(самостоятельно докажите, что она является тавтологией). Пусть 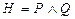 . Тогда
. Тогда 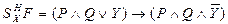 также является тавтологией (самостоятельно убедитесь в этом с помощью таблицы истинности).
также является тавтологией (самостоятельно убедитесь в этом с помощью таблицы истинности).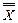 . Эти формулы одновременно принимают значение «истина» либо значение «ложь». Для проверки достаточно составить таблицу истинности:
. Эти формулы одновременно принимают значение «истина» либо значение «ложь». Для проверки достаточно составить таблицу истинности: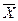
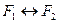 – тавтология.
– тавтология.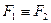 (читается: формула F1 равносильна формуле F2).
(читается: формула F1 равносильна формуле F2).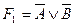 ,
, 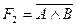 ; 2)
; 2) 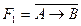 ,
, 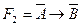 .
.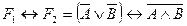 . Полученная формула содержит две различные переменные (А и В) и 6 операций: 1)
. Полученная формула содержит две различные переменные (А и В) и 6 операций: 1) 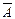 ; 2)
; 2) 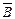 ; 3)
; 3)  ; 4)
; 4) 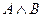 ; 5)
; 5) 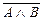 ; 6)
; 6) 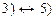 . Значит, в соответствующей таблице истинности будет 5 строк и 8 столбцов:
. Значит, в соответствующей таблице истинности будет 5 строк и 8 столбцов:

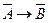
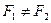 ).
).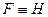 не является формулой (так как символ «
не является формулой (так как символ « 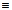 » не относится к какой-либо логической операции). Оно выражает отношение между формулами (также как равенство между числами, параллельность между прямыми и т.п.).
» не относится к какой-либо логической операции). Оно выражает отношение между формулами (также как равенство между числами, параллельность между прямыми и т.п.).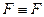 ;
;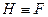 ;
; , то
, то 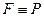 .
.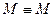 – закон тождества.
– закон тождества. – закон исключенного третьего
– закон исключенного третьего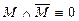 – закон противоречия
– закон противоречия
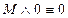
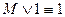
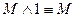
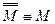 – закон двойного отрицания
– закон двойного отрицания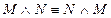 – коммутативность конъюнкции
– коммутативность конъюнкции – коммутативность дизъюнкции
– коммутативность дизъюнкции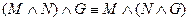 – ассоциативность конъюнкции
– ассоциативность конъюнкции – ассоциативность дизъюнкции
– ассоциативность дизъюнкции – дистрибутивность конъюнкции
– дистрибутивность конъюнкции – дистрибутивность дизъюнкции
– дистрибутивность дизъюнкции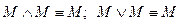 – законы идемпотентности
– законы идемпотентности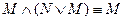 ;
;  – законы поглощения
– законы поглощения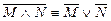 ;
; 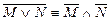 – законы де Моргана
– законы де Моргана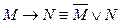 – закон, выражающий импликацию через дизъюнкцию
– закон, выражающий импликацию через дизъюнкцию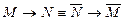 – закон контрапозиции
– закон контрапозиции – законы, выражающие эквиваленцию через другие логические операции
– законы, выражающие эквиваленцию через другие логические операции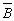
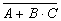 так, чтобы не было отрицаний сложных высказываний. Примечание!!!! знак «+» - дизъюнкция; знак «∙»-конъюнкция.
так, чтобы не было отрицаний сложных высказываний. Примечание!!!! знак «+» - дизъюнкция; знак «∙»-конъюнкция.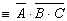
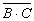 применим еще раз формулу де Моргана, получим:
применим еще раз формулу де Моргана, получим: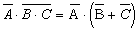
 так, чтобы в ней не использовались знаки логического сложения.
так, чтобы в ней не использовались знаки логического сложения.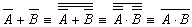
 так, чтобы в ней не использовались знаки логического умножения.
так, чтобы в ней не использовались знаки логического умножения.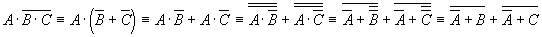
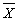
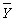
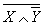
 (5),
(5),