
|
|
Вычислить значение логического выражения (формулы ЛВ) – значит найти значение истинности этого выражения при заданных значениях истинности составляющих переменных.При вычислении значения формулы ЛВ логические операции (если нет скобок) вычисляются в определенном порядке: 1) негация (отрицание); 2) конъюнкция; 3) дизъюнкция; 4) импликация и 5) эквиваленция. Пример 10: Даны формулы. Определить порядок вычисления формул: 1. 1) отрицание 2. 1) отрицание Удобной формой записи при нахождении значений формулы, соответствующих всевозможным наборам значений ее переменных, является таблица, которую называют таблицей истинности. Число наборов значений, которые могут принимать п переменных, находится как 2п. Сформулируем алгоритм построения таблицы истинности сложного высказывания: 1. Вычислить количество строк и столбцов в таблице истинности. Пусть в формуле п различных переменных и k операций. Переменные считаем каждую только один раз, а символы операций – все, сколько есть. Тогда число строк в таблице равно 2п + 1 (число наборов значений переменных плюс строка заголовка), а число столбцов в таблице равно n + k. 2. Начертить таблицу. 3. Заполнить строку заголовка. В строке заголовка записываем промежуточные формулы, начиная с элементарных и учитывая порядок выполнения операций. Вместо промежуточных формул, если они большие, можно записывать их порядковые номера (из порядка выполнения операций). 4. Заполнить оставшиеся строки таблицы, начиная с первого столбца. При вычислении значений промежуточных формул, надо помнить, что в каждой операции участвует не более двух формул (может быть и не элементарных). Пример 11: Составить таблицы истинности для формул: 1) 1. Определим порядок выполнения операций: 1) отрицание Заполняем строку заголовка, начиная с элементарных формул:
Заполняем первый столбик значениями истинности переменной К, для этого число пустых строк делим пополам (4 : 2 = 2) и в половине пишем значение «истина», а в оставшейся половине – «ложь»: Заполняем второй столбик значениями истинности переменной С. Для этого число пустых строк делим на 4 (4 : 4 = 1) и попеременно записываем в строки по одному значению «истина» и «ложь» таким образом, чтобы каждому значению истинности переменной К соответствовали оба значения истинности переменной С:
Начиная с третьего столбика, заполняем строки результатами выполнения операций. В третьем столбике записываем результат выполнения операции отрицания
В четвертом столбике записываем результаты выполнения дизъюнкции В пятом столбике записываем результаты выполнения операции конъюнкции И, наконец, в шестом столбике записываем результаты выполнения итоговой операции импликации
Из итогового результата мы можем сделать следующий вывод: какие бы по смыслу элементарные высказывания не составляли высказывание, соответствующее данной логической структуре, в итоге мы получим истинное высказывание. 2. Определим порядок выполнения операций: 1) отрицание
Заполняем первый столбик значениями истинности переменной А, для этого число пустых строк делим пополам (8 : 2 = 4) и в половине пишем значение «истина», а в оставшейся половине – «ложь»: Заполняем второй столбик значениями истинности переменной В. Для этого число пустых строк делим на 4 (8 : 4 = 2) и попеременно записываем в строки по одному значению «истина» и «ложь» таким образом, чтобы каждому значению истинности переменной А соответствовали по два значения истинности переменной В: Заполняем третий столбик значениями истинности переменной С. Для этого число пустых строк делим на 8 (8 : 8 = 1) и попеременно записываем в строки по одному значению «истина» и «ложь» таким образом, чтобы каждому значению истинности переменной В соответствовали оба значения истинности переменной С:
Заполняем четвертый столбик результатами выполнения операции отрицания Аналогичным образом заполняем пятый столбик результатами операции отрицания
В шестом столбике записываем результаты выполнения операции дизъюнкции И, наконец, в седьмом столбике записываем результат выполнения итоговой операции эквиваленции
Вывод следующий: истинность высказывания, имеющего данную логическую структуру, зависит от значений истинности составляющих его элементарных высказываний. Классификация формул Формулы алгебры высказываний подразделяются на следующие типы: выполнимые, тавтологии, опровержимые и тождественно ложные (противоречия). Подстановка в формулу вместо переменных каких-либо их значений называется конкретизацией формулы. Формула называется выполнимой, если некоторая ее конкретизация является истинным высказыванием. То есть формула Формула называется тождественно истинной или тавтологией, если любая ее конкретизация является истинным высказыванием. Формула называется опровержимой, если некоторая ее конкретизация является ложным высказыванием. Формула называется тождественно ложной или противоречием, если любая ее конкретизация является ложным высказыванием. Для того чтобы определить, к какому типу относится формула, достаточно составить для нее таблицу истинности. Так, первая формула из 11 примера является тавтологией (она при любых наборах значений переменных принимает истинное значение), а вторую формулу можно назвать как выполнимой, так и опровержимой (так как она при разных конкретизациях принимает как истинные, так и ложные значения). Значение тавтологий Основное значение тавтологий состоит в том, что некоторые из них представляют правильные способы умозаключения, то есть такие способы, которые от истинных посылок всегда приводят к истинным выводам. Именно такие рассуждения углубляют наши знания и обогащают их истинными сведениями. Например, любая тавтология вида Пример 12: Схема логического умозаключения, описываемого тавтологией Пусть истинность утверждений 1) и 2) установлена. Одновременный вывод двух взаимоисключающих предложений У и Такой метод доказательства называется методом приведения противоположного утверждения к абсурду. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . Порядок вычисления следующий:
. Порядок вычисления следующий: ; 2) конъюнкция
; 2) конъюнкция  ; 3) дизъюнкция
; 3) дизъюнкция  ; 4) импликация
; 4) импликация  и, наконец, эквиваленция
и, наконец, эквиваленция  .
. . Порядок вычисления следующий:
. Порядок вычисления следующий: ; 3) конъюнкция
; 3) конъюнкция  ; 4) дизъюнкция
; 4) дизъюнкция  ; и 5) эквиваленция
; и 5) эквиваленция  .
. ; 2)
; 2)  .
. ; 2) дизъюнкция
; 2) дизъюнкция 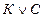 ; 3) конъюнкция
; 3) конъюнкция  и 4) импликация
и 4) импликация  .
. ; 2) отрицание
; 2) отрицание 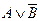 и 4) эквиваленция
и 4) эквиваленция  . Нарисуем таблицу и заполним строку заголовка, начиная с элементарных формул:
. Нарисуем таблицу и заполним строку заголовка, начиная с элементарных формул: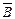 . При этом смотрим, на значения истинности переменной В в соответствующих строках:
. При этом смотрим, на значения истинности переменной В в соответствующих строках: . При этом используем значения истинности переменной А и результаты операции
. При этом используем значения истинности переменной А и результаты операции  . При этом используем результаты предыдущей операции и операции
. При этом используем результаты предыдущей операции и операции  выполнима, если существуют такие конкретные высказывания А, В, …, С, что
выполнима, если существуют такие конкретные высказывания А, В, …, С, что  .
. соответствует некоторой общей схеме логического умозаключения.
соответствует некоторой общей схеме логического умозаключения. , часто используется в математических доказательствах. Она состоит в следующем. Допустим, что требуется доказать истинность некоторого утверждения Х. Предполагаем, что истинно его отрицание
, часто используется в математических доказательствах. Она состоит в следующем. Допустим, что требуется доказать истинность некоторого утверждения Х. Предполагаем, что истинно его отрицание 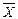 . Затем доказываем, что существует некоторое утверждение У, для которого истинными являются оба утверждения: 1)
. Затем доказываем, что существует некоторое утверждение У, для которого истинными являются оба утверждения: 1)  и 2)
и 2)  . Доказательства истинности этих импликаций зависят от содержания конкретных высказываний Х и У и устанавливаются на основании методов и законов той математической теории, к которой они относятся.
. Доказательства истинности этих импликаций зависят от содержания конкретных высказываний Х и У и устанавливаются на основании методов и законов той математической теории, к которой они относятся. является противоречием. Тогда получаем, что наше предположение об истинности предложения
является противоречием. Тогда получаем, что наше предположение об истинности предложения