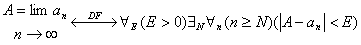|
|
Понятие отношений. Свойства отношений.Бинарные отношения связывают два объекта, бывают: <, >, ║, ≤, ≥, ≠, ┴, =, <быть сверстниками>, родство, дружба, любовь, <жить в одном доме>, равносильность, следование: xRy - объект x находится в отношении R с объектом y. Свойства бинарных отношений: 1) Рефлексивность - xRx (= ,=> , ║, ≤, ≥, ≡, родство, любовь, <друг>) 2) Симметричность - (xRy) 3) Транзитивность - (xRy) 4) Антирефлексивность - 5) Антисимметричность - ((xRy) 6) Связанность - (x≠y) => ((xRy) Вопросы для контроля: 1. Понятие предиката. Способы задания. 2. Понятие множества истинности предиката. 3. Отношения логического следования и логической истинности высказывательных форм 4. Понятие отношений, свойства отношений. Раздел 8. Исчисление предикатов Кванторы общности и существования Кванторы применяются для того, чтобы перейти от высказывательной формы к истинному высказыванию, эта операция называется квантификацией.
Квантификация многоместной высказывательной формы. Квантификация - переход от высказывательной формы к истинному высказыванию. Рассмотрим двуместную высказывательную форму (1) (2) (3) (4) (5) (6) (7) (8) (1) ≡ (2) (3) ≡ (4) Одноименные кванторы можно менять местами (6) => (5) (8) => (7) Если высказывательная форма зависит от n переменных, то при квантификации высказывательной формы по xi переменной, xi переменная становится связанной (связана квантором), при этом все остальные называются свободными. Чтобы перейти от высказывательной формы
Отрицание предложений кванторами. Рассмотрим такой пример: Правила построения отрицания предложения с кванторами: - каждый квантор меняем на противоположный; - отрицание переносим на высказывательную форму. Пример: Предложение: <в каждой стране найдётся город, у всех жителей которого глаза одинакового цвета>. Запись кванторами: Отрицание кванторами: Отрицание предложение: <существует страна, в каждом городе которой найдётся житель с глазами разного цвета>. Численные кванторы а) Не менее n б) Не более n в) Ровно n 1) n = 1 a) б) в) 2) n = 2 а) б) в) Аналогичным образом можно сделать и для n = 3, 4 и так далее.
Символическая запись определений и теорем. Символическая запись используется для того, чтобы люди, находящиеся в разных странах мира и говорящие на разных языках, могли понимать друг друга. Пример: число A называется пределом числовой последовательности Вопросы для контроля: 1. Кванторы общности и существования. 2. Квантификация многоместных высказывательных форм. 3. Отрицание предложений с кванторами. 4. Численные кванторы. 5. Символическая запись определений и теорем. Раздел 9. Алгоритмы. Свойства алгоритмов. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
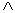 (yRx) (║, =, ┴, ≠, ≤, ≥, дружба, родство, <быть одноклассниками>, <быть тезками>)
(yRx) (║, =, ┴, ≠, ≤, ≥, дружба, родство, <быть одноклассниками>, <быть тезками>)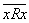 (<, >, ≠, ┴)
(<, >, ≠, ┴) ) (<, >, <жить этажом выше>)
) (<, >, <жить этажом выше>)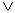 (yRx)) (>, <, ≤, ≥)
(yRx)) (>, <, ≤, ≥)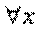 - квантор общности, используется вместо слов: <для любого>, <для каждого>, <для всех>.
- квантор общности, используется вместо слов: <для любого>, <для каждого>, <для всех>. (x2 + y + 1 > 0) - <для всех x верно, что x2 + y + 1 > 0>
(x2 + y + 1 > 0) - <для всех x верно, что x2 + y + 1 > 0> - квантор существования, используется вместо слов: <существует>, <найдется>.
- квантор существования, используется вместо слов: <существует>, <найдется>.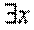 (5 + x =5) - <существует такое x, что 5 + x = 5>
(5 + x =5) - <существует такое x, что 5 + x = 5>
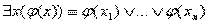
 и всевозможные варианты её квантификации:
и всевозможные варианты её квантификации: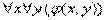





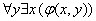
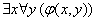
 к истинному высказыванию нужно проквантифицировать её n раз по каждой переменной.
к истинному высказыванию нужно проквантифицировать её n раз по каждой переменной. (отрицание предложения необходимо начинать со слов <неверно, что:>) - <неверно, что все ученики отличники>. Попытаемся перефразировать: <среди учеников есть хотя бы неотличник> или
(отрицание предложения необходимо начинать со слов <неверно, что:>) - <неверно, что все ученики отличники>. Попытаемся перефразировать: <среди учеников есть хотя бы неотличник> или 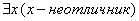 , т. е.
, т. е. 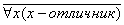 ≡
≡  . Ещё один пример:
. Ещё один пример:  ≡
≡ 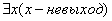 .
.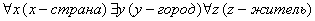 (глаза одинакового цвета)
(глаза одинакового цвета) (неверно, что глаза одинакового цвета)
(неверно, что глаза одинакового цвета) - кубическое уравнение имеет не менее одного корня.
- кубическое уравнение имеет не менее одного корня.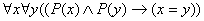 - две прямые пересекаются не более чем в одной точке
- две прямые пересекаются не более чем в одной точке - линейное уравнение имеет один корень
- линейное уравнение имеет один корень - в треугольнике находится не менее двух острых углов
- в треугольнике находится не менее двух острых углов - квадратное уравнение имеет не более двух действительных корней
- квадратное уравнение имеет не более двух действительных корней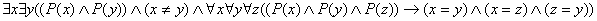 - в прямоугольном треугольнике ровно два острых угла.
- в прямоугольном треугольнике ровно два острых угла.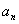 тогда и только тогда, когда для любого E больше <0> существует такое число N, что для любого n, где n больше либо равно N, выполняется условие, что модуль разности числа A и любого числа последовательности меньше E.
тогда и только тогда, когда для любого E больше <0> существует такое число N, что для любого n, где n больше либо равно N, выполняется условие, что модуль разности числа A и любого числа последовательности меньше E.