
|
|
Моделирование нестационарного фильтраВ отличие от описанного выше стационарного фильтра рассмотрим задачу идентификации и моделирования нестационарной системы. Постановка задачи Допустим, что на вход фильтра подается входной сигнал вида r(t) = sin(8sin(4t)*t), time1 = 0:0.005:4; time2 = 4.005:0.005:6; time = [time1 time2]; R = sin(sin(time*4).*time*8); plot(time,R) axis([0 6 –1.1 1.1]); График этого сигнала показан на рис. 9.16.
Нестационарный линейный фильтр описывается следующими рекуррентными
Этот фильтр может быть представлен в системе MATLAB следующим образом: steps1 = length(time1); [Y1,state] = filter([1 –0.5],1,R(1:steps1)); steps2 = length(time2); Y2 = filter([0.9 –0.6],1,R((1:steps2) + steps1),state); Y = [Y1 Y2]; plot(time,Y) График сигнала на выходе этого фильтра показан на рис. 9.17.
Определим такую обучающую последовательность: в качестве целевого выхода T примем массив Y, а входную последовательность P зададим на основе текущего и предшествующего значений входа R. Для использования алгоритмов адаптации представим обучающие последовательности в виде массивов ячеек: T = con2seq(Y); P = con2seq(R); Инициализация сети Сеть создается с помощью функции newlin, которая генерирует веса и смещение lr = 0.5; delays = [0 1]; net = newlin(minmax(cat(2,P{:})),1,delays,lr); [net,a,e] = adapt(net,P,T); Сформированная нейронная сеть имеет следующие весовые коэффициенты и смещение: net.IW{1}, net.b ans = 0.9 –0.6 ans = –3.14e–013 Нетрудно убедиться, что они соответствуют коэффициентам второго фильтра. Проверка сети Построим график погрешности сети (рис. 9.18): plot(time, cat(2,e{:}))
Из анализа этого графика следует, что сети требуется 2.5 с для настройки на реакцию первого фильтра и немногим более 0.2 с для настройки на реакцию второго фильтра. Это объясняется тем, что фактические настройки параметров сети стационарны и соответствуют значениям параметров второго фильтра. Читатель может обратиться к демонстрационному примеру applin4, где исследуется подобная задача. Распознавание образов Часто полезно иметь устройство, которое выполняет распознавание образов. В частности, очень эффективны и выгодны машины, которые могут читать символы. Машина, которая читает банковские чеки, может выполнять за то же самое время намного больше проверок, чем человек. Этот вид приложений сохраняет время и деньги, а также устраняет условия, при которых человек выполняет монотонную, периодически повторяющуюся работу. Демонстрационная программа сценарий appcr1 иллюстрирует, как распознавание символов может быть выполнено в сети с обратным распространением. Постановка задачи Требуется создать нейронную сеть для распознавания 26 символов латинского алфавита. В качестве датчика предполагается использовать систему распознавания, которая выполняет оцифровку каждого символа, находящегося в поле зрения. В результате каждый символ будет представлен шаблоном размера 5´7. Например, символ A может быть представлен, как это показано на рис. 9.19, а и б.
Рис. 9.19 Однако система считывания символов обычно работает неидеально и отдельные элементы символов могут оказаться искаженными (рис. 9.20).
Проектируемая нейронная сеть должна точно распознавать идеальные векторы входа и с максимальной точностью воспроизводить зашумленные векторы. М-функция prprob определяет 26 векторов входа, каждый из которых содержит 35 элементов, этот массив называется алфавитом. М-функция формирует выходные переменные alphabet и targets, которые определяют массивы алфавита и целевых векторов. Массив targets определяется как eye(26). Для того чтобы восстановить шаблон для i-й буквы алфавита, надо выполнить следующие операторы: [alphabet, targets] = prprob; ti = alphabet(:, i); letter{i} = reshape(ti, 5, 7)'; letter{i} Пример: Определим шаблон для символа A, который является первым элементом алфавита: [alphabet, targets] = prprob; i = 2; ti = alphabet(:, i); letter{i} = reshape(ti, 5, 7)'; letter{i} ans = 0 0 1 0 0 0 1 0 1 0 0 1 0 1 0 1 0 0 0 1 1 1 1 1 1 1 0 0 0 1 1 0 0 0 1 Нейронная сеть На вход сети поступает вектор входа с 35 элементами; вектор выхода содержит 26 элементов, только один из которых равен 1, а остальные – 0. Правильно функционирующая сеть должна ответить вектором со значением 1 для элемента, соответствующего номеру символа в алфавите. Кроме того, сеть должна быть способной распознавать символы в условиях действия шума. Предполагается, что шум – это случайная величина со средним значением 0 и стандартным отклонением, меньшим или равным 0.2. Архитектура сети Для работы нейронной сети требуется 35 входов и 26 нейронов в выходном слое. Для решения задачи выберем двухслойную нейронную сеть с логарифмическими сигмоидальными функциями активации в каждом слое. Такая функция активации выбрана потому, что диапазон выходных сигналов для этой функции определен от 0 до 1, и этого достаточно, чтобы сформировать значения выходного вектора. Структурная схема такой нейронной сети показана на рис. 9.21.
Скрытый слой имеет 10 нейронов. Такое число нейронов выбрано на основе опыта Инициализация сети Вызовем М-файл prprob, который формирует массив векторов входа alphabet размера 35´26 с шаблонами символов алфавита и массив целевых векторов targets: [alphabet,targets] = prprob; [R,Q] = size(alphabet); [S2,Q] = size(targets); Двухслойная нейронная сеть создается с помощью команды newff: S1 = 10; net = newff(minmax(alphabet),[S1 S2],{'logsig' 'logsig'},'traingdx'); net.LW{2,1} = net.LW{2,1}*0.01; net.b{2} = net.b{2}*0.01; Структура нейронной сети представлена на рис. 9.22. gensim(net)
Рис. 9.22 Обучение Чтобы создать нейронную сеть, которая может обрабатывать зашумленные векторы входа, следует выполнить обучение сети как на идеальных, так и на зашумленных векторах. Сначала сеть обучается на идеальных векторах, пока не будет обеспечена минимальная сумма квадратов погрешностей. Затем сеть обучается на 10 наборах идеальных и зашумленных векторов. Две копии свободного от шума алфавита используются для того, чтобы сохранить способность сети классифицировать идеальные векторы входа. К сожалению, после того, как описанная выше сеть обучилась классифицировать сильно зашумленные векторы, она потеряла способность правильно классифицировать некоторые 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Рис. 9.16
Рис. 9.16 (9.3)
(9.3) Рис. 9.17
Рис. 9.17 Рис. 9.18
Рис. 9.18 а
а
 Рис. 9.20
Рис. 9.20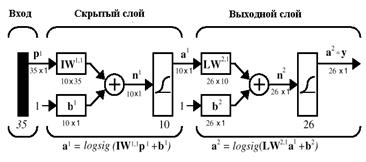 Рис. 9.21
Рис. 9.21


