
|
|
Матрицы весов и векторы смещенийПеречисленные ниже свойства объекта net включают перечень функций, которые
IW массив ячеек Матрицы весов входа. Массив ячеек IW размера Nl´Ni, где Nl – число слоев numLayers и Ni – число входов numInputs сети net, каждый элемент которого является матрицей весов, связывающей слой i со входом j сети; структура этого массива согласована с матрицей связности inputConnect(i, j). Каждая матрица весов должна иметь число строк, равное параметру layers{i}.size, а число столбцов должно удовлетворять соотношению net.inputs{j}.size * length(net.inputWeights{i,j}.delays) и соответствовать параметру inputWeights{i, j}.size. LW массив ячеек Матрицы весов слоя. Массив ячеек LW размера Nl´ Nl, где Nl – число слоев numLayers сети net, каждый элемент которого является матрицей весов, связывающей слой i со слоем j сети; структура этого массива согласована с матрицей связности layerConnect(i, j). net.layers{j}.size * length(net.layerWeights{i,j}.delays) и соответствовать параметру layerWeights{i, j}.size. b массив ячеек Векторы смещений. Вектор ячеек b размера Nl´1, где Nl – число слоев numLayers объекта net, каждый элемент которого является вектором смещений для слоя i сети; структура Информационные поля В структуре объекта net имеются поля, предназначенные для записи информации.
hint массив записей Значения полей объекта network. Это свойство обеспечивает информацию о текущих userdata массив записей Поле для записи информации пользователя. Это свойство обеспечивает место для записи информации, относящейся к нейронной сети. Предусмотрено только одно поле В заключение следует отметить, что для получения полной информации о структуре полей инициированного объекта network следует применять М-функцию fieldnames(<имя_сети>), которая будет отражать текущее состояние нейронной сети. Формирование моделей нейронных сетей Модели сетей
Блок SIMULINK:
Синтаксис: net = network net = network(numInputs, numLayers, biasConnect, inputConnect, Описание: Функция network – это конструктор класса объектов network object, используемых Функция net = network создает шаблон нейронной сети net, значения полей которого обнулены. Функция net = network(numInputs, numLayers, biasConnect, inputConnect, layerConnect, outputConnect, targetConnect) применяется как конструктор класса для написания моделей нейронных сетей. Выходной аргумент net – имя нейронной сети. Пример: Создадим шаблон нейронной сети с двумя входами (numInputs = 2), тремя слоями (numLayers = 3) и следующими матрицами связности: BiasConnect = [1; 0; 0] размера numLayers´1; inputConnect = [1 1; 0 0; 0 0] размера numLayers´numInputs; layerConnect = [0 0 0; 1 0 0; 0 1 0] размера numLayers´numLayers; outputConnect = [0 0 1] размера 1´ numLayers; targetConnect = [0 0 1] размера 1´ numLayers. net = network(2, 3, [1; 0; 0], [1 1; 0 0; 0 0], [0 0 0; 1 0 0; 0 1 0], ... [0 0 1], [0 0 1]); gensim(net) % Рис.11.1 Получим структуру, представленную на рис. 11.1.
Если раскрыть блок Neural Network, то можно выявить структуру сети, обусловленную матрицами связности inputConnect и layerConnect (рис. 11.2).
Из анализа рис. 11.2 следует, что оба входа p{1} и p{2} действуют только на слой 1, Раскроем слои 1, 2 и 3 (рис. 11.3, а–в).
Рис. 11.3 На рис. 11.3, а показана схема слоя 1 со следующими обозначениями: p{1} – описатель входа 1 на слое 1; p{2} – описатель входа 2 на слое 1; Delays 1 – линия задержки для входа 1; Delays 2 – линия задержки для входа 2; IW{1,1} – описатель матрицы весов для входа 1 на слое 1; IW{1,2} – описатель матрицы весов для входа 2 на слое 1; b{1} – описатель вектора смещений на слое 1; netsum – функция накопления для слоя 1; purelin – функция активации для слоя 1; a{1} – описатель выхода на слое 1. На рис. 11.3, б показана схема слоя 2 со следующими обозначениями: a{1} – описатель входа на слое 2; Delays 1 – линия задержки; LW{2,1} – описатель матрицы весов связей слоев 1 и 2; netsum – функция накопления для слоя 2; purelin – функция активации для слоя 2; a{2} – описатель выхода на слое 2. На рис. 11.3, в показана схема слоя 3 со следующими обозначениями: a{2} – описатель входа на слое 3; Delays 1 – линия задержки; LW{3,2} – описатель матрицы весов связей слоев 2 и 3; netsum – функция накопления для слоя 3; purelin – функция активации для слоя 3; a{3} – описатель выхода на слое 3. Введем линии задержки для входов 1 и 2, а также для слоя 3 (рис. 11.4): net.inputWeights{1,1}.delays = [0 1]; net.inputWeights{1,2}.delays = [1 2]; net.layerWeights{3,2}.delays = [0 1 2];
Рис. 11.4 На рис. 11.4 показаны развернутые блоки задержек для всех слоев сети. На схемах выходы этих блоков обозначаются следующим образом: pd{1,1} – входная последовательность [p1(t), p1(t–1)] для входа 1 на слое 1; pd{1,2} – входная последовательность [p2(t–1), p2(t–2)] для входа 2 на слое 1; pd{2,1} – последовательность сигналов, поступающая со слоя 1 на слой 2; pd{3,2} – последовательность сигналов, поступающая со слоя 2 на слой 3. Рассмотрим описатель матрицы весов на примере весов входа для слоя 1 (рис. 11.5).
Эта схема использует следующие обозначения: pd{1,1} – вектор входной последовательности; IW{1,1}(1,:) – строка матрицы весов; dotprod1 – скалярное произведение z = w*p; iz{1,1} – массив взвешенных входов. Установим параметры нейронной сети и векторов входа: net.inputs{1}.range = [0 1]; net.inputs{2}.range = [0 1]; net.b{1}=–1/4; net.IW{1,1} = [ 0.5 0.5 ]; net.IW{1,2} = [ 0.5 0.25]; net.LW{2,1} = [ 0.5 ]; net.LW{3,2} = [ 0.5 0.25 1]; P = [0.5 1; 1 0.5]; После этого модель нейронной сети может быть промоделирована либо используя Построенная модель будет использована при описании методов sim и gensim. Справка: help network/network Сопутствующие функции: GENSIM. Однослойные сети Персептрон
Синтаксис: net = newp(PR,s,tf,lf) Описание: Персептроны предназначены для решения задач классификации входных векторов, относящихся к классу линейно отделимых. Функция net = newp(PR, s, tf, lf) формирует нейронную сеть персептрона. Входные аргументы: PR – массив размера R´2 минимальных и максимальных значений для R векторов входа; s – число нейронов; tf – функция активации из списка {hardlim, hardlims}, по умолчанию hardlim; lf – обучающая функция из списка {learnp, learnpn}, по умолчанию learnp. Выходные аргументы: net – объект класса network object. Свойства: Персептрон – это однослойная нейронная сеть с функциями взвешивания dotprod, накопления потенциала netsum и выбранной функцией активации. Слой характеризуется матрицей весов и вектором смещений, которые инициализируются М-функцией initzero. Адаптация и обучение выполняются М-функциями adaptwb и trainwb, которые модифицируют значения весов и смещений до тех пор, пока не будет достигнуто требуемое значение критерия качества обучения в виде средней абсолютной ошибки, вычисляемой М-функцией mae. Пример: Создать персептрон с одним нейроном, входной вектор которого имеет 2 элемента, значения которых не выходят за пределы диапазона (рис. 11.6): net = newp([0 1; 0 1],1); gensim(net) % Рис.11.6
Определим следующую последовательность двухэлементных векторов входа P, P = {[0; 0] [0; 1] [1; 0] [1; 1]}; Обучим персептрон выполнять операцию ЛОГИЧЕСКОЕ И. С этой целью для полного набора входных векторов сформируем последовательность целей: P1 = cat(2, P{:}); T1 = num2cell(P1(1, :) & P1(2, :)) T1 = [0] [0] [0] [1] Применим процедуру адаптации, установив число проходов равным 10: net.adaptParam.passes = 10; net = adapt(net,P,T1); Вектор весов и смещение можно определить следующим образом: net.IW{1}, net.b{1} ans = 2 1 ans = –3 Таким образом, разделяющая линия имеет вид: L: 2p1 + p2 – 3 = 0. Промоделируем спроектированную нейронную сеть, подав входную обучающую Y = sim(net,P) Y = [0] [0] [0] [1] Настройка параметров сети выполнена правильно. Обучим персептрон выполнять операцию НЕИСКЛЮЧАЮЩЕЕ ИЛИ. С этой целью для полного набора входных векторов Р сформируем последовательность целей: P1 = cat(2, P{:}); T2 = num2cell(P1(1, :) | P1(2, :)) T2 = [0] [1] [1] [1] Применим процедуру обучения, установив число циклов равным 20: net.trainParam.epochs = 20; net = train(net,P,T2); Вектор весов и смещение можно определить следующим образом: net.IW{1}, net.b{1} net.IW{1}, net.b{1} ans = 2 2 ans = –2 Таким образом, разделяющая линия имеет вид: L: 2p1 + 2p2 – 2 = 0. Промоделируем спроектированную нейронную сеть, подав входную обучающую Y = sim(net,P) Y = [0] [1] [1] [1] Обучение и настройка сети выполнены правильно. Замечание: Персептроны решают задачу классификации линейно отделимых входных векторов за конечное время. В случае больших по длине входных векторов функция обучения learnpn может быть по времени выполнения предпочтительнее функции обучения learnp. Сопутствующие функции: SIM, INIT, ADAPT, TRAIN, HARDLIM, HARDLIMS, LEARNP, LEARNPN. Линейные сети
Синтаксис: net = newlin(PR,s,id,lr) net = newlin(PR,s,0,P) Описание: Линейные слои находят применение при решении задач аппроксимации, фильтрации Функция net = newlin(PR, s, id, lr) формирует нейронную сеть в виде линейного слоя. Входные аргументы: PR – массив размера R´2 минимальных и максимальных значений для R векторов входа; s – число нейронов; id – описание линии задержки на входе сети, по умолчанию [0]; lr – параметр скорости настройки, по умолчанию 0.01. Выходные аргументы: net – объект класса network object с архитектурой линейного слоя. Функция net = newlin(PR, s, 0, P), где P – матрица векторов входа, формирует линейный слой с параметром скорости настройки, гарантирующим максимальную степень Пример: Сформировать линейный слой, который для заданного входа воспроизводит заданный отклик системы. Архитектура линейного слоя: линия задержки типа [0 1 2], 1 нейрон, вектор входа net = newlin([–1 1], 1, [0 1 2], 0.01); gensim(net) % Рис.11.7 Элементы линейного слоя показаны на рис. 11.7. Характерная особенность этого слоя – наличие линии задержки, что свидетельствует о том, что такая нейронная сеть является динамической.
Сформируем следующие обучающие последовательности векторов входа и цели: P1 = {0 –1 1 1 0 –1 1 0 0 1}; T1 = {0 –1 0 2 1 –1 0 1 0 1}; P2 = {1 0 –1 –1 1 1 1 0 –1}; T2 = {2 1 –1 –2 0 2 2 1 0}; Выполним обучение, используя только обучающие последовательности P1 и T1: net = train(net,P1,T1); Характеристика процедуры обучения показана на рис. 11.8. Из ее анализа следует, что требуемая точность обучения достигается на 73-м цикле. Соответствующие значения весов и смещения следующие: net.IW{1}, net.b{1} ans = 0.8751 0.8875 –0.1336 ans = 0.0619
Выполним моделирование сети для всех значений входа, объединяющих векторы Р1 и Р2: Y1 = sim(net,[P1 P2]); Результаты моделирования показаны на рис. 11.10 в виде зависимости Y1; последовательность целей, объединяющая векторы T1 и T2, соответствует зависимости Т3. Теперь выполним обучение сети на всем объеме обучающих данных, соответствующем объединению векторов входа {[P1 P2]} и векторов целей {[T1 T2]}: net = init(net); P3 = [P1 P2]; T3 = [T1 T2]; net.trainParam.epochs = 200; net.trainParam.goal = 0.01; net = train(net,P3,T3);
В этом случае процедура обучения не достигает предельной точности в течение 200 циклов обучения и, судя по виду кривой, имеет статическую ошибку. Значения весов и смещений несколько изменяются: net.IW{1}, net.b{1} ans = 0.9242 0.9869 0.0339 ans = 0.0602 Соответствующая дискретная модель динамического линейного слоя имеет вид: yk = 0.9242rk + 0.9869rk –1 + 0.0339rk –2 + 0.0602. Результаты моделирования показаны на рис. 11.10 в виде зависимости Y3. Y3 = sim(net,[P1 P2])
Из сравнения кривых Y3 и Y1 следует, что точность воспроизведения целевой последовательности на интервале тактов времени с 11-й по 19-й стала выше и несколько уменьшилась на 5-м и 9-м тактах. В целом сформированный динамический линейный слой достаточно точно отслеживает кривую цели на последовательностях входов, не участвовавших в обучении. Алгоритм: Линейный слой использует функцию взвешивания dotprod, функцию накопления Адаптация и обучение выполняются М-функциями adaptwb и trainwb, которые модифицируют веса и смещения, используя М-функцию learnwh, до тех пор пока не будет достигнуто требуемое значение критерия качества обучения в виде средней квадратичной ошибки, вычисляемой М-функцией mse. Сопутствующие функции: NEWLIND, SIM, INIT, ADAPT, TRAIN.
Синтаксис: net = newlind(P, T) Описание: Линейный слой LIND использует для расчета весов и смещений процедуру решения систем линейных алгебраических уравнений на основе метода наименьших квадратов, и поэтому в наибольшей степени он приспособлен для решения задач аппроксимации, когда требуется подобрать коэффициенты аппроксимирующей функции. В задачах управления такой линейный слой можно применять для идентификации параметров динамических систем. Функция net = newlind(P, T) формирует нейронную сеть, используя только обучающие последовательности входа P размера R´Q и цели T размера S´Q. Выходом является объект класса network object с архитектурой линейного слоя. Пример: Требуется сформировать линейный слой, который обеспечивает для заданного входа P выход, близкий к цели T, если заданы следующие обучающие последовательности: P = 0:3; T = [0.0 2.0 4.1 5.9]; Анализ данных подсказывает, что требуется найти аппроксимирующую кривую, которая близка к зависимости t = 2p. Применение линейного слоя LIND в данном случае вполне оправдано. net = newlind(P,T); gensim(net) % Рис.11.11
Значения весов и смещений равны: net.IW{1}, net.b{1} ans = 1.9800 ans = 0.3000 Соответствующая аппроксимирующая кривая описывается соотношением yk = 1.9800rk + 0.3000. Выполним моделирование сформированного линейного слоя: Y = sim(net,P) Y = 0.0300 2.0100 3.9900 5.9700 Читатель может самостоятельно убедиться, построив соответствующие графики Алгоритм: Функция newlind вычисляет значения веса W и смещения B для линейного уровня [W b] * [P; ones] = T. Сопутствующие функции: sim, newlin. Многослойные сети
Синтаксис: net = newff(PR,[S1 S2...SNl],{TF1 TF2...TFNl},btf,blf,pf) Описание: Функция newff предназначена для создания многослойных нейронных сетей прямой передачи сигнала с заданными функциями обучения и настройки, которые используют метод обратного распространения ошибки. Функция net = newff(PR, [S1 S2 ... SNl], {TF1 TF2 ... TFNl}, btf, blf, pf) формирует многослойную нейронную сеть. Входные аргументы: PR – массив размера R´2 минимальных и максимальных значений для R векторов входа; Si – количество нейронов в слое i; TFi – функция активации слоя i, по умолчанию tansig; btf – обучающая функция, реализующая метод обратного распространения, по умолчанию trainlm; blf – функция настройки, реализующая метод обратного распространения, по умолчанию learngdm; pf – критерий качества обучения, по умолчанию mse. Выходные аргументы: net – объект класса network object многослойной нейронной сети. Свойства сети: Функциями активации могут быть любые дифференцируемые функции, например tansig, logsig или purelin. Обучающими функциями могут быть любые функции, реализующие метод обратного распространения: trainlm, trainbfg, trainrp, traingd и др. Функция trainlm является обучающей функцией по умолчанию, поскольку обеспечивает максимальное быстродействие, но требует значительных ресурсов памяти. Если ресурсы памяти недостаточны, воспользуйтесь следующими рекомендациями: · установите значение свойства net.trainParam.mem_reduc равным 2 или более, что снизит требования к памяти, но замедлит обучение; · воспользуйтесь обучающей функцией trainbfg, которая работает медленнее, но требует меньшей памяти, чем М-функция trainlm; · перейдите к обучающей функции trainrp, которая работает медленнее, но требует меньшей памяти, чем М-функция trainbfg. Функциями настройки могут быть функции, реализующие метод обратного распространения: learngd, learngdm. Критерием качества обучения может быть любая дифференцируемая функция: mse, msereg. Пример: Создать нейронную сеть, чтобы обеспечить следующее отображение последовательности входа P в последовательность целей T: P = [0 1 2 3 4 5 6 7 8 9 10]; T = [0 1 2 3 4 3 2 1 2 3 4]; Архитектура нейронной сети: двухслойная сеть с прямой передачей сигнала; первый слой – 5 нейронов с функцией активации tansig; второй слой – 1 нейрон с функцией активации purelin; диапазон изменения входа [0 10]. net = newff([0 10],[5 1],{'tansig' 'purelin'}); gensim(net) % Рис.11.12
Рис. 11.12 Выполним моделирование сети и построим графики сигналов выхода и цели (рис. 11.13): Y = sim(net,P); plot(P, T, P, Y, 'o') % Рис.11.13
Обучим сеть в течение 50 циклов: net.trainParam.epochs = 50; net = train(net,P,T); Характеристика точности обучения показана на рис. 11.14; установившаяся среднеквадратичная ошибка составляет приблизительно 0.02.
Выполним моделирование сформированной двухслойной сети, используя обучающую последовательность входа: Y = sim(net,P); plot(P,T,P,Y,'o') % Рис.11.15 Результаты моделирования показаны на рис. 11.15 и свидетельствуют о хорошем отображении входной последовательности в выходную последовательность.
Алгоритм: Многослойная сеть прямой передачи сигнала включает Nl слоев с функциями взвешивания dotprod, накопления netsum и заданными пользователем функциями активации. Первый слой характеризуется матрицей весов входа, другие слои – матрицами весов выхода предшествующего слоя; все слои имеют смещения. Выход последнего слоя является выходом сети. Веса и смещения каждого слоя инициализируются с помощью М-функции initnw. Режим адаптации реализуется М-функцией adaptwb. Для режима обучения выбирается обучающая функция, реализующая метод обратного распространения ошибки. Оценка качества обучения основана на функциях оценки качества, выбираемых Сопутствующие функции: NEWCF, NEWELM, SIM, INIT, ADAPT, TRAIN.
Сеть прямой передачи с запаздыванием Синтаксис: net = newfftd(PR, ID, [S1 S2 ... SNl], {TF1 TF2 ... TFNl}, btf, blf, pf) Описание: Функция newfftd предназначена для создания многослойных нейронных сетей прямой передачи сигнала с линиями задержки и заданными функциями обучения и настройки, использующими метод обратного распространения ошибки. Функция net = newfftd(PR, ID, [S1 S2 ... SNl], {TF1 TF2 ... TFNl}, btf, blf, pf) формирует динамическую многослойную нейронную сеть. Входные аргументы: PR – массив размера R´2 минимальных и максимальных значений для R векторов входа; ID – вектор параметров линии задержки на входе сети; Si – количество нейронов в слое i; TFi – функция активации слоя i, по умолчанию tansig; btf – обучающая функция, реализующая метод обратного распространения, по умолчанию trainlm; blf – функция настройки, реализующая метод обратного распространения, по умолчанию learngdm; pf – критерий качества обучения, по умолчанию mse. Выходные аргументы: net – объект класса network object динамической многослойной нейронной сети. Свойства сети: Функциями активации могут быть любые дифференцируемые функции, например tansig, logsig или purelin. Обучающими функциями могут быть любые функции, реализующие метод обратного распространения: trainlm, trainbfg, trainrp, traingd и др. Функция trainlm является обучающей функцией по умолчанию, поскольку обеспечивает максимальное быстродействие, но требует значительных ресурсов памяти. Если ресурсы памяти недостаточны, воспользуйтесь следующими рекомендациями: · установите значение свойства net.trainParam.mem_reduc равным 2 или более, что снизит требования к памяти, но замедлит обучение; · воспользуйтесь обучающей функцией trainbfg, которая работает медленнее, но требует меньшей памяти, чем М-функция trainlm; · перейдите к обучающей функции trainrp, которая работает медленнее, но требует меньшей памяти, чем М-функция trainbfg. Функциями настройки могут быть функции, реализующие метод обратного распространения: learngd, learngdm. Критерием качества обучения может быть любая дифференцируемая функция: mse, msereg. Пример: Создать нейронную сеть, чтобы обеспечить следующее отображение последовательности входа P в последовательность целей T: P = {1 0 0 1 1 0 1 0 0 0 0 1 1 0 0 1}; T = {1 –1 0 1 0 –1 1 –1 0 0 0 1 0 –1 0 1}; Архитектура нейронной сети: двухслойная сеть с прямой передачей сигнала и линией задержки [0 1]; первый слой – 5 нейронов с функцией активации tansig; второй слой – net = newfftd([0 1],[0 1],[5 1],{'tansig' 'purelin'}); % Рис.11.16
Обучим сеть в течение 50 циклов и промоделируем, используя в качестве теста net.trainParam.epochs = 50; net = train(net,P,T); Y = sim(net,P) Y = [1] [–1] [0] [1] [0] [–1] [1] [–1] [0] [0] [0] [1] Выход сети точно совпадает с целевой последовательностью. Алгоритм: Многослойная динамическая сеть прямой передачи включает Nl слоев с функциями взвешивания dotprod, функциями накопления netsum и заданными пользователем функциями активации. Первый слой характеризуется матрицей весов входа, другие слои – матрицами весов выхода предшествующего слоя; все слои имеют смещения. Выход последнего слоя является выходом сети. Веса и смещения каждого слоя инициализируются с помощью Режим адаптации реализуется М-функцией adaptwb. Для режима обучения выбирается обучающая функция, использующая метод обратного распространения ошибки. Оценка качества обучения основана на функциях оценки качества, выбираемых Сопутствующие функции: NEWCF, NEWELM, SIM, INIT, ADAPT, TRAIN.
Синтаксис: net = newcf(PR,[S1 S2...SNl],{TF1 TF2...TFNl},btf,blf,pf) Описание: Функция newcf предназначена для создания каскадных нейронных сетей прямой передачи сигнала с заданными функциями обучения и настройки, использующими метод обратного распространения ошибки. Функция net = newcf(PR, [S1 S2 ... SNl], {TF1 TF2 ... TFNl}, btf, blf, pf) формирует Входные аргументы: PR – массив размера R´2 минимальных и максимальных значений для R векторов входа; Si – количество нейронов в слое i; TFi – функция активации слоя i, по умолчанию tansig; btf – обучающая функция, реализующая метод обратного распространения, по умолчанию trainlm; blf – функция настройки, реализующая метод обратного распространения, по умолчанию learngdm; pf – критерий качества обучения, по умолчанию mse. Выходные аргументы: net – объект класса network object каскадной нейронной сети с прямой передачей Свойства сети: Функциями активации могут быть любые дифференцируемые функции, например tansig, logsig или purelin. Обучающими функциями могут быть любые функции, реализующие метод обратного распространения: trainlm, trainbfg, trainrp, traingd и др. Функция trainlm является обучающей функцией по умолчанию, поскольку обеспечивает максимальное быстродействие, но требует значительных ресурсов памяти. Если ресурсы памяти недостаточны, воспользуйтесь следующими рекомендациями: · установите значение свойства net.trainParam.mem_reduc равным 2 или более, что снизит требования к памяти, но замедлит обучение; · воспользуйтесь обучающей функцией trainbfg, которая работает медленнее, но требует меньшей памяти, чем М-функция trainlm; · перейдите к обучающей функции trainrp, которая работает медленнее, но требует меньшей памяти, чем М-функция trainbfg. Функциями настройки могут быть функции, реализующие метод обратного распространения: learngd, learngdm Критерием качества обучения может быть любая дифференцируемая функция: mse, msereg. Пример: Создать каскадную нейронную сеть, чтобы обеспечить следующее отображение P = [0 1 2 3 4 5 6 7 8 9 10]; T = [0 1 2 3 4 3 2 1 2 3 4]; Архитектура нейронной сети: каскадная двухслойная сеть с прямой передачей сигнала; первый слой – 5 нейронов с функцией активации tansig; второй слой – 1 нейрон net = newcf([0 10],[5 1],{'tansig' 'purelin'}); gensim(net) % Рис.11.17 Результат представлен на рис. 11.17.
Рис. 11.17 Обучим сеть в течение 50 циклов: net.trainParam.epochs = 50; net = train(net,P,T); Характеристика точности обучения показана на рис. 11.18; установившаяся среднеквадратичная ошибка составляет приблизительно 0.002, что на порядок выше, чем для сети FF ( см. рис. 11.14).
Выполним моделирование каскадной двухслойной сети, используя обучающую Y = sim(net,P); plot(P,T,P,Y,'o') Результат моделирования представлен на рис. 11.19.
Алгоритм: Каскадная сеть прямой передачи использует функции взвешивания dotprod, накопления netsum и заданные пользователем функции активации. Первый каскад характеризуется матрицей весов входа, другие каскады – матрицами весов выхода предшествующего каскада; все каскады имеют смещения. Выход последнего каскада является выходом сети. Веса и смещения инициализируются с помощью Режим адаптации реализуется М-функцией adaptwb. Для режима обучения выбирается обучающая функция, реализующая метод обратного распространения ошибки. Оценка качества обучения основана на функциях оценки качества, выбираемых Сопутствующие функции: NEWFF, NEWELM, SIM, INIT, ADAPT, TRAIN. Радиальные базисные сети
Синтаксис: net = newrb(P,T,goal,spread) Описание: Радиальные базисные сети предназначены для аппроксимации функций. Функция newrb добавляет нейроны к скрытому слою радиальной базисной сети, пока не будет достигнута допустимая средняя квадратичная ошибка обучения. Функция net = newrb(P, T, goal, spread) формирует радиальную базисную сеть и имеет следующие входные и выходные аргументы. Входные аргументы: P – массив размера R´Q из Q входных векторов, R – число элементов вектора входа; T – массив размера S´Q из Q векторов цели; goal – средняя квадратичная ошибка, по умолчанию 0.0; spread – параметр влияния, по умолчанию 1.0. Выходные аргументы: net – объект класса network object радиальной базисной сети. Свойства сети: Параметр влияния spread существенно влияет на качество аппроксимации функции: чем его значение больше, тем более гладкой будет аппроксимация. Слишком большое значение параметра spread приведет к тому, что для получения гладкой аппроксимации быстро изменяющейся функции потребуется большое количество нейронов; слишком малое значение параметра spread потребует большого количества нейронов для аппроксимации гладкой функции. Пример: Создадим радиальную базисную сеть для следующей обучающей последовательности при средней квадратичной ошибке 0.1 (рис. 11.20): P = 0:3; T = [0.0 2.0 4.1 5.9]; net = newrb(P,T,0.1); net.layers{1}.size ans = 3 gensim(net) % Рис.11.20
Сформированная радиальная базисная сеть имеет 3 нейрона с функцией активации radbas. Выполним моделирование сети для нового входа (рис. 11.21): plot(P,T,'*r','MarkerSize',2,'LineWidth',2) hold on V = sim(net,P); % Векторы входа из обучающего множества plot(P,V,'ob','MarkerSize',8, 'LineWidth',2) P1 = 0.5:2.5; Y = sim(net,P1) plot(P1,Y,'+k','MarkerSize',10, 'LineWidth',2) % Рис.11.21
Алгоритм: Функция newrb создает радиальную базисную сеть с двумя слоями. Первый слой включает нейроны с функцией активации radbas и использует функции взвешивания dist Сеть формируется следующим образом. Изначально первый слой не имеет нейронов. Сеть моделируется и определяется вектор входа с самой большой погрешностью, добавляется нейрон с функцией активации radbas и весами, равными вектору входа, затем вычисляются весовые коэффициенты линейного слоя, чтобы не превысить допустимой средней квадратичной погрешности. Сопутствующие функции: SIM, NEWRBE, NEWGRNN, NEWPNN.
Синтаксис: net = newrbe(P,T,spread) Описание: Функция net = newrb(P, T, spread) формирует радиальную базисную сеть с нулевой ошибкой и имеет следующие входные и выходные аргументы. Входные аргументы: P – массив размера R´Q из Q входных векторов, R – число элементов вектора входа; T – массив размера S´Q из Q векторов цели; spread – параметр влияния, по умолчанию 1.0. Выходные аргументы: net – объект класса network object радиальной базисной сети с нулевой ошибкой. Чем больше значение параметра spread, тем более гладкой будет аппроксимация. Слишком большое значение spread может привести к вычислительным проблемам. Пример: Создадим радиальную базисную сеть с нулевой ошибкой для следующей обучающей последовательности: P = 0:3; T = [0.0 2.0 4.1 5.9]; net = newrbe(P,T); net.layers{1}.size ans = 4 Сформированная радиальная базисная сеть с нулевой ошибкой имеет 4 нейрона в первом слое. Сравните с предыдущим случаем, когда число нейронов было равно трем. Выполним моделирование сети для нового входа (рис. 11.22): plot(P,T,'*r','MarkerSize',2,'LineWidth',2) hold on V = sim(net,P); % Векторы входа из обучающего множества plot(P,V,'ob','MarkerSize',8, 'LineWidth',2) P1 = 0.5:2.5; Y = sim(net,P1) plot(P1,Y,'+k','MarkerSize',10, 'LineWidth',2) % Рис.11.22
Алгоритм: Функция newrbe создает радиальную базисную сеть с двумя слоями. Первый слой включает нейроны с функцией активации radbas и использует функции взвешивания dist Функция newrbe устанавливает веса первого слоя равными P', а смещения – равными 0.8326/spread, в результате радиальная базисная функция пересекает значение 0.5 при значениях взвешенных входов ±spread. Веса второго слоя IW{2,1} и смещения b{2} определяются путем моделирования выходов первого слоя A{1} и последующего решения системы линейных уравнений: [W{2,1} b{2}] * [A{1}; ones] = T Сопутствующие функции: SIM, NEWRB, NEWGRNN, NEWPNN.
Синтаксис: net = newgrnn(P,T,spread) Описание: Обобщенные регрессионные сети являются разновидностью радиальных базисных сетей и используются для анализа временных рядов, решения задач обобщенной регрессии и аппроксимации функций. Характерной особенностью этих сетей является высокая скорость их обучения. Функция net = newgrnn(P, T, spread) формирует обобщенную регрессионную сеть Входные аргументы: P – массив размера R´Q из Q входных векторов, R – число элементов вектора входа; T – массив размера S´Q из Q векторов цели; spread – параметр влияния, по умолчанию 1.0. Выходные аргументы: net – объект класса network object обобщенной регрессионной сети. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
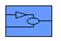
 Рис. 11.1
Рис. 11.1 Рис. 11.2
Рис. 11.2 а
а
 б
б
 в
в


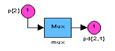

 Рис. 11.5
Рис. 11.5 Рис. 11.6
Рис. 11.6
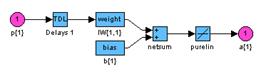
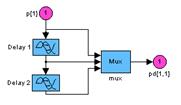 Рис. 11.7
Рис. 11.7
 Рис. 11.8
Рис. 11.8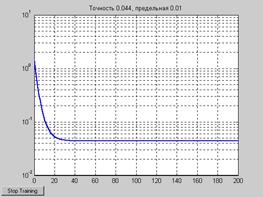 Рис. 11.9
Рис. 11.9 Рис. 11.10
Рис. 11.10
 Рис. 11.11
Рис. 11.11

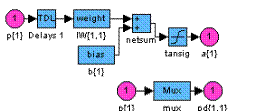

 Рис. 11.13
Рис. 11.13 Рис. 11.14
Рис. 11.14 Рис. 11.15
Рис. 11.15

 Рис. 11.16
Рис. 11.16

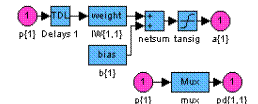

 Рис. 11.18
Рис. 11.18 Рис. 11.19
Рис. 11.19 Рис. 11.20
Рис. 11.20 Рис. 11.21
Рис. 11.21 Рис. 11.22
Рис. 11.22