
|
|
Функции для расчета расстоянийВ ППП NNT используется 4 функции для расчета расстояний между узлами сетки. Функция dist вычисляет евклидово расстояние между нейронами, размещенными
где posi, posj – векторы положения нейронов с номерами i и j. Обратимся к прямоугольной сетке из шести нейронов (см. рис. 7.6) и вычислим соответствующий массив расстояний: pos = gridtop(2,3); d = dist(pos) d = 0 1 1 1.4142 2 2.2361 1 0 1.4142 1 2.2361 2 1 1.4142 0 1 1 1.4142 1.4142 1 1 0 1.4142 1 2 2.2361 1 1.4142 0 1 2.2361 2 1.4142 1 1 0 Этот массив размера 6´6 описывает расстояния между нейронами и содержит на диагонали нули, поскольку они определяют расстояние нейрона до самого себя, а затем, двигаясь вдоль строки, – до второго, третьего и т. д. На рис. 7.9 показано расположение нейронов в узлах прямоугольной сетки. Введем понятие окрестности для прямоугольной сетки. В этом случае окрестность размера 1, или просто окрестность 1, включает базовый нейрон и его непосредственных соседей; окрестность 2 включает нейроны из окрестности 1 и их соседей.
Размер, а соответственно и номер окрестности, определяется максимальным значением координаты смещения нейрона от базового. Вводимое таким способом расстояние
где posi, posj – векторы положения нейронов с номерами i и j. Для вычисления этого расстояния в ППП NNT предназначениа М-функция boxdist. Для конфигурации нейронов, показанной на рис. 7.6, эти расстояния равны: pos = gridtop(2,3); d = boxdist(pos) d = 0 1 1 1 2 2 1 0 1 1 2 2 1 1 0 1 1 1 1 1 1 0 1 1 2 2 1 1 0 1 2 2 1 1 1 0 Расстояние максимального координатного смещения между базовым нейроном 1 и нейронами 2, 3 и 4 равно 1, поскольку они находятся в окрестности 1, а расстояние между базовым нейроном и нейронами 5 и 6 равно 2, и они находятся в окрестности 2. Расстояние максимального координатного смещения от нейронов 3 и 4 до всех других нейронов равно 1. Определим другое расстояние между нейронами, которое учитывает то количество связей, которое необходимо установить, чтобы задать путь движения от базового нейрона. Если задано S нейронов, положение которых определяется векторами pi, i = 1, …, S,
Если евклидово расстояние между нейронами меньше или равно 1, то расстояние связи принимается равным 1; если между нейронами с номерами i и j имеется единственный промежуточный нейрон с номером k, то расстояние связи равно 2, и т. д. Для вычисления расстояния связи в ППП NNT предназначена функции linkdist. pos = gridtop(2,3); d = linkdist(pos) d = 0 1 1 2 2 3 1 0 2 1 3 2 1 2 0 1 1 2 2 1 1 0 2 1 2 3 1 2 0 1 3 2 2 1 1 0 Расстояние связи между базовым нейроном 1 и нейронами 2, 3 равно 1, между базовым нейроном и нейронами 4 и 5 равно 2, между базовым нейроном и нейроном 6 равно 3. Наконец, определим расстояние максимального координатного смещения по формуле
где posi, posj – векторы расположения нейронов с номерами i и j. Для вычисления расстояния максимального координатного смещения в ППП NNT предназначена функции mandist. Вновь обратимся к конфигурации нейронов на рис. 7.6: pos = gridtop(2,3); d = mandist(pos) d = 0 1 1 2 2 3 1 0 2 1 3 2 1 2 0 1 1 2 2 1 1 0 2 1 2 3 1 2 0 1 3 2 2 1 1 0 В случае прямоугольной сетки оно совпадает с расстоянием связи. Архитектура сети Архитектура самоорганизующейся карты Кохонена показана на рис. 7.10.
Эта архитектура аналогична структуре слоя Кохонена за исключением того, что здесь Однако в сети Кохонена выполняется перераспределение нейронов, соседствующих Создание сети Для создания самоорганизующейся карты Кохонена в составе ППП NNT предусмотрена М-функция newsom. Допустим, что требуется создать сеть для обработки двухэлементных векторов входа с диапазоном изменения элементов от 0 до 2 и от 0 до 1 соответственно. Предполагается использовать гексагональную сетку размера 2´3. Тогда для формирования такой нейронной сети достаточно воспользоваться оператором net = newsom([0 2; 0 1], [2 3]); net.layers{1} ans = dimensions: [2 3] distanceFcn: 'linkdist' distances: [6´6 double] initFcn: 'initwb' netInputFcn: 'netsum' positions: [2´6 double] size: 6 topologyFcn: 'hextop' transferFcn: 'compet' userdata: [1´1 struct] Из анализа характеристик этой сети следует, что она использует по умолчанию гексагональную топологию hextop и функцию расстояния linkdist. Для обучения сети зададим следующие 12 двухэлементных векторов входа: P = [0.1 0.3 1.2 1.1 1.8 1.7 0.1 0.3 1.2 1.1 1.8 1.7; ... 0.2 0.1 0.3 0.1 0.3 0.2 1.8 1.8 1.9 1.9 1.7 1.8]; Построим на топографической карте начальное расположение нейронов карты Кохонена и вершины векторов входа (рис. 7.11): plotsom(net.iw{1,1},net.layers{1}.distances) hold on plot(P(1,:),P(2,:),'*k','markersize',10)
Векторы входа помечены символом * и расположены по периметру рисунка, Обучение сети Обучение самоорганизующейся карты Кохонена реализуется повекторно независимо от того, выполняется обучение сети с помощью функции trainwb1 или адаптация с помощью функции adaptwb. В любом случае функция learnsom выполняет настройку элементов весовых векторов нейронов. Прежде всего определяется нейрон-победитель и корректируются его вектор весов
где lr – параметр скорости обучения; А2 – массив параметров соседства для нейронов, расположенных в окрестности нейрона-победителя i, который вычисляется по соотношению
где a(i, q) – элемент выхода нейронной сети; D(i, j) – расстояние между нейронами i и j; nd – размер окрестности нейрона-победителя. В соответствии с соотношениями (6.14) и (6.15) весовые векторы нейрона-победителя и соседних нейронов изменяются в зависимости от значения параметра соседства. Веса нейрона-победителя изменяются пропорционально параметру скорости обучения, а веса соседних нейронов – пропорционально половинному значению этого параметра. Процесс обучения карты Кохонена включает 2 этапа: этап упорядочения векторов весовых коэффициентов в пространстве признаков и этап подстройки. При этом используются следующие параметры обучения сети:
В процессе построения карты Кохонена изменяются 2 параметра: размер окрестности и параметр скорости обучения. Этап упорядочения. На этом этапе используется фиксированное количество шагов.
где max(d) – максимальное расстояние между нейронами; s – номер текущего шага. Параметр скорости обучения изменяется по правилу
Таким образом, он уменьшается от значения order_lr до значения tune_lr. Этап подстройки.Этот этап продолжается в течение оставшейся части процедуры обучения. Размер окрестности на этом этапе остается постоянным и равным
Параметр скорости обучения изменяется по следующему правилу:
Параметр скорости обучения продолжает уменьшаться, но очень медленно, и именно поэтому этот этап именуется подстройкой. Малое значение окрестности и медленное уменьшение параметра скорости обучения хорошо настраивают сеть при сохранении размещения, найденного на предыдущем этапе. Число шагов на этапе подстройки должно значительно превышать число шагов на этапе размещения. На этом этапе происходит тонкая настройка весов нейронов по отношению к набору векторов входа. Как и в случае слоя Кохонена, нейроны карты Кохонена будут упорядочиваться так, чтобы при равномерной плотности векторов входа нейроны карты Кохонена также были распределены равномерно. Если векторы входа распределены неравномерно, то и нейроны на карте Кохонена будут иметь тенденцию распределяться в соответствии с плотностью размещения векторов входа. Таким образом, при обучении карты Кохонена решается не только задача кластеризации входных векторов, но и выполняется частичная классификация. Выполним обучение карты Кохонена размера 2´3 с гексагональной сеткой и с мерой, определяемой расстоянием связи net = newsom([0 2; 0 1], [2 3]); Для обучения сети зададим 12 двухэлементных векторов входа P = [0.1 0.3 1.2 1.1 1.8 1.7 0.1 0.3 1.2 1.1 1.8 1.7; ... 0.2 0.1 0.3 0.1 0.3 0.2 1.8 1.8 1.9 1.9 1.7 1.8]; Зададим количество циклов обучения равным 2000: net.trainParam.epochs = 2000; net.trainParam.show = 100; net = train(net,P); plot(P(1,:),P(2,:),'*','markersize',10) hold on plotsom(net.iw{1,1},net.layers{1}.distances) Результат обучения представлен на рис. 7.12.
Положение нейронов и их нумерация определяются массивом весовых векторов, net.IW{1} ans = 1.2163 0.20902 0.73242 0.46577 1.0645 0.99109 0.4551 1.3893 1.5359 1.8079 1.0888 1.8433 Если промоделировать карту Кохонена на массиве обучающих векторов входа, то будет получен следующий выход сети: a = sim(net,P) a = (2,1) 1 (2,2) 1 (1,3) 1 (1,4) 1 (1,5) 1 (1,6) 1 (4,7) 1 (4,8) 1 (6,9) 1 (6,10) 1 (5,11) 1 (5,12) 1 Это означает, что векторы входов 1 и 2 отнесены к кластеру с номером 2, векторы 3–6 – к кластеру 1, векторы 7–8 – к кластеру 4, векторы 9–10 – к кластеру 6, а векторы 11–12 – Если сформировать произвольный вектор входа, то карта Кохонена должна указать его принадлежность к тому или иному кластеру: a = sim(net,[1.5; 1]) a = (3,1) 1 В данном случае представленный вектор входа отнесен к кластеру с номером 3. Обратите внимание, что векторов такого сорта в обучающей последовательности не было. Рассмотрим еще 2 примера одномерной и двумерной карт Кохонена. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
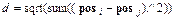 , (7.10)
, (7.10)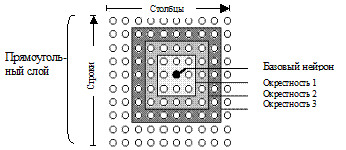 Рис. 7.9
Рис. 7.9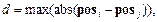 (7.11)
(7.11)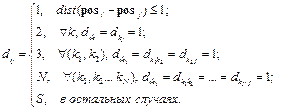 (7.12)
(7.12)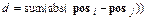 , (7.13)
, (7.13)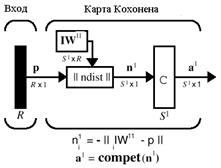 Рис. 7.10
Рис. 7.10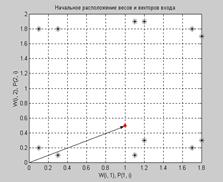 Рис. 7.11
Рис. 7.11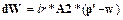 , (7.14)
, (7.14)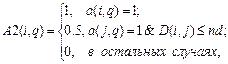 (7.15)
(7.15)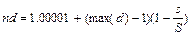 , (7.16)
, (7.16) . (7.17)
. (7.17)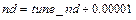 . (7.18)
. (7.18) . (7.19)
. (7.19)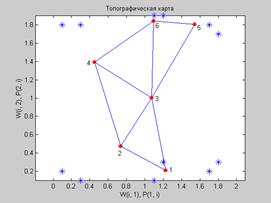 Рис. 7.12
Рис. 7.12