
|
|
Правила настройки параметровПравило LVQ1. LVQ-сеть обучается на основе множества пар вход/выход, составленных из элементов обучающей последовательности {P, T}:
Каждый целевой вектор имеет единственный элемент, равный 1, а остальные равны 0. Для обучения сети необходимо задать вектор входа p, и тогда в конкурирующем слое будет выполнена настройка элементов матрицы весов IW11. Предположим, что весовые коэффициенты нейрона i* наиболее близки к вектору входа p и нейрон i* выигрывает конкуренцию. Тогда конкурирующая функция активации возвращает 1 в качестве элемента i* вектора a1, причем все другие элементы a1 равны 0. Во втором, линейном слое произведение LW21a1 выделяет некоторый столбец матрицы LW21 и связанный с ним класс k*. Таким образом, сеть связывает вектор входа p с классом k*. Это назначение может оказаться либо правильным, либо ошибочным. Поэтому в процессе обучения необходимо откорректировать строку i* матрицы IW11 таким образом, чтобы приблизить ее к вектору p, если назначение правильное, и удалить от вектора p, если назначение неправильное. Основываясь на этих рассуждениях, можно сформулировать правило LVQ1 для настройки параметров сети:
Это правило гарантирует, что при правильной классификации нейрон-победитель приближается к векторам входа, а при неправильной классификации удаляется от них. Правило LVQ2. Это правило предназначено для того, чтобы улучшить настройку параметров сети после применения стандартной процедуры LVQ1. Вариант, реализованный в версии MATLAB 6, известен в литературе [23] как LVQ2.1, и именно он положен в основу алгоритма learnlv2. Правило LVQ2 во многом схоже с правилом LVQ1, за исключением лишь того, что в соответствии с правилом LVQ2 корректируется 2 весовых вектора, ближайших к входному; причем один из них должен быть классифицирован как правильный, а второй – нет. Введем следующие понятия, чтобы дать количественную оценку свойства близости векторов. Пусть величины di и dj обозначают евклидовы расстояния вектора p
то корректировка производится и правило настройки соответствующих весовых векторов выглядит следующим образом:
Процедура обучения Для удобства работы с текстом повторим операторы задания обучающей последовательности и формирования LVQ-сети P = [–3 –2 –2 0 0 0 0 2 2 3; 0 1 –1 2 1 –1 –2 1 –1 0]; Tc = [1 1 1 2 2 2 2 1 1 1]; T = full(ind2vec(Tc)); Выполним синтез LVQ-сети: net = newlvq(minmax(P),4,[.6 .4]); net.inputWeights{1} ans = delays: 0 initFcn: 'midpoint' learn: 1 learnFcn: 'learnlv2' learnParam: [1´1 struct] size: [4 2] userdata: [1´1 struct] weightFcn: 'negdist' Для обучения сети применим М-функцию train, задав количество циклов обучения равным 2000, и значение параметра скорости обучения 0.05: net.trainParam.epochs = 2000; net.trainParam.show = 100; net.trainParam.lr = 0.05; net = train(net,P,T); В результате обучения получим следующие весовые коэффициенты нейронов конкурирующего слоя, которые определяют положения центров кластеризации: V = net.IW{1,1} V = –2.3639 0.0074775 2.3461 0.033489 0 –1.4619 0 1.4731 Построим картину распределения входных векторов по кластерам (рис. 7.19): I1 = find(Tc==1); I2 = find(Tc==2); axis([–4,4,–3,3]), hold on P1 = P(:,I1); P2 = P(:,I2); plot(P1(1,:),P1(2,:),'+k') plot(P2(1,:),P2(2,:),'xb') plot(V(:,1),V(:,2),'or') % Рис.7.19
В свою очередь, массив весов линейного слоя указывает, как центры кластеризации распределяются по классам: net.LW{2} ans = 1 1 0 0 0 0 1 1 Нетрудно видеть, что обучение сети выполнено правильно. Чтобы проверить функционирование сети, подадим на ее вход массив обучающих векторов P: Y = sim(net,P) Yc = vec2ind(Y) Yc = 1 1 1 2 2 2 2 1 1 1 Результат подтверждает, что классификация выполнена правильно. Теперь построим границу, разделяющую области точек, принадлежащих к двум классам. Для этого покроем сеткой прямоугольную область и определим принадлежность каждой точки к тому или иному классу. Текст соответствующего сценария и вспомогательной М-функции приведен ниже
Результат работы этого сценария представлен на рис. 7.20. Здесь же отмечены вычисленные ранее центры кластеризации для синтезированной LVQ-сети. Анализ рисунка подтверждает, что граница между областями не является прямой линией.
Наряду с процедурой обучения можно применить и процедуру адаптации в течение 200 циклов для 10 векторов, что равносильно 2000 циклам обучения с использованием функции train: net.adaptparam.passes = 200; Обучающая последовательность при использовании функции adapt должна быть представлена в виде массивов ячеек: Pseq = con2seq(P); Tseq = con2seq(T); net = adapt(net,Pseq,Tseq); net.IW{1,1} ans = –2.3244 –0.0033588 2.3311 –0.0033019 –0.0003663 1.4704 –0.0003663 –1.4754 Промоделируем сеть, используя массив входных векторов обучающей последовательности: Y = sim(net,P); Yc = vec2ind(Y) Yc = 1 1 1 2 2 2 2 1 1 1 Результаты настройки параметров сети в процессе адаптации практически совпадают с результатами обучения. Единственное, что можно было бы напомнить при этом, что при обучении векторы входа выбираются в случайном порядке и поэтому в некоторых случаях обучение может давать лучшие результаты, чем адаптация. Можно было бы и процедуру адаптации реализовать с использованием случайной последовательности входов, например следующим образом: сформируем 2000 случайных векторов и выполним лишь 1 цикл адаптации: TS = 2000; ind = floor(rand(1,TS)*size(P,2))+1; Pseq = con2seq(P(:,ind)); Tseq = con2seq(T(:,ind)); net.adaptparam.passes = 1; net = adapt(net,Pseq,Tseq); net.IW{1,1} ans = 2.354 –0.061991 –2.362 –0.093345 0 –1.4834 0 1.4539 Y = sim(net,P); Yc = vec2ind(Y) Yc = 1 1 1 2 2 2 2 1 1 1 В результате получаем LVQ-сеть, подобную тем, которые были получены ранее с помощью процедур обучения и адаптации. Читатель может продолжить изучение LVQ-сетей, обратившись к демонстрационной программе demolvq1. Рекуррентные сети В этой главе рассматриваются 2 типа рекуррентных нейронных сетей, представляющих наибольший интерес для пользователей, – это класс сетей Элмана (Elman) и класс сетей Хопфилда (Hopfield). Характерной особенностью архитектуры рекуррентной сети является наличие блоков динамической задержки и обратных связей. Это позволяет таким сетям обрабатывать динамические модели. Обратимся к описанию конкретных типов Сети Элмана Сеть Элмана – это сеть, состоящая из двух слоев, в которой скрытый слой охвачен динамической обратной связью. Это позволяет учесть предысторию наблюдаемых процессов и накопить информацию для выработки правильной стратегии управления. Сети Элмана применяются в системах управления движущимися объектами, при построении систем технического зрения и в других приложениях. В качестве первоисточника следует рекомендовать статью Элмана [10]. По команде help elman можно получить следующую информацию об М-функциях, входящих в состав ППП Neural Network Toolbox и относящихся к построению сетей Элмана:
Архитектура Сеть Элмана – это, как правило, двухслойная сеть с обратной связью от выхода
Рис. 8.1 В качестве функций активации в сети Элмана часто используются: в скрытом, рекуррентном слое – функция гиперболического тангенса tansig, в линейном слое – функция purelin. Такое сочетание функций активации позволяет максимально точно аппроксимировать функции с конечным числом точек разрыва. Единственное требование, предъявляемое к сети, состоит в том, чтобы скрытый слой имел достаточно большое число нейронов, что необходимо для успешной аппроксимации сложных функций. В соответствии со структурной схемой сети Элмана сформируем динамическое описание ее рекуррентного слоя в виде уравнений состояния
Эта рекуррентная матричная форма уравнений состояния лишний раз подчеркивает название изучаемых нейронных сетей. Второй, линейный слой является безынерционным и описывается соотношениями
Ниже сеть Элмана исследуется на примере такой задачи детектирования амплитуды гармонического сигнала. Пусть известно, что на вход нейронной сети поступают выборки из некоторого набора синусоид. Требуется выделить значения амплитуд этих синусоид. Далее рассматриваются выборки из набора двух синусоид с амплитудами 1.0 и 2.0: p1 = sin(1:20); p2 = sin(1:20)*2; Целевыми выходами такой сети являются векторы t1 = ones(1,20); t2 = ones(1,20)*2; Сформируем набор векторов входа и целевых выходов: p = [p1 p2 p1 p2]; t = [t1 t2 t1 t2]; Сформируем обучающую последовательность в виде массивов ячеек: Pseq = con2seq(p); Tseq = con2seq(t); Создание сети В ППП NNT для создания сети Элмана предусмотрена М-функция newelm. Решаемая задача требует, чтобы сеть Элмана на каждом шаге наблюдения значений выборки могла выявить единственный ее параметр – амплитуду синусоиды. Это означает, что сеть должна иметь 1 вход и 1 выход: R = 1; % Число элементов входа S2 = 1;% Число нейронов выходного слоя Рекуррентный слой может иметь любое число нейронов, и чем сложнее задача, тем большее количество нейронов требуется. Остановимся на 10 нейронах рекуррентного слоя: S1 = 10; % Число нейронов рекуррентного слоя Элементы входа для данной задачи изменяются в диапазоне от –2 до 2. Для обучения используется метод градиентного спуска с возмущением и адаптацией параметра скорости настройки, реализованный в виде М-функции traingdx: net = newelm([–2 2],[S1 S2],{'tansig','purelin'},'traingdx'); Сеть использует следующие функции адаптации, инициализации, обучения и оценки качества: adaptFcn: 'adaptwb' initFcn: 'initlay' performFcn: 'mse' trainFcn: 'traingdx' Слои сети Элмана имеют следующие характеристики:
Скрытый слой использует функцию активации tansig, которая для сети Элмана принимается по умолчанию; инициализация весов и смещений реализуется методом NW (Nguen – Widrow) с помощью М-функции initnw. Второй слой использует линейную функцию активации purelin. По умолчанию для настройки весов и смещений используется функция learngdm, Обучение сети Для обучения сети Элмана могут быть использованы как процедура адаптации, так В процессе процедуры адаптации на каждом шаге выполняются следующие действия: · моделирование сети при подаче полного набора векторов входа и вычисление ошибки сети; · вычисление приближенного градиента функционала ошибки относительно весов · настройка весов с использованием функции настройки, выбираемой пользователем; рекомендуется функция learngdm. В процессе процедуры обучения на каждом цикле выполняются следующие действия: · моделирование сети при подаче последовательности входных сигналов, сравнение · вычисление приближенного градиента функционала ошибки относительно весов · настройка весов с использованием функции настройки, выбираемой пользователем; рекомендуется функция traingdx. Сети Элмана не обеспечивают высокой точности решения, поскольку присутствие обратной связи в рекуррентном слое не позволяет вычислить точно градиент функционала. В дальнейшем для обучения сети Элмана используется М-функция train. Ее входными аргументами являются обучающие последовательности Pseq и Tseq, в качестве метода обучения используется метод обратного распространения ошибки с возмущением и адаптацией параметра скорости настройки. Количество циклов обучения принимается равным 1000, периодичность вывода результатов – 20 циклов, конечная погрешность обучения – 0.01: net.trainParam.epochs = 1000; net.trainParam.show = 25; net.trainParam.goal = 0.01; [net,tr] = train(net,Pseq,Tseq); После 500 циклов обучения получим следующий график ошибки (рис. 8.2).
Требуемая точность обучения обеспечивается за 728 циклов. Теперь можно проверить работу сформированной сети. Проверка сети Будем использовать для проверки сети входы обучающей последовательности: figure(2) a = sim(net,Pseq); time = 1:length(p); plot(time, t, '––', time, cat(2,a{:})) axis([1 80 0.8 2.2]) % Рис.8.3 На рис. 8.3 приведены графики входного и выходного сигналов.
Как следует из анализа рисунка, сеть справляется с решением задачи детектирования амплитуды на наборах обучающего множества. Однако неясно, как она будет вести себя на других наборах входа. Обладает ли построенная сеть Элмана свойством обобщения? Попробуем проверить это, выполнив следующие исследования. Подадим на сеть набор сигналов, составленный из двух синусоид с амплитудами 1.6 p3 = sin(1:20)*1.6; t3 = ones(1,20)*1.6; p4 = sin(1:20)*1.2; t4 = ones(1,20)*1.2; pg = [p3 p4 p3 p4]; tg = [t3 t4 t3 t4]; pgseq = con2seq(pg); figure(3) a = sim(net,pgseq); ime = 1:length(pg); plot(time, tg, '––', time, cat(2,a{:})) axis([1 80 0.8 2.2]) Результат представлен на рис. 8.4.
На этот раз сеть хуже справляется с задачей. Сеть стремится детектировать значение амплитуды, но делает это не очень точно. Улучшенное обобщение могло быть получено, обучая сеть на большее количество амплитуд, чем только на значения 1.0 и 2.0. Использование трех или четырех гармонических сигналов с различными амплитудами может привести к намного лучшему датчику амплитуд. Читатель может продолжить изучение сетей Элмана, используя программу appelm1. Сделав копию этой программы, можно продолжить эксперименты, увеличивая количество нейронов в рекуррентном слое или длительность, а также количество входных наборов. Сети Хопфилда Всякий целевой вектор можно рассматривать как набор характерных признаков некоторого объекта. Если создать рекуррентную сеть, положение равновесия которой совпадало бы с этим целевым вектором, то такую сеть можно было бы рассматривать как ассоциативную память. Поступление на вход такой сети некоторого набора признаков в виде начальных условий приводило бы ее в то или иное положение равновесия, что позволяло бы ассоциировать вход с некоторым объектом. Именно такими ассоциативными возможностями и обладают сети Хопфилда. Они относятся к классу рекуррентных нейронных сетей, обладающих тем свойством, что за конечное число тактов времени они из произвольного начального состояния приходят в состояние устойчивого равновесия, называемое аттрактором. Количество таких аттракторов определяет объем ассоциативной памяти сети Хопфилда. Описание сетей Хопфилда читатель может найти в книге [18]. Спроектировать сеть Хопфилда – это значит создать рекуррентную сеть со множеством точек равновесия, таких, что при задании начальных условий сеть в конечном счете приходит в состояние покоя в одной из этих точек. Свойство рекурсии проявляется в том, что выход сети подается обратно на вход. Можно надеяться, что выход сети установится в одной из точек равновесия. Предлагаемый ниже метод синтеза сети Хопфилда не является абсолютно совершенным в том смысле, что синтезируемая сеть в дополнение к желаемым может иметь паразитные точки равновесия. Однако число таких паразитных точек должно быть сведено к минимуму за счет конструирования метода синтеза. Более того, область притяжения точек равновесия должна быть максимально большой. Метод синтеза сети Хопфилда основан на построении системы линейных дифференциальных уравнений первого порядка, которая задана в некотором замкнутом гиперкубе пространства состояний и имеет решения в вершинах этого гиперкуба. Такая сеть Основополагающей работой, связанной с анализом и синтезом модифицированных сетей Хопфилда, является статья [25]. По команде help hopfield можно получить следующую информацию об М-функциях, входящих в состав ППП Neural Network Toolbox и относящихся к построению модифицированных сетей Хопфилда:
Архитектура сети Архитектура модифицированной сети Хопфилда представлена на рис. 8.5.
Вход p устанавливает значения начальных условий. В сети используется линейная функция активации с насыщением satlins, которая описывается следующим образом:
Эта сеть может быть промоделирована с одним или большим количеством векторов входа, которые задаются как начальные условия. После того как начальные условия заданы, сеть генерирует выход, который по обратной связи подается на вход. Этот процесс повторяется много раз, пока выход не установится в положение равновесия. Можно надеяться, что каждый вектор выхода в конечном счете сойдется к одной из точек равновесия, наиболее близкой к входному сигналу. Рассмотрим следующий пример. Предположим, что требуется разработать сеть с двумя устойчивыми точками в вершинах трехмерного куба: T = [–1 –1 1; 1 –1 1]' T = –1 1 –1 –1 1 1 Выполним синтез сети: net = newhop(T); gensim(net) Структура сети представлена на рис. 8.6.
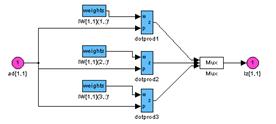
Рис. 8.6 Читателю следует обратить внимание, что на схеме рис. 8.6, а вход и выход слоя совпадают; на рис. 8.6, б показаны используемые в рекуррентном слое элементы. Обратимся к информации о структуре слоя: net.layers{1} ans = dimensions: 3 distanceFcn: 'dist' distances: [3´3 double] initFcn: 'initwb' netInputFcn: 'netsum' positions: [0 1 2] size: 3 topologyFcn: 'hextop' transferFcn: 'satlins' userdata: [1´1 struct] Из этого списка следует, что в слое используется функция инициализации initwb, функция суммирования входов netsum и функция активации satlins. На рис. 8.6, в показан блок, описывающий матрицу весов, которая определяет переходную матрицу динамической модели рекуррентного слоя. Динамическая модель рекуррентного слоя модифицированной сети Хопфилда описывается следующим образом:
При внимательном анализе приведенного соотношения можно действительно убедиться, что матрица весов LW11 равносильна переходной матрице динамической системы, а вектор смещений b1 – вектору передачи единичного входа. Необходимо сформировать эти элементы, если заданы точки равновесия системы t в вершинах гиперкуба. Синтез сети Метод проектирования модифицированных сетей Хопфилда описан в работе [25], Если задано множество целевых точек равновесия, представленных матрицей T, то функция newhop возвращает матрицу весов и вектор смещений для рекуррентного слоя сети Хопфилда. При этом гарантируется, что точки устойчивого равновесия будут соответствовать целевым векторам, но могут появиться и так называемые паразитные точки. Пусть задано Q целевых векторов, образующих матрицу T размера S´Q:
Образуем новую матрицу Y размера S´Q–1 следующего вида:
Вычислим разложение матрицы Y по сингулярным числам:
Далее образуем матрицы
где K – ранг матрицы Y. Построим динамическую систему
где Tt – матрица вида ТР – tТМ; t – динамический параметр (в алгоритме принят равным 10);E – единичная матрица. Вычислим дискретную модель для системы (8.9):
где Ф – переходная матрица вида Соответствующая матрица весов рекуррентного слоя и вектор смещения вычисляются следующим образом:
Когда сеть спроектирована, она может быть проверена с одним или большим числом векторов входа. Весьма вероятно, что векторы входа, близкие к целевым точкам, равновесия найдут свои цели. Способность модифицированной сети Хопфилда быстро обрабатывать наборы векторов входа позволяет проверить сеть за относительно короткое время. Сначала можно проверить, что точки равновесия целевых векторов действительно принадлежат вершинам гиперкуба, а затем можно определить области притяжения этих точек и обнаружить паразитные точки равновесия, если они имеются. Рассмотрим следующий пример. Предположим, что требуется создать модифицированную сеть Хопфилда с двумя точками равновесия, заданными в трехмерном пространстве: T = [–1 –1 1; 1 –1 1]' T = –1 1 –1 –1 1 1 Выполним синтез сети, используя М-функцию newhop: net = newhop(T); Удостоверимся, что разработанная сеть имеет устойчивые состояния в этих двух точках. Выполним моделирование сети Хопфилда, приняв во внимание, что эта сеть не имеет входов Ai = T; [Y,Pf,Af] = sim(net,2,[],Ai); Y Y = –1 1 –1 –1 1 1 Действительно, устойчивые положения равновесия сети находятся в назначенных точках. Зададим другое начальное условие в виде массива ячеек: Ai = {[–0.9; –0.8; 0.7]}; Ai{1,1} ans = –0.9000 –0.8000 0.7000 Эта точка расположена вблизи первого положения равновесия, так что можно ожидать, что сеть будет сходиться именно к этой точке. При таком способе вызова функции sim в качестве второго параметра указываются такт дискретности и количество шагов моделирования: [Y,Pf,Af] = sim(net,{1 5},{},Ai); Y{1} Y = –1 –1 Действительно, из заданного начального состояния сеть вернулась в устойчивое положение равновесия. Желательно, чтобы сеть вела себя аналогичным образом при задании любой начальной точки в пределах куба, вершины которого составлены изо всех комбинаций чисел 1 и –1 в трехмерном пространстве. К сожалению, этого нельзя гарантировать, и достаточно часто сети Хопфилда включают нежелательные паразитные точки равновесия. Пример: Рассмотрим сеть Хопфилда с четырьмя нейронами и определим 4 точки равновесия T = [1 –1; –1 1; 1 1; –1 –1]' T = 1 –1 1 –1 –1 1 1 –1 На рис. 8.7 показаны эти 4 точки равновесия на плоскости состояний сети Хопфилда. plot(T(1,:), T(2,:),'*r') % Рис.8.7 axis([–1.1 1.1 –1.1 1.1]) title('Точки равновесия сети Хопфилда') xlabel('a(1)'), ylabel('a(2)')
Рассчитаем веса и смещения модифицированной сети Хопфилда, использую М-функцию newhop: net = newhop(T); W= net.LW{1,1} b = net.b{1,1} W = 1.1618 0 0 1.1618 b = 3.5934e–017 3.5934e–017 Проверим, принадлежат ли вершины квадрата к сети Хопфилда: Ai = T; [Y,Pf,Af] = sim(net,4,[],Ai) Y = 1 –1 1 –1 –1 1 1 –1 Pf = [] Af = 1 –1 1 –1 –1 1 1 –1 Как и следовало ожидать, выходы сети равны целевым векторам. Теперь проверим поведение сети при случайных начальных условиях: plot(T(1,:), T(2,:),'*r'), hold on axis([–1.1 1.1 –1.1 1.1]) xlabel('a(1)'), ylabel('a(2)') new = newhop(T); [Y,Pf,Af] = sim(net,4,[],T); for i =1:25 a = {rands(2,1)}; [Y,Pf,Af] = sim(net,{1,20},{},a); record = [cell2mat(a) cell2mat(Y)]; start = cell2mat(a); plot(start(1,1), start(2,1), 'kx', record(1,:), record(2,:)) end Результат представлен на рис. 8.8.
Читатель может продолжить изучение модифицированных сетей Хопфилда, обратившись к демонстрационным примерам. Пример двумерной сети можно найти в демонстрации demohop1, пример неустойчивой точки равновесия – в демонстрации demohop2. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . (7.20)
. (7.20)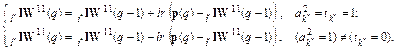 (7.21)
(7.21) (7.22)
(7.22) (7.23)
(7.23) Рис. 7.19
Рис. 7.19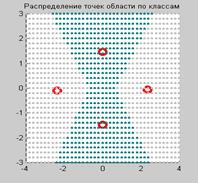 Рис. 7.20
Рис. 7.20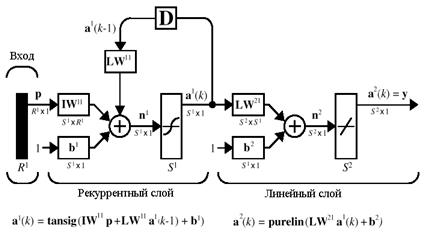
 (8.1)
(8.1) (8.2)
(8.2)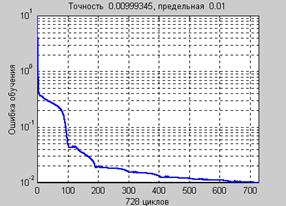 Рис. 8.2
Рис. 8.2 Рис. 8.3
Рис. 8.3 Рис. 8.4
Рис. 8.4 Рис. 8.5
Рис. 8.5 (8.3)
(8.3) a
a
 б
б
 в
в
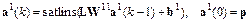 . (8.4)
. (8.4)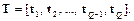 (8.5)
(8.5)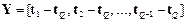 (8.6)
(8.6) (8.7)
(8.7) (8.8)
(8.8)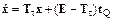 , (8.9)
, (8.9) , (8.10)
, (8.10) ; F – матрица передачи входа вида
; F – матрица передачи входа вида 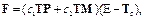 с1 = eh –1, c2 = (1–e–th)/t; h – такт дискретности (в алгоритме принят равным 0.15 c).
с1 = eh –1, c2 = (1–e–th)/t; h – такт дискретности (в алгоритме принят равным 0.15 c). (8.11)
(8.11) Рис. 8.7
Рис. 8.7 Рис. 8.8
Рис. 8.8