
|
|
Градиентные алгоритмы обучения
Синтаксис: [net,TR,Ac,El] = traingd(NET,Pd,Tl,Ai,Q,TS,VV) info = traingd(code) Описание: Функция traingd обучает нейронную сеть, используя алгоритм градиентного спуска GD. Функция при своей работе использует следующие параметры: info = traingd('pdefaults')' info =
Применение функции: Функция обучения traingd используется при создании сетей с помощью методов newff, newcf, newelm, а также при формировании сетей с атрибутами, определяемыми пользователем. Для того чтобы подготовить сеть к обучению, необходимо: · установить свойство сети net.trainFcn равным 'traingd'. Это автоматически установит значения параметров обучения, соответствующие значениям свойства net.trainParam по умолчанию. Для того чтобы фактически обучить сеть, необходимо: · инициализировать нейронную сеть; · присвоить, если это необходимо, требуемые значения параметрам обучения; · применить функцию train. Алгоритм: Функция traingd выполняет процедуру обучения, если функции взвешивания, накопления и активации имеют производные. Для вычисления производных критерия качества обучения (perf) по переменным веса и смещения используется метод обратного распространения ошибки. В соответствии с методом градиентного спуска вектор настраиваемых переменных получает следующие приращения: dX = lr * dperf/dX. Процедура обучения прекращается, когда выполнено одно из следующих условий: · значение функции качества стало меньше предельного; · градиент критерия качества стал меньше значения min_grad; · достигнуто предельное число циклов обучения; · превышено максимальное время, отпущенное на обучение; · ошибка контрольного подмножества превысила ошибку обучающего более чем Пример: Заданы следующие обучающие последовательности входов P и целей T: P = [0 1 2 3 4 5]; T = [0 0 0 1 1 1]; Поскольку соответствие между входом и целью носит явно выраженный нелинейный характер, то будем использовать нейронную сеть с нелинейными сигмоидальными функциями активации. Выберем двухслойную нейронную сеть с прямой передачей сигнала; Формирование сети: net = newff([0 5],[2 1],{'tansig','logsig'},'traingd'); Обучение сети: net.trainParam.epochs = 500; net.trainParam.goal = 0.01; [net,TR] = train(net,P,T); % Рис.11.44 На рис. 11.44 показано, как изменяется точность в процессе обучения; требуемое значение обеспечивается на 332-м цикле обучения.
Выполним моделирование сети: Y = sim(net,P) Y = 0.0669 0.0962 0.1284 0.8350 0.9640 0.9657 Требуемое соответствие между входом и выходом нейронной сети обеспечивается Сопутствующие функции: NEWFF, NEWCF, TRAINGDM, TRAINGDA, TRAINGDX, TRAINLM.
Синтаксис: [net,TR,Ac,El] = traingda(NET,Pd,Tl,Ai,Q,TS,VV) info = traingda(code) Описание: Функция traingda обучает нейронную сеть, используя алгоритм градиентного спуска Функция при своей работе использует следующие параметры: info = traingda('pdefaults')' info =
Применение функции: Функция обучения traingda используется при создании сетей с помощью методов newff, newcf, newelm, а также при формировании сетей с атрибутами, определяемыми пользователем. Для того чтобы подготовить сеть к обучению, необходимо: · установить свойство сети net.trainFcn равным 'traingda'. Это автоматически установит значения параметров обучения, соответствующие значениям свойства net.trainParam по умолчанию. Для того чтобы фактически обучить сеть, необходимо: · инициализировать нейронную сеть; · присвоить, если это необходимо, требуемые значения параметрам обучения; · применить функцию train. Алгоритм: Функция traingda выполняет процедуру обучения, если функции взвешивания, накопления и активации имеют производные. Для вычисления производных критерия качества обучения по переменным веса и смещения используется метод обратного распространения ошибки. В соответствии с методом градиентного спуска вектор настраиваемых переменных получает следующие приращения: dX = lr * dperf/dX. Однако в данном случае, в отличие от алгоритма градиентного спуска, параметр скорости настройки выполняет адаптивную функцию. Он увеличивается в lr_inc раз, если критерий качества обучения сети уменьшается, и это реализуется на каждом цикле обучения. С другой стороны, если критерий качества увеличился более чем в max_perf_inc раз, то начинается коррекция параметра скорости настройки в сторону уменьшения с коэффициентом lr_dec. Процедура обучения прекращается, когда выполнено одно из следующих условий: · значение функции качества стало меньше предельного; · градиент критерия качества стал меньше значения min_grad; · достигнуто предельное число циклов обучения; · превышено максимальное время, отпущенное на обучение; · ошибка контрольного подмножества превысила ошибку обучающего более чем Пример: Заданы следующие обучающие последовательности входов P и целей T: P = [0 1 2 3 4 5]; T = [0 0 0 1 1 1]; Поскольку соответствие между входом и целью носит явно выраженный нелинейный характер, то будем использовать нейронную сеть с нелинейными сигмоидальными функциями активации. Выберем двухслойную нейронную сеть с прямой передачей сигнала; Формирование сети: net = newff([0 5],[2 1],{'tansig','logsig'},'traingda'); Обучение сети: net.trainParam.epochs = 500; net.trainParam.goal = 0.01; [net,TR] = train(net,P,T); % Рис.11.45 TR = epoch: [1´94 double] perf: [1´94 double] vperf: [1´94 double] tperf: [1´94 double] lr: [1´94 double]
На рис. 11.45 показано, как изменяется точность в процессе обучения; требуемое значение обеспечивается на 93-м цикле обучения; при этом параметр скорости настройки постоянно растет и достигает значения приблизительно 0.93 (рис. 11.46).
Выполним моделирование сети: Y = sim(net,P) Y = 0.0376 0.1069 0.1922 0.9121 0.9774 0.9783 Требуемое соответствие между входом и выходом нейронной сети обеспечивается Сопутствующие функции: NEWFF, NEWCF, TRAINGD, TRAINGDM, TRAINGDX, TRAINLM.
Синтаксис: [net,TR,Ac,El] = traingdm(NET,Pd,Tl,Ai,Q,TS,VV) info = traingdm(code) Описание: Функция traingdm обучает нейронную сеть, используя алгоритм градиентного спуска с возмущением GDM. Функция при своей работе использует следующие параметры: info = traingdm('pdefaults')' info =
Применение функции: Функция обучения traingdm используется при создании сетей с помощью методов newff, newcf, newelm, а также при формировании сетей с атрибутами, определяемыми пользователем. Для того чтобы подготовить сеть к обучению, необходимо: · установить свойство сети net.trainFcn равным 'traingdm'. Это автоматически установит значения параметров обучения, соответствующие значениям свойства net.trainParam по умолчанию. Для того чтобы фактически обучить сеть, необходимо: · инициализировать нейронную сеть; · присвоить, если это необходимо, требуемые значения параметрам обучения; · применить функцию train. Алгоритм: Функция traingdm выполняет процедуру обучения, если функции взвешивания, накопления и активации имеют производные. Для вычисления производных критерия качества обучения по переменным веса и смещения используется метод обратного распространения ошибки. В соответствии с методом градиентного спуска с возмущением вектор настраиваемых переменных получает следующие приращения: dX = mc*dXprev + lr*mc*dperf/dX, где dXprev – вектор возмущения весов и смещений с коэффициентом mc. Процедура обучения прекращается, когда выполнено одно из следующих условий: · значение функции качества стало меньше предельного; · градиент критерия качества стал меньше значения min_grad; · достигнуто предельное число циклов обучения; · превышено максимальное время, отпущенное на обучение; · ошибка контрольного подмножества превысила ошибку обучающего более чем Пример: Заданы следующие обучающие последовательности входов P и целей T: P = [0 1 2 3 4 5]; T = [0 0 0 1 1 1]; Поскольку соответствие между входом и целью носит явно выраженный нелинейный характер, то будем использовать нейронную сеть с нелинейными сигмоидальными функциями активации. Выберем двухслойную нейронную сеть с прямой передачей сигнала; Формирование сети: net = newff([0 5],[2 1],{'tansig','logsig'},'traingdm'); Обучение сети: net.trainParam.epochs = 500; net.trainParam.goal = 0.01; net.trainParam.lr = 0.1; [net,TR] = train(net,P,T); % Рис.11.47
На рис. 11.47 показано, как изменяется точность в процессе обучения; требуемое Выполним моделирование сети: Y = sim(net,P) Y = 0.0787 0.0393 0.1006 0.8696 0.8883 0.8884 Требуемое соответствие между входом и выходом нейронной сети обеспечивается Сопутствующие функции: NEWFF, NEWCF, TRAINGD, TRAINGDA, TRAINGDX, TRAINLM.
Синтаксис: [net,TR,Ac,El] = traingdx(NET,Pd,Tl,Ai,Q,TS,VV) info = traingdx(code) Описание: Функция traingdx обучает нейронную сеть, используя алгоритм градиентного спуска Функция при своей работе использует следующие параметры: info = traingdx('pdefaults')' info =
Применение функции: Функция обучения traingdx используется при создании сетей с помощью методов newff, newcf, newelm, а также при формировании сетей с атрибутами, определяемыми пользователем. Для того чтобы подготовить сеть к обучению, необходимо: · установить свойство сети net.trainFcn равным 'traingdx'. Это автоматически установит значения параметров обучения, соответствующие значениям свойства net.trainParam по умолчанию. Для того чтобы фактически обучить сеть, необходимо: · инициализировать нейронную сеть; · присвоить, если это необходимо, требуемые значения параметрам обучения; · применить функцию train. Алгоритм: Функция traingdx выполняет процедуру обучения, если функции взвешивания, накопления и активации имеют производные. Для вычисления производных критерия качества обучения по переменным веса и смещения используется метод обратного распространения ошибки. В соответствии с методом градиентного спуска с возмущением вектор dX = mc*dXprev + lr*mc*dperf/dX, где dXprev – вектор возмущения весов и смещений с коэффициентом mc. Однако в данном случае, в отличие от алгоритма traingdm, параметр скорости настройки выполняет адаптивную функцию. Он увеличивается в lr_inc раз, если критерий качества обучения сети уменьшается, и это реализуется на каждом цикле обучения. Обучение прекращается, когда выполнено одно из следующих условий: · значение функции качества стало меньше предельного; · градиент критерия качества стал меньше значения min_grad; · достигнуто предельное число циклов обучения; · превышено максимальное время, отпущенное на обучение; · ошибка контрольного подмножества превысила ошибку обучающего более чем Пример: Заданы следующие обучающие последовательности входов P и целей T: P = [0 1 2 3 4 5]; T = [0 0 0 1 1 1]; Поскольку соответствие между входом и целью носит явно выраженный нелинейный характер, то будем использовать нейронную сеть с нелинейными сигмоидальными функциями активации. Выберем двухслойную нейронную сеть с прямой передачей сигнала; Формирование сети: net = newff([0 5],[2 1],{'tansig','logsig'},'traingdx'); Обучение сети: net.trainParam.epochs = 500; net.trainParam.goal = 0.01; [net,TR] = train(net,P,T); % Рис.11.48 TR = epoch: [1´106 double] perf: [1´106 double] vperf: [1´106 double] tperf: [1´106 double] lr: [1´106 double]
На рис. 11.48 показано, как изменяется точность в процессе обучения; требуемое значение обеспечивается на 105-м цикле обучения; при этом параметр скорости настройки постоянно растет и достигает значения приблизительно 1.7 (рис. 11.49).
Выполним моделирование сети: Y = sim(net,P) Y = 0.0787 0.0393 0.1006 0.8696 0.8883 0.8884 Требуемое соответствие между входом и выходом нейронной сети обеспечивается Сопутствующие функции: NEWFF, NEWCF, TRAINGD, TRAINGDM, TRAINGDA, TRAINLM.
Синтаксис: [net,TR,Ac,El]= trainrp(NETt,Pd,Tl,Ai,Q,TS,VV) info = trainrp(code) Описание: Функция trainrp обучает нейронную сеть, используя пороговый алгоритм обратного распространения ошибки. Функция при своей работе использует следующие параметры: info = trainrp('pdefaults')' info =
Применение функции: Функция обучения trainrp используется при создании сетей с помощью методов newff, newcf, newelm, а также при формировании сетей с атрибутами, определяемыми пользователем. Для того чтобы подготовить сеть к обучению, необходимо: · установить свойство сети net.trainFcn равным 'trainrp'. Это автоматически установит значения параметров обучения, соответствующие значениям свойства net.trainParam по умолчанию. Для того чтобы фактически обучить сеть, необходимо: · инициализировать нейронную сеть; · присвоить, если это необходимо, требуемые значения параметрам обучения; · применить функцию train. Алгоритм: Функция trainrp выполняет процедуру обучения, если функции взвешивания, накопления и активации имеют производные. Для вычисления производных критерия качества обучения по переменным веса и смещения используется метод обратного распространения ошибки. В соответствии с пороговым алгоритмом обратного распространения вектор настраиваемых переменных получает следующие приращения: dX = deltaX.*sign(gX), где вектору deltaX присваиваются начальные значения delta0, а вектор gX – градиент критерия качества. На каждой итерации элементы deltaX изменяются. Если некоторый элемент вектора gX изменяет знак при переходе к следующей итерации, то соответствующий элемент вектора deltaX умножается на коэффициент delta_dec. Если элемент вектора gX сохраняет знак, то соответствующий элемент вектора deltaX умножается на коэффициент delta_inc [36]. Процедура обучения прекращается, когда выполнено одно из следующих условий: · значение функции качества стало меньше предельного; · градиент критерия качества стал меньше значения min_grad; · достигнуто предельное число циклов обучения; · превышено максимальное время, отпущенное на обучение; · ошибка контрольного подмножества превысила ошибку обучающего более чем Пример: Заданы следующие обучающие последовательности входов P и целей T: P = [0 1 2 3 4 5]; T = [0 0 0 1 1 1]; Поскольку соответствие между входом и целью носит явно выраженный нелинейный характер, то будем использовать нейронную сеть с нелинейными сигмоидальными функциями активации. Выберем двухслойную нейронную сеть с прямой передачей сигнала; Формирование сети: net = newff([0 5],[2 1],{'tansig','logsig'},'trainrp'); Обучение сети: net.trainParam.epochs = 50; net.trainParam.show = 10; net.trainParam.goal = 0.01; [net,TR] = train(net,P,T); % Рис.11.50 На рис. 11.50 показано, как изменяется точность в процессе обучения; требуемое
Выполним моделирование сети: Y = sim(net,P) Y = 0.0696 0.0704 0.1339 0.8934 0.9390 0.9399 Требуемое соответствие между входом и выходом нейронной сети обеспечивается Сопутствующие функции: NEWFF, NEWCF, TRAINGDM, TRAINGDA, TRAINGDX, TRAINLM, TRAINCGP, TRAINCGF, TRAINCGB, TRAINSCG, TRAINOSS, TRAINBFG. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Рис. 11.44
Рис. 11.44 Рис. 11.45
Рис. 11.45 Рис. 11.46
Рис. 11.46 Рис. 11.47
Рис. 11.47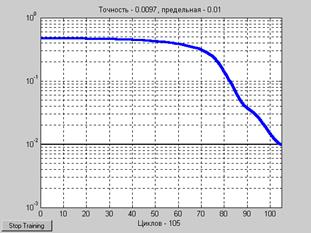 Рис. 11.48
Рис. 11.48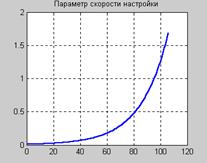 Рис. 11.49
Рис. 11.49 Рис. 11.50
Рис. 11.50