Одномерная карта Кохонена

Рассмотрим 100 двухэлементных входных векторов единичной длины, распределенных равномерно в пределах от 0 до 90°:

angles = 0:0.5*pi/99:0.5*pi;

P = [sin(angles); cos(angles)];

plot(P(1,1:10:end), P(2,1:10:end),'*b'), hold on

График входных векторов приведен на рис. 7.13, а, и на нем символом * отмечено
положение каждого 10-го вектора.

а

б

Рис. 7.13

Сформируем самоорганизующуюся карту Кохонена в виде одномерного слоя из 10 ней­ронов и выполним обучение в течение 2000 циклов:

net = newsom([0 1;0 1], [10]);

net.trainParam.epochs = 2000;

net.trainParam.show = 100;

[net, tr] = train(net,P);

plotsom(net.IW{1,1},net.layers{1}.distances) % Рис.7.13,а

figure(2)

a = sim(net,P);

bar(sum(a')) % Рис.7.13,б

Весовые коэффициенты нейронов, определяющих центры кластеров, отмечены
на рис. 7.13, а цифрами. На рис. 7.13, б показано распределение обучающих векторов
по кластерам. Как и ожидалось, они распределены практически равномерно с разбросом от 8 до 12 векторов в кластере.

Таким образом, сеть подготовлена к кластеризации входных векторов. Определим,
к какому кластеру будет отнесен вектор [1; 0]:

a = sim(net,[1;0])

a = (10,1) 1

Как и следовало ожидать, он отнесен к кластеру с номером 10.

Двумерная карта Кохонена

Этот пример демонстрирует обучение двумерной карты Кохонена. Сначала создадим обучающий набор случайных двумерных векторов, элементы которых распределены
по равномерному закону в интервале [–1 1]:

P = rands(2,1000);

plot(P(1,:),P(2,:),'+') % Рис.7.14

Рис. 7.14

Для кластеризации векторов входа создадим самоорганизующуюся карту Кохонена размера 5´6 с 30 нейронами, размещенными на гексагональной сетке:

net = newsom([–1 1; –1 1],[5,6]);

net.trainParam.epochs = 1000;

net.trainParam.show = 100;

net = train(net,P);

plotsom(net.IW{1,1},net.layers{1}.distances)

Результирующая карта после этапа размещения показана на рис. 7.15, а. Продолжим обучение и зафиксируем карту после 1000 шагов этапа подстройки (рис. 7.15, б), а затем после 4000 шагов (рис. 7.15, в). Нетрудно убедиться, что нейроны карты весьма равномерно покрывают область векторов входа.

а

б

в

Рис. 7.15

Определим принадлежность нового вектора к одному из кластеров карты Кохонена
и построим соответствующую вершину вектора на рис. 7.15, в:

a = sim(net,[0.5;0.3])

a = (19,1) 1

hold on, plot(0.5,0.3,'*k') % Рис.7.15,в

Нетрудно убедиться, что вектор отнесен к 19-му кластеру.

Промоделируем обученную карту Кохонена, используя массив векторов входа:

a = sim(net,P);

bar(sum(a')) % Рис.7.16

Из анализа рис. 7.16 следует, что количество векторов входной последовательности, отнесенных к определенному кластеру, колеблется от 13 до 50.

Рис. 7.16

Таким образом, в процессе обучения двумерная самоорганизующаяся карта Кохонена выполнила кластеризацию массива векторов входа. Следует отметить, что на этапе размещения было выполнено лишь 20 % от общего числа шагов обучения, т. е. 80 % общего времени обучения связано с тонкой подстройкой весовых векторов. Фактически на этом этапе выполняется в определенной степени классификация входных векторов.

Слой нейронов карты Кохонена можно представлять в виде гибкой сетки, которая натянута на пространство входных векторов. В процессе обучения карты, в отличие от обучения слоя Кохонена, участвуют соседи нейрона-победителя, и, таким образом, топологическая карта выглядит более упорядоченной, чем области кластеризации слоя Кохонена.

Читатель может продолжить изучение самоорганизующихся сетей, обратившись
к демонстрационным программам demosm1 и demosm2.

LVQ-сети

Ниже рассматриваются сети для классификации входных векторов, или LVQ (Learning Vector Quantization)-сети. Как правило, они выполняют и кластеризацию и классификацию векторов входа. Эти сети являются развитием самоорганизующихся сетей Кохонена [23].

По команде help lvq можно получить следующую информацию об М-функциях, входящих в состав ППП Neural Network Toolbox и относящихся к построению LVQ-сетей:

Архитектура сети

Архитектура LVQ-сети, предназначенной для классификации входных векторов,
показана на рис. 7.17.

Рис. 7.17

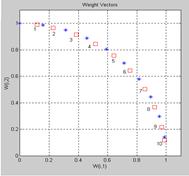
LVQ-cеть имеет 2 слоя: конкурирующий и линейный. Конкурирующий слой выполняет кластеризацию векторов, а линейный слой соотносит кластеры с целевыми классами, заданными пользователем.

Как в конкурирующем, так и в линейном слое приходится 1 нейрон на кластер или целевой класс. Таким образом, конкурирующий слой способен поддержать до S¹ кластеров; эти кластеры, в свою очередь, могут быть соотнесены с S² целевыми классами, причем S² не превышает S¹. Например, предположим, что нейроны 1–3 конкурирующего слоя определяют 3 кластера, которые принадлежат к одному целевому классу #2 линейного слоя. Тогда выходы конкурирующих нейронов 1–3 будут передаваться в линейный слой на нейрон n² с весами, равными 1, а на остальные нейроны с весами, равными 0. Таким образом, нейрон n² возвращает 1, если любой
из трех нейронов 1–3 конкурирующего слоя выигрывает конкуренцию.

Короче говоря, единичный элемент в i-й строке вектора a¹ (остальные элементы a¹ нулевые) однозначно выберет i-й столбец матрицы весов LW²¹ в качестве выхода сети. При этом каждый столбец, в свою очередь, содержит единственный элемент, равный 1, который указывает принадлежность к классу. Таким образом, кластер с номером 1 из слоя 1 может оказаться отнесенным к различным классам в зависимости от значения произведения LW²¹a¹.

Поскольку заранее известно, как кластеры первого слоя соотносятся с целевыми
классами второго слоя, то это позволяет заранее задать элементы матрицы весов LW²¹. Однако чтобы найти правильный кластер для каждого вектора обучающего множества, необходимо выполнить процедуру обучения сети.

Создание сети

В ППП NNT для создания LVQ-сетей предусмотрена М-функция newlvq, обращение
к которой имеет следующий вид:

net = newlvq(PR,S1,PC,LR,LF)

где PR – массив размера R´2 минимальных и максимальных значений для R элементов вектора входа; S1 – количество нейронов конкурирующего слоя; PC – вектор с S² элементами, определяющими процентную долю принадлежности входных векторов к определенному классу; LR – параметр скорости настройки (по умолчанию 0.01); LF – имя функции настройки (по умолчанию для версии MATLAB 5 – 'learnlv2', для версии MATLAB 6 – 'learnlv1').

Предположим, что задано 10 векторов входа и необходимо создать сеть, которая,
во-первых, группирует эти векторы в 4 кластера, а во-вторых, соотносит эти кластеры
с одним из двух выходных классов. Для этого следует использовать LVQ-сеть, первый конкурирующий слой которой имеет 4 нейрона по числу кластеров, а второй линейный слой – 2 нейрона по числу классов.

Зададим обучающую последовательность в следующем виде:

P = [–3 –2 –2 0 0 0 0 2 2 3;

0 1 –1 2 1 –1 –2 1 –1 0];

Tc = [1 1 1 2 2 2 2 1 1 1];

Из структуры обучающей последовательности следует, что 3 первых и 3 последних ее вектора относятся к классу 1, а 4 промежуточных – к классу 2. На рис. 7.18 показано расположение векторов входа.

I1 = find(Tc==1); I2 = find(Tc==2);

axis([–4,4,–3,3]), hold on

plot(P(1,I1),P(2,I1),’+k’)

plot(P(1,I2),P(2,I2),’xb’) % Рис.7.18

Рис. 7.18

Векторы, относящиеся к разным классам, отмечены разными символами. Как следует из расположения векторов, классы не являются линейно отделимыми, и задача не может быть решена с использованием, например, персептрона.

Преобразуем вектор индексов Tc в массив целевых векторов:

T = full(ind2vec(Tc))

T =

1 1 1 0 0 0 0 1 1 1

0 0 0 1 1 1 1 0 0 0

Процентные доли входных векторов в каждом классе равны 0.6 и 0.4 соответственно. Теперь подготовлены все данные, необходимые для вызова функции newlvq. Вызов может быть реализован c использованием следующего оператора

net = newlvq(minmax(P),4,[.6 .4],0.1);

Обучение сети

Не нашли, что искали? Воспользуйтесь поиском по сайту: