
|
|
Примеры радиальных базисных сетейДемонстрационный пример demorb1 иллюстрирует применение радиальной базисной сети для решения задачи аппроксимации функции от одной переменной. Представим функцию f(x) следующим разложением:
где ji(x) – радиальная базисная функция. Тогда идея аппроксимации может быть представлена графически следующим образом. Рассмотрим взвешенную сумму трех радиальных базисных функций, заданных p = –3:.1:3; a1 = radbas(p); a2 = radbas(p–1.5); a3 = radbas(p+2); a = a1 + a2*1 + a3*0.5; plot(p,a1,p,a2,p,a3*0.5,p,a) % Рис. 6.6
Как следует из анализа рис. 6.6 разложение по радиальным базисным функциям обеспечивает необходимую гладкость. Поэтому их применение для аппроксимации произвольных нелинейных зависимостей вполне оправдано. Разложение вида (6.2) может быть реализовано на двухслойной нейронной сети, первый слой которой состоит из радиальных базисных нейронов, а второй – из единственного нейрона с линейной характеристикой, на котором реализуется суммирование выходов нейронов первого слоя. Приступим к формированию радиальной базисной сети. Сформируем обучающее множество и зададим допустимое значение функционала ошибки, равное 0.01, параметр влияния определим равным 1 и будем использовать итерационную процедуру формирования радиальной базисной сети: P = –1:.1:1; T = [–.9602 –.5770 –.0729 .3771 .6405 .6600 .4609 .1336 ... –.2013 –.4344 –.5000 –.3930 –.1647 .0988 .3072 .3960 ... .3449 .1816 –.0312 –.2189 –.3201]; GOAL = 0.01; % Допустимое значение функционала ошибки SPREAD = 1; % Параметр влияния net = newrb(P,T,GOAL,SPREAD); % Создание сети net.layers{1}.size % Число нейронов в скрытом слое ans = 6 Для заданных параметров нейронная сеть состоит из шести нейронов и обеспечивает следующие возможности аппроксимации нелинейных зависимостей после обучения. plot(P,T,'+k') % Точки обучающего множества hold on; X = –1:.01:1; Y = sim(net,X); % Моделирование сети plot(X,Y); % Рис. 6.7 Из анализа рис. 6.7 следует, что при небольшом количестве нейронов скрытого слоя радиальная базисная сеть достаточно хорошо аппроксимирует нелинейную зависимость, заданную обучающим множеством из 21 точки.
В демонстрационных примерах demorb3 и demorb4 исследуется влияние параметра SPREAD на структуру радиальной базисной сети и качество аппроксимации. В демонстрационном примере demorb3 параметр влияния SPREAD установлен равным 0.01. Это означает, что диапазон перекрытия входных значений составляет лишь ±0.01, а поскольку обучающие входы заданы с интервалом 0.1, то входные значения функциями активации не перекрываются. GOAL = 0.01; % Допустимое значение функционала ошибки SPREAD = 0.01; % Параметр влияния net = newrb(P,T,GOAL,SPREAD); % Создание сети net.layers{1}.size % Число нейронов в скрытом слое ans = 19 Это приводит к тому, что, во-первых, увеличивается количество нейронов скрытого слоя с 6 до 19, а во-вторых, не обеспечивается необходимой гладкости аппроксимируемой функции: plot(P,T,'+k') % Точки обучающего множества hold on; X = –1:.01:1; Y = sim(net,X); % Моделирование сети plot(X,Y); % Рис. 6.8
Пример demorb4 иллюстрирует противоположный случай, когда параметр влияния SPREAD выбирается достаточно большим (в данном примере – 12 или больше), то все функции активации перекрываются и каждый базисный нейрон выдает значение, близкое к 1, для всех значений входов. Это приводит к тому, что сеть не реагирует на входные значения. Функция newrb будет пытаться строить сеть, но не сможет обеспечить необходимой точности из-за вычислительных проблем. GOAL = 0.01; % Допустимое значение функционала ошибки SPREAD = 12; % Параметр влияния net = newrb(P,T,GOAL,SPREAD); % Создание сети net.layers{1}.size % Число нейронов в скрытом слое ans = 21 В процессе вычислений возникают трудности с обращением матриц, и об этом выдаются предупреждения; количество нейронов скрытого слоя устанавливается равным 21, plot(P,T,'+k') % Точки обучающего множества hold on; X = –1:.01:1; Y = sim(net,X); % Моделирование сети plot(X,Y); % Рис. 6.9
Вывод из выполненного исследования состоит в том, что параметр влияния SPREAD следует выбирать большим, чем шаг разбиения интервала задания обучающей последовательности, но меньшим размера самого интервала. Для данной задачи это означает, что параметр влияния SPREAD должен быть больше 0.1 и меньше 2. Сети GRNN Нейронные сети GRNN (Generalized Regression Neural Network) описаны в работе [43] и предназначены для решения задач обобщенной регрессии, анализа временных рядов Архитектура сети Архитектура сети GRNN показана на рис. 6.10. Она аналогична архитектуре радиальной базисной сети, но отличается структурой второго слоя, в котором используется блок normprod для вычисления нормированного скалярного произведения строки массива весов LW21 и вектора входа a1 в соответствии со следующим соотношением:
Первый слой – это радиальный базисный слой с числом нейронов, равным числу элементов Q обучающего множества; в качестве начального приближения для матрицы весов выбирается массив P'; смещение b1 устанавливается равным вектор-столбцу с элементами 0.8326/SPREAD. Функция dist вычисляет расстояние между вектором входа и вектором веса нейрона; вход функции активации n1 равен поэлементному произведению взвешенного входа сети на вектор смещения; выход каждого нейрона первого слоя a1 является результатом преобразования вектора n1 радиальной базисной функцией radbas. Если вектор веса нейрона равен транспонированному вектору входа, то взвешенный вход равен 0, а выход функции активации – 1. Если расстояние между вектором входа и вектором веса нейрона равно spread, то выход функции активации будет равен 0.5. Второй слой – это линейный слой с числом нейронов, также равным числу элементов Q обучающего множества, причем в качестве начального приближения для матрицы весов LW{2,1} выбирается массив T. Предположим, что имеем вектор входа pi, близкий к одному из векторов входа pиз обучающего множества. Этот вход pi генерирует значение выхода слоя ai1,близкое к 1. Это приводит к тому, что выход слоя 2 будет близок к ti. Если параметр влияния SPREAD мал, то радиальная базисная функция характеризуется резким спадом и диапазон входных значений, на который реагируют нейроны скрытого слоя, оказывается весьма малым. С увеличением параметра SPREAD наклон радиальной базисной функции становится более гладким, и в этом случае уже несколько нейронов реагируют на значения вектора входа. Тогда на выходе сети формируется вектор, соответствующий среднему нескольких целевых векторов, соответствующих входным векторам обучающего множества, близких к данному вектору входа. Чем больше значение параметра SPREAD, тем большее число нейронов участвует в формировании среднего значения, и в итоге функция, генерируемая сетью, становится более гладкой. Синтез сети Для создания нейронной сети GRNN предназначена М-функция newgrnn. Зададим следующее обучающее множество векторов входа и целей и построим сеть GRNN: P = [4 5 6]; T = [1.5 3.6 6.7]; net = newgrnn(P,T); net.layers{1}.size % Число нейронов в скрытом слое ans = 3 Эта сеть имеет 3 нейрона в скрытом слое. Промоделируем построенную сеть сначала для одного входа, а затем для последовательности входов из интервала [4 7]: p = 4.5; v = sim(net,p); p1 = 4:0.1:7; v1 = sim(net,p1); plot(P,T,'*k',p,v,'ok',p1,v1,'–k','MarkerSize',10,'LineWidth',2) Результат показан на рис. 6.11.
Заметим, что для сети GRNN размер вводимого вектора может отличаться от размера векторов, используемых в обучающей последовательности. Кроме того, в данном случае аппроксимирующая функция может значительно отличаться от значений, соответствующих обучающей последовательности. Демонстрационная программа demogrn1 иллюстрирует, как сети GRNN решают задачи аппроксимации. Определим обучающее множество в виде массивов Р и Т. P = [1 2 3 4 5 6 7 8]; T = [0 1 2 3 2 1 2 1]; Для создания сети GRNN используется функция newgrnn. Примем значение параметра влияния SPREAD немного меньшим, чем шаг задания аргумента функции (в данном случае 1), чтобы построить аппроксимирующую кривую, близкую к заданным точкам. Как мы уже видели ранее, чем меньше значение параметра SPREAD, тем ближе точки аппроксимирующей кривой к заданным, но тем менее гладкой является сама кривая: spread = 0.7; net = newgrnn(P,T,spread); net.layers{1}.size % Число нейронов в скрытом слое ans = 8 A = sim(net,P); plot(P,T,'*k','markersize',10) hold on, plot(P,A,'ok','markersize',10); Результат показан на рис. 6.12.
Моделирование сети для диапазона значений аргумента позволяет увидеть всю P2 = –1:0.1:10; A2 = sim(net,P2); plot(P2,A2,'–k','linewidth',2) hold on, plot(P,T,'*k','markersize',10) Результат показан на рис. 6.13.
Сформированная сеть GRNN использует всего 8 нейронов в скрытом слое и весьма успешно решает задачу аппроксимации и экстраполяции нелинейной зависимости, восстанавливаемой по экспериментальным точкам. Сети PNN Нейронные сети PNN (Probabilistic Neural Networks) описаны в работе [43] и предназначены для решения вероятностных задач, и в частности задач классификации. Архитектура сети Архитектура сети PNN базируется на архитектуре радиальной базисной сети, но в качестве второго слоя использует так называемый конкурирующий слой, который подсчитывает вероятность принадлежности входного вектора к тому или иному классу и в конечном счете сопоставляет вектор с тем классом, вероятность принадлежности к которому выше. Структура сети PNN представлена на рис. 6.14.
Предполагается, что задано обучающее множество, состоящее из Q пар векторов вход/цель. Каждый вектор цели имеет K элементов, указывающих класс принадлежности, и, таким образом, каждый вектор входа ставится в соответствие одному из K классов. Весовая матрица первого слоя IW11 (net.IW{1,1}) формируется с использованием векторов входа из обучающего множества в виде матрицы P'. Когда подается новый вход, блок ||dist|| вычисляет близость нового вектора к векторам обучающего множества; затем вычисленные расстояния умножаются на смещения и подаются на вход функции активации radbas. Вектор обучающего множества, наиболее близкий к вектору входа, будет представлен в векторе выхода a1 числом, близким к 1. Весовая матрица второго слоя LW21 (net.LW{2,1}) соответствует матрице связности T, построенной для данной обучающей последовательности. Эта операция может быть выполнена с помощью М-функции ind2vec, которая преобразует вектор целей в матрицу связности T. Произведение T*a1 определяет элементы вектора a1, соответствующие каждому из K классов. В результате конкурирующая функция активации второго слоя compet формирует на выходе значение, равное 1, для самого большого по величине элемента вектора n2 и 0 в остальных случаях. Таким образом, сеть PNN выполняет классификацию векторов входа по K классам. Синтез сети Для создания нейронной сети PNN предназначена М-функция newpnn. Определим P = [0 0;1 1;0 3;1 4;3 1;4 1;4 3]'; Tc = [1 1 2 2 3 3 3]; Вектор Тс назовем вектором индексов классов. Этому индексному вектору можно T = ind2vec(Tc) T = (1,1) 1 (1,2) 1 (2,3) 1 (2,4) 1 (3,5) 1 (3,6) 1 (3,7) 1 которая определяет принадлежность первых двух векторов к классу 1, двух последующих – к классу 2 и трех последних – к классу 3. Полная матрица Т имеет вид: Т = full(T) Т = 1 1 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 1 1 1 Массивы Р и Т задают обучающее множество, что позволяет выполнить формирование сети, промоделировать ее, используя массив входов P, и удостовериться, что сеть правильно решает задачу классификации на элементах обучающего множества. В результате моделирования сети формируется матрица связности, соответствующая массиву net = newpnn(P,T); net.layers{1}.size % Число нейронов в сети PNN ans = 7 Y = sim(net,P); Yc = vec2ind(Y) Yc = 1 1 2 2 3 3 3 Результат подтверждает правильность решения задачи классификации. Выполним классификацию некоторого набора произвольных векторов р, не принадлежащих обучающему множеству, используя ранее созданную сеть PNN: p = [1 3; 0 1; 5 2]'; Выполняя моделирование сети для этого набора векторов, получаем a = sim(net,p); ac = vec2ind(a) ac = 2 1 3 Фрагмент демонстрационной программы demopnn1 позволяет проиллюстрировать clf reset, drawnow p1 = 0:.05:5; p2 = p1; [P1,P2]=meshgrid(p1,p2); pp = [P1(:) P2(:)]; aa = sim(net,pp'); aa = full(aa); m = mesh(P1,P2,reshape(aa(1,:),length(p1),length(p2))); set(m,'facecolor',[0.75 0.75 0.75],'linestyle','none'); hold on view(3) m = mesh(P1,P2,reshape(aa(2,:),length(p1),length(p2))); set(m,'facecolor',[0 1 0.5],'linestyle','none');, m = mesh(P1,P2,reshape(aa(3,:),length(p1),length(p2))); set(m,'facecolor',[0 1 1],'linestyle','none'); plot3(P(1,:),P(2,:),ones(size(P,2))+0.1,'.','markersize',30) plot3(p(1,:),p(2,:),1.1*ones(size(p,2)),'*','markersize',20,... 'color',[1 0 0]) hold off view(2) Результаты классификации представлены на рис. 6.15 и показывают, что 3 представленных сети вектора, отмеченные звездочками, классифицируются сетью PNN, состоящей из семи нейронов, абсолютно правильно.
В заключение отметим, что сети PNN могут весьма эффективно применяться для решения задач классификации. Если задано достаточно большое обучающее множество, то решения, генерируемые сетями, сходятся к решениям, соответствующим правилу Байеса. Недостаток сетей GRNN и PNN заключается в том, что работают они относительно медленно, поскольку выполняют очень большие объемы вычислений по сравнению с другими типами нейронных сетей. 7. Сети кластеризации В процессе анализа больших информационных массивов данных неизменно возникают задачи, связанные с исследованием топологической структуры данных, их объединением 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , (6.2)
, (6.2) Рис. 6.6
Рис. 6.6 Рис. 6.7
Рис. 6.7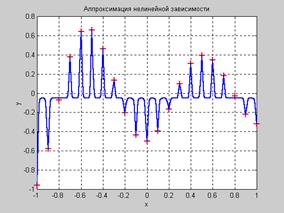 Рис. 6.8
Рис. 6.8 Рис. 6.9
Рис. 6.9 . (6.3)
. (6.3) Рис. 6.10
Рис. 6.10 Рис. 6.11
Рис. 6.11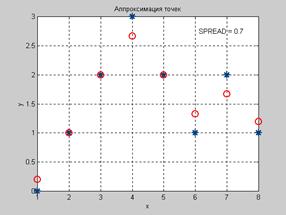 Рис. 6.12
Рис. 6.12 Рис. 6.13
Рис. 6.13 Рис. 6.14
Рис. 6.14 Рис. 6.15
Рис. 6.15