
|
|
В о п р о с ы д л я с а м о к о н т р о л я1. Цели динамического исследования и методы решения. 2. От каких факторов зависит выбор расчетной схемы? 3. Каковы критерии динамической устойчивости установок для оценки их работоспособности? 4. Какие основные факторы необходимо учитывать при структурном анализе конструкций современных образцов артиллерийских орудий с динамической точки зрения? 5. На какие свойства конструкции существенно влияют виброударные воздействия от выстрела? 6. Анализ характера действующих сил на образцы вооружения как динамических объектов; 7. Какое влияние на динамические характеристики образцов вооружения оказывает вид носителя и его особенности (наземные: ¾ буксируемые (рис.1.1); на сошниковых опорах;, ¾ самоходные (на колесном шасси, на гусеничном ходу); ¾ корабельные)и т.д.; 8. В чем особенности создания единой математической модели артиллерийского орудия при выстреле различных конструктивно - компоновочных схем?
Глава 2 ДВИЖЕНИЕ ПРИ НАЛИЧИИ СВЯЗЕЙ. УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА ПРИ НЕСТАЦИОНАРНОМ БАЗИСЕ
Основные понятияI j klmnopqrst {|} ¨ij έαβγεζηθξφχψωώ • "' æ ∂ T t r ŕ XYZ yz x'ýż ÿ ÝŻ Ÿ Vv w ẁ ẅ W Ẁ Ẅ Для изучения движения механических систем со связями, каковыми являются динамические объекты рассматриваемой нами дисциплины, в отличие от векторной механики Ньютона используются энергетические характеристики движения. Подчинение этих характеристик принципам аналитической механики позволяет получить наиболее общие формы как условий равновесия, так и дифференциальных уравнений движения механических систем. Наиболее удобными методами аналитической механики являются методы Лагранжа, основы которой были заложены им в его трактате «Аналитическая механика», опубликованном в 1788 г. Здесь Лагранж, подытожив все достижения механики того времени, вывел общие уравнения аналитической механики и дал методы решения конкретных задач. Назначение своего труда сам Лагранж характеризовал следующими словами: “ Я поставил себе целью свести теорию механики и методы решения связанных с нею задач к общим формулам, простое развитие которых даст все уравнения, необходимые для решения каждой задачи”. В состав рассматриваемых систем включены как материальные точки, так и абсолютно твердые тела. Системы материальных точек и тел условимся называть иногда для краткости просто «механическими системами».
§2.1. Несвободное движение точки. Механическая система, точки которой могут занимать любое положение в пространстве и иметь любые скорости, называется свободной. Например, свободной системой является космический аппарат, движущийся по орбите вокруг Земли. Его движение не ограничено другими телами и поэтому, прикладывая к аппарату соответствующие силы, можно изменять траекторию его центра масс и поворачивать аппарат вокруг центра масс. Если на координаты и скорости точек системы наложены ограничения, то система называется несвободной, а ограничения называются связями. Механические связи реализуются в виде различных устройств или тел (стержни, нити, шарниры и т.п.) Аналитически связь описывается уравнением вида
Здесь n –число материальных точек системы, положение которой в пространстве определяется 3n декартовыми координатами, и на которую наложено h связей Ограничивая движение механической системы, связи действуют на ее точки посредством сил, которые называются реакциями связей. При изучении равновесия и движения механических систем методами аналитической механики применяется принцип освобождения (аксиома о связях). Этот принцип состоит в том, что любую систему можно рассматривать как свободную, приложив к ее точкам реакции, соответствующие отброшенным связям. Они обычно выражаются в виде равенств или неравенств, в них может явно входить время и т. д.
Связи и их классификация
1. Связи называются голономными, если они описываются уравнениями вида
Такие связи накладывают ограничения на координаты точек, а значит, на положение системы в пространстве. Это так называемые геометрические связи. Вместе с тем голономные связи накладывают ограничения и на скорости точек системы. Соответствующие условия получаются в результате дифференцирования уравнений (2.1) по времени:
Голономные связи могут описываться и дифференциальными уравнениями, однако последние обязательно должны быть интегрируемыми.
Решение. Уравнения связей имеют вид
где j ¾ угол поворота диска (j = 0 при xc = 0). Рис.2.1Из первого уравнения связи следует, что
Интегрируя второе уравнение, находим связь между координатой xc и углом поворота диска Неголономными называются связи, которые описываются уравнениями вида
Уравнения (2.3), в отличие от уравнений голономных связей, не могут быть проинтегрированы независимо от дифференциальных уравнений движения системы. Неголономные связи накладывают ограничения (2.3) на скорости точек, поэтому их называют кинематическими.
Решение: Положение шара определяется координатами xc , yc , zc центра масс и тремя углами его поворота вокруг центра масс. Этими углами могут быть углы Эйлера. При любом положении шара расстояние от точки С Рис.2.2 до плоскости Оxy равно его радиусу. Поэтому одно из уравнений связи имеет вид zc = r. Другие уравнения связи определяются из условия качения без скольжения:
где СМЦС ¾ точка соприкосновения шара с плоскостью. Проецируя это векторное уравнение на оси неподвижной системы координат, получаем
Интегрирование последнего уравнения дает полученное выше геометрическое условие zc = r. Кинематические уравнения в проекциях на оси неподвижной системы координат имеют вид
Таким образом, уравнениями связей для шара являются
Первые два из них не интегрируются, т.е. являются уравнениями неголономных связей. 2. Связи подразделяются на стационарные и нестационарные в зависимости от того, входит в явном виде время в уравнение связи или нет. Связь, уравнение которой имеет вид
¾ является голономной и стационарной. Для голономной нестационарной связи уравнение имеет вид:
1. zM =0; 2. x2 + y2 - l2 =0.
Рис.2.3
1. zM =0; 2. x2 + y2 - l2 (t) £ 0.
Р Рис.2.4 3. Связь называют удерживающей (двухсторонней), если она описывается уравнением (равенством). На рис.2.3 уравнения связи описываются равенствами : 1. zM =0; 2. x2 + y2 - l2 =0. В этом случае говорят, что точка во все моменты времени должна оставаться на связи. Неудерживающая (односторонняя) связь описывается неравенством. Например, если математический маятник представляет собой тонкий стержень длиной l , вращающийся вокруг неподвижной оси и к свободному концу которого прикреплен груз (материальная точка), то связь для груза будет удерживающей. Если же груз прикреплен к свободному концу нерастяжимой нити длиной l, то связь будет неудерживающая, поскольку груз может находиться как на поверхности сферы радиусом l, так и внутри ее. x2 + y2 - l2 (t) £ 0

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

 (2.1)
(2.1) (2.2)
(2.2) Пример 2.1. Получить уравнения связей для диска радиусом r , который катится без скольжения по плоскости (рис.2.1).
Пример 2.1. Получить уравнения связей для диска радиусом r , который катится без скольжения по плоскости (рис.2.1).

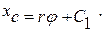
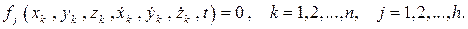 (2.3)
(2.3) Пример 2.2. Получить уравнения связей для шара радиусом r, который катится без скольжения по плоскости (рис.2.2)
Пример 2.2. Получить уравнения связей для шара радиусом r, который катится без скольжения по плоскости (рис.2.2)




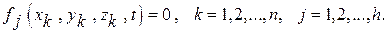
 Пример 2.3.Жесткий стержень длиной l , прикрепленный к неподвижной опоре и перемещающийся в плоскости xOy, (рис. 2.3)является стационарной связью для материальной точки М, находящейся на его свободном конце. Уравнения связи в декартовой системе координат, начало которой совпадает с точкой закрепления стержня, имеют вид
Пример 2.3.Жесткий стержень длиной l , прикрепленный к неподвижной опоре и перемещающийся в плоскости xOy, (рис. 2.3)является стационарной связью для материальной точки М, находящейся на его свободном конце. Уравнения связи в декартовой системе координат, начало которой совпадает с точкой закрепления стержня, имеют вид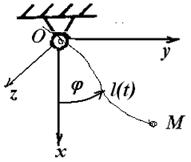 Пример 2.4.Если длина стержня изменяется по заданному закону (рис. 2.4), то связь является нестационарной и уравнения связей имеют вид:
Пример 2.4.Если длина стержня изменяется по заданному закону (рис. 2.4), то связь является нестационарной и уравнения связей имеют вид: