
|
|
Понятие об автомодельности.Автомодельность - кардинальное понятие теории подобия, принципиальное содержание которого сводится к так называемому вырождению чисел подобия. Формальным признаком её служит выпадение чисел подобия как аргументов, входящих в функциональную зависимость. Обстоятельное рассмотрение этого вопроса можно найти в книге А.А.Гухмана «Применение теории подобия к исследованию процессов тепломассообмена. Процессы переноса в движущейся среде». - М.: Высшая шкала,1967. - 302 с. Мы же ограничимся лишь кратким рассмотрением содержания этого понятия без уяснения которого невозможна грамотная постановка эксперимента. Для простоты будем считать, что в интересующем исследователя процессе определяющими является силы вязкого трения т.е. зависимость (13.8) имеет вид
Как следует из рисунка, при увеличении числа Рейнольдса в опытах зависимость
Исчезновение (вырождение) числа Рейнольдса означает отсутствие предпосылок для подобия . Очевидно, механизм процесса таков, что не надо никаких условий для подобия и все процессы такого типа автоматически подобны между собой. Этот случай и называется автомодельностью. На рис.13.1 автомодельная область обозначена римской цифрой II. В общем случае под автомодельной понимают область, в которой неопределяющее число подобия перестает зависеть от определяющего (либо определяющих). Проведение опытов в этой области существенно упрощается. Действительно, если в области I экспериментатор должен заботиться о том, чтобы Таким образом, приведенные сведения показывают, что если в результате анализа изучаемого явления удается составить его математическую модель, то принципиально задача постановки эксперимента может считаться разрешенной. К сожалению, возможность аналитического описания является скорее исключением, чем правилом. Поэтому целью следующего раздела является ознакомление со стратегией исследователя при возникновении такой ситуации. Анализ размерностей. Следует подчеркнуть, что конечная цель в рассматриваемом случае остается прежней: нахождение чисел подобия, по которым следует вести моделирование, но решается она при существенно меньшем объеме информации о характере процесса. Для уяснения дальнейшего кратко рассмотрим некоторые основополагающие понятия. Обстоятельное изложение можно найти в книге А.Н.Лебедева «Моделирование в научно-технических исследованиях». - М.: Радио и связь. 1989. -224 с. Любой материальный объект обладает рядом свойств, которые допускают количественное выражение. При этом каждое из свойств характеризуется размером определенной физической величины. Единицы некоторых физических величин можно выбирать произвольно, и с их помощью представлять единицы всех остальных. Физические единицы, выбираемые произвольно, называют основными. В международной системе (применительно к механике) это - килограмм, метр и секунда. Остальные величины, выраженные через эти три, называют производными. Основная единица может обозначаться либо символом соответствующей величины, либо специальным символом. Например, единицы длины - L, единицы массы - M, единица времени - T. Либо, единица длины - метр (м), единица массы - килограмм (кг), единица времени - секунда (с). Под размерностью понимают символическое выражение (иногда его называют формулой) в виде степенного одночлена, связывающее производную величину с основными. Общий вид этой закономерности имеет вид
где x, y, z- показатели размерности. Например, размерность скорости
Для безразмерной величины все показатели Два следующих утверждения достаточно ясны и не нуждаются в каких-либо специальных доказательствах. Отношение размеров двух объектов является величиной постоянной вне зависимости от того, в каких единицах они выражаются. Так, например, если отношение площади, занимаемой окнами, к площади стен составляет 0,2, то этот результат останется неизменным, если сами площади выражать в мм2, м2или км2. Второе положение можно сформулировать следующим образом. Любое правильное физическое соотношение должно быть размерностно однородным. Это означает, что все члены, входящие как в правую, так и в левую его части должны иметь одинаковую размерность. Это простое правило четко реализуется в житейском обиходе. Все осознают, что метры можно складывать только с метрами и никак не с килограммами или с секундами. Нужно четко представлять, что правило остается справедливым и при рассмотрении даже самых сложных уравнений. Метод анализа размерностей базируется на так называемой Любая функциональная зависимость между размерными величинами может быть представлена в виде зависимости между N безразмерными комплексами (числами Пусть, например, величина А является функцией пяти размерных величин (
Из
где Эту теорему иногда приписывают Бэкингему и называют Доказательство теоремы выходит за рамки курса. При необходимости оно может быть найдено в книге Л.И.Седова «Методы подобия и размерностей в механике» - М.: Наука, 1972. - 440 с. Подробное обоснование метода приводится и в книге В.А.Веникова и Г.В.Веникова «Теория подобия и моделирования» - М.: Высшая школа, 1984. -439 с. Особенностью этой книги является то, что помимо вопросов, связанных с подобием, в нее включены сведения о методике постановки эксперимента и обработки его результатов. Использование анализа размерностей для решения конкретных практических задач связано с необходимостью составления функциональной зависимости вида (13.12), которая на следующем этапе обрабатывается специальными приемами, приводящими в конечном итоге к получению чисел Основным, носящим творческий характер, является первый этап, так как получаемые результаты зависят от того, насколько правильно и полно представление исследователя о физической природе процесса. Другими словами, насколько функциональная зависимость (13.12) правильно и полно учитывает все параметры, влияющие на изучаемый процесс. Любая ошибка здесь неизбежно приводит к ошибочным выводам. В истории науки известна так называемая «ошибка Рэлея». Суть ее в том, что изучая задачу о теплообмене при турбулентном течении, Рэлей не учел влияние вязкости потока, т.е. не включил её в зависимость (13.12). В результате в конечные соотношения, полученные им, не вошло число подобия Рейнольдса, играющее исключительно важную роль в теплообмене. Для уяснения сущности метода рассмотрим пример, иллюстрирующий как общий подход к задаче, так и способ получения чисел подобия. Необходимо установить вид зависимости, позволяющий определить потери давления либо напора при турбулентном течении в круглых трубах. Напомним, что эта задача уже рассматривалась в разделе 12.6. Поэтому представляет несомненный интерес установить, как она может быть разрешена с помощью анализа размерностей и дает ли это решение какую-то новую информацию. Ясно, что падение давления вдоль трубы, обусловленное затратами энергии на преодоление сил вязкого трения обратно пропорционально её длине, поэтому с целью сокращения числа переменных целесообразно рассматривать не Из представлений о физической сущности процесса можно предположить что возникающие потери должны зависеть: от средней скорости течения рабочей среды (v); от размера трубопровода, определяемого его диаметром (d); от физических свойств транспортируемой среды, характеризуемых её плотностью (
либо
На этом и заканчивается первый и, нужно подчеркнуть, наиболее ответственный этап анализа размерностей. В соответствии с
Существует несколько способов нахождения чисел Основным достоинством его является то, что он представляет собой своеобразный алгоритм, приводящий к решению задачи. Из параметров, входящих в (13.15) необходимо выбрать три любых, но так, чтобы в них входили основные единицы, т.е. метр, килограмм и секунда. Пусть ими будут v, d, Образуются числа
Теперь задача сводится к нахождению всех показателей степеней. При этом они должны быть подобраны так, чтобы числа Для решения этой задачи определим прежде всего размерности всех параметров:
Вязкость Параметр И, наконец, Таким образом, размерности чисел
либо
Аналогично два других
В начале раздела 13.3 уже отмечалось, что для любой безразмерной величины показатели размерности
Приравнивая показатели степеней, получаем три уравнения с тремя неизвестными
Откуда находим Подставляя эти значения в ( 13.6), получаем
Действуя аналогично, легко показать, что
Таким образом, зависимость (13.15) принимает вид
Так как
либо
Следует иметь в виду, что анализ размерностей не дает и принципиально не может дать каких-то числовых значений в получаемых с его помощью соотношениях. Поэтому он должен завершаться анализом результатов и при необходимости их корректировкой, исходя из общих физических представлений. Рассмотрим с этих позиций выражение (13.21). В правую его часть входит квадрат скорости, но эта запись не выражает ничего, кроме того, что скорость возводится в квадрат. Однако, если поделить эту величину на два, т.е.
Если теперь, как в (12.26), обозначить
либо
где
ЛИТЕРАТУРА 1.Кальницкий Л.А., Добротин Д.А., Жевержеев В.Ф. Специальный курс высшей математики для втузов. М.:Высшая школа, 1976. - 389с. 2.Астарита Дж., Марручи Дж. Основы гидромеханики неньютоновских жидкостей. - М.: Мир, 1978.-307с. 3.Федяевский К.К., Фаддеев Ю.И. Гидромеханика. - М.: Судостроение, 1968. - 567 с. 4.Фабрикант Н.Я. Аэродинамика. - М.: Наука, 1964. - 814 с. 5.Аржаников Н.С. и Мальцев В.Н. Аэродинамика. - М.: Оборонгиз, 1956 - 483 с. 6.Фильчаков П.Ф. Приближенные методы конформных отображений. - К.: Наукова думка, 1964. - 530 с. 7.Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. - М.: Наука, 1987. - 688 с. 8.Дейли Дж., Харлеман Д. Механика жидкости. -М.: Энергия, 1971. - 480 с. 9.А.С. Монин , А.М. Яглом «Статистическая гидромеханика» (ч.1. -М.: Наука, 1968. -639 с.) 10.Шлихтинг Г. Теория пограничного слоя. - М.: Наука, 1974. - 711 с. 11.Павленко В.Г. Основы механики жидкости. - Л.: Судостроение, 1988. - 240 с. 12.Альтшуль А.Д. Гидравлические сопротивления. - М.: Недра, 1970. - 215 с. 13.А.А.Гухман «Введение в теорию подобия». - М.: Высшая школа, 1963. - 253 с. 14.С. Клайн «Подобие и приближенные методы». - М.: Мир, 1968. - 302 с. 15.А.А.Гухман «Применение теории подобия к исследованию процессов тепломассообмена. Процессы переноса в движущейся среде». - М.: Высшая шкала,1967. - 302 с. 16.А.Н.Лебедев «Моделирование в научно-технических исследованиях». - М.: Радио и связь. 1989. -224 с. 17.Л.И.Седов «Методы подобия и размерностей в механике» - М.: Наука, 1972. - 440 с. 18.В.А.Веников и Г.В.Веников «Теория подобия и моделирования» - М.: Высшая школа, 1984. -439 с.
ОГЛАВЛЕНИЕ 1. МАТЕМАТИЧЕСКИЙ АППАРАТ, ИСПОЛЬЗУЕМЫЙ В МЕХАНИКЕ ЖИДКОСТИ................................................................................................ 3 1.1. Векторы и операции над ними................................................... 4 1.2. Операции первого порядка (дифференциальные характеристики поля). ......................................................................................................... 5 1.3. Операции второго порядка........................................................ 6 1.4. Интегральные соотношения теории поля.................................. 7 1.4.1. Поток векторного поля.................................................. 7 1.4.2. Циркуляция вектора поля.............................................. 7 1.4.3. Формула Стокса............................................................. 7 1.4.4. Формула Гаусса-Остроградского.................................. 7 2. ОСНОВНЫЕ ФИЗИЧЕСКИЕ СВОЙСТВА И ПАРАМЕТРЫ ЖИДКОСТИ. СИЛЫ И НАПРЯЖЕНИЯ........................................................................... 8 2.1. Плотность.................................................................................... 8 2.2. Вязкость....................................................................................... 9 2.3. Классификация сил.................................................................... 12 2.3.1. Массовые силы............................................................. 12 2.3.2. Поверхностные силы.................................................... 12 2.3.3. Тензор напряжения...................................................... 13 2.3.4. Уравнение движения в напряжениях........................... 16 3. ГИДРОСТАТИКА................................................................................. 18 3.1. Уравнение равновесия жидкости.............................................. 18 3.2. Основное уравнение гидростатики в дифференциальной форме. ......................................................................................................... 19 3.3. Эквипотенциальные поверхности и поверхности равного давления. ......................................................................................................... 20 3.4. Равновесие однородной несжимаемой жидкости в поле сил тяжести. Закон Паскаля. Гидростатический закон распределения давления... 20 3.5. Определение силы давления жидкости на поверхности тел.... 22 3.5.1. Плоская поверхность.................................................... 24 4. КИНЕМАТИКА..................................................................................... 26 4.1. Установившееся и неустановившееся движение жидкости...... 26 4.2. Уравнение неразрывности (сплошности)................................. 27 4.3. Линии тока и траектории.......................................................... 29 4.4. Трубка тока (поверхность тока)............................................... 29 4.5. Струйная модель потока........................................................... 29 4.6. Уравнение неразрывности для струйки................................... 30 4.7. Ускорение жидкой частицы...................................................... 31 4.8. Анализ движения жидкой частицы........................................... 32 4.8.1. Угловые деформации................................................... 32 4.8.2. Линейные деформации................................................. 36 5. ВИХРЕВОЕ ДВИЖЕНИЕ ЖИДКОСТИ.............................................. 38 5.1. Кинематика вихревого движения............................................. 38 5.2. Интенсивность вихря................................................................ 39 5.3. Циркуляция скорости............................................................... 41 5.4. Теорема Стокса......................................................................... 42 6. ПОТЕНЦИАЛЬНОЕ ДВИЖЕНИЕ ЖИДКОСТИ................................ 44 6.1. Потенциал скорости.................................................................. 44 6.2. Уравнение Лапласа................................................................... 46 6.3. Циркуляция скорости в потенциальном поле.......................... 47 6.4. Функция тока плоского течения............................................... 47 6.5. Гидромеханический смысл функции тока................................ 49 6.6. Связь потенциала скорости и функции тока............................ 49 6.7. Методы расчета потенциальных потоков................................ 50 6.8. Наложение потенциальных потоков......................................... 54 6.9. Бесциркуляционное обтекание круглого цилиндра................ 58 6.10. Применение теории функций комплексного переменного к изучению плоских потоков идеальной жидкости............................................ 60 6.11. Конформные отображения..................................................... 62 7. ГИДРОДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ............................. 65 7.1. Уравнения движения идеальной жидкости.............................. 65 7.2. Преобразование Громеки-Лэмба............................................. 66 7.3. Уравнение движения в форме Громеки-Лэмба........................ 67 7.4. Интегрирование уравнения движения для установившегося течения ......................................................................................................... 68 7.5. Упрощенный вывод уравнения Бернулли............................... 69 7.6. Энергетический смысл уравнения Бернулли........................... 70 7.7. Уравнение Бернулли в форме напоров.................................... 71 8. ГИДРОДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ..................................... 72 8.1. Модель вязкой жидкости.......................................................... 72 8.1.1. Гипотеза линейности ................................................... 72 8.1.2. Гипотеза однородности................................................ 74 8.1.3. Гипотеза изотропности................................................. 74 8.2 Уравнение движения вязкой жидкости. (уравнение Навье-Стокса) ......................................................................................................... 74 9. ОДНОМЕРНЫЕ ТЕЧЕНИЯ НЕСЖИМАЕМОЙ ЖИДКОСТИ (основы гидравлики)........................................................................................................... 77 9.1. Расход потока и средняя скорость........................................... 77 9.2. Слабодеформированные потоки и их свойства....................... 78 9.3. Уравнение Бернулли для потока вязкой жидкости................. 79 9.4. Физический смысл коэффициента Кориолиса......................... 82 10. КЛАССИФИКАЦИЯ ТЕЧЕНИЙ ЖИДКОСТИ. УСТОЙЧИВОСТЬ ДВИЖЕНИЯ.............................................................................................. 84 11. ЗАКОНОМЕРНОСТИ ЛАМИНАРНОГО РЕЖИМА ТЕЧЕНИЯ В КРУГЛЫХ ТРУБАХ..................................................................................................... 86 12. ОСНОВНЫЕ ЗАКОНОМЕРНОСТИ ТУРБУЛЕНТНОГО ДВИЖЕНИЯ. .................................................................................................................. 90 12.1. Общие сведения....................................................................... 90 12.2. Уравнения Рейнольдса............................................................ 92 12.3. Полуэмпирические теории турбулентности.......................... 93 12.4. Турбулентное течение в трубах............................................. 95 12.5. Степенные законы распределения скоростей....................... 100 12.6. Потери давления (напора) при турбулентном течении в трубах. ......................................................................................................... 100 13. ОСНОВЫ ТЕОРИИ ПОДОБИЯ И МОДЕЛИРОВАНИЯ............... 102 13.1. Инспекционный анализ дифференциальных уравнений..... 106 13.2. Понятие об автомодельности................................................ 110 13.3. Анализ размерностей............................................................ 111
Литература …………………………………………………………………..118

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . График этой зависимости устанавливается экспериментально, и часто имеет вид, показанный на рис. 13.1.
. График этой зависимости устанавливается экспериментально, и часто имеет вид, показанный на рис. 13.1.

 ) происходит «вырождение», т.е. число Эйлера перестает зависеть от Re.
) происходит «вырождение», т.е. число Эйлера перестает зависеть от Re. , что далеко не всегда возможно, то в автомодельной области достаточно, чтобы
, что далеко не всегда возможно, то в автомодельной области достаточно, чтобы  было больше
было больше  . Нужно лишь помнить, что какого-то универсального значения
. Нужно лишь помнить, что какого-то универсального значения  не существует, оно всегда зависит от природы изучаемого объекта, в частности, от его формы. Поэтому, как правило, задачей первого этапа экспериментального исследования является нахождение граничного значения определяющего числа подобия.
не существует, оно всегда зависит от природы изучаемого объекта, в частности, от его формы. Поэтому, как правило, задачей первого этапа экспериментального исследования является нахождение граничного значения определяющего числа подобия. (13.11)
(13.11)
 , и, следовательно,
, и, следовательно,  .
. -теореме (читается: пи-теорема).
-теореме (читается: пи-теорема).  , где n - число основных единиц. Как уже отмечалось выше, в гидромеханике
, где n - число основных единиц. Как уже отмечалось выше, в гидромеханике  (кг, м, с).
(кг, м, с). ), т.е.
), т.е. (13.12)
(13.12)
 )
) (13.13)
(13.13) и
и  - безразмерные комплексы, составленные из размерных величин.
- безразмерные комплексы, составленные из размерных величин.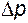 , а
, а  , т.е. потери давления на единицу длины трубы. Напомним, что отношение
, т.е. потери давления на единицу длины трубы. Напомним, что отношение 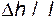 , где
, где  - потери напора, носит название гидравлического уклона.
- потери напора, носит название гидравлического уклона.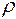 ) и вязкостью (
) и вязкостью ( 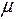 ); и, наконец, разумно считать, что потери должны быть как-то связаны с состоянием внутренней поверхностью трубы, т.е. с шероховатостью (k) ее стенок. Таким образом, зависимость (13.12) в рассматриваемом случае имеет вид
); и, наконец, разумно считать, что потери должны быть как-то связаны с состоянием внутренней поверхностью трубы, т.е. с шероховатостью (k) ее стенок. Таким образом, зависимость (13.12) в рассматриваемом случае имеет вид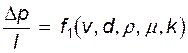
 (13.14)
(13.14) . Следовательно, число безразмерных комплексов
. Следовательно, число безразмерных комплексов  , т.е. после соответствующей обработки (13.14) должна принять вид
, т.е. после соответствующей обработки (13.14) должна принять вид (13.15)
(13.15)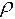 . Легко убедиться, что они удовлетворяют поставленному требованию.
. Легко убедиться, что они удовлетворяют поставленному требованию. ; (13.16)
; (13.16)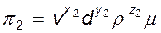 ; (13.17)
; (13.17)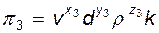 ; (13.18)
; (13.18) ;
;  ;
; 
 , т.е.
, т.е.  .
.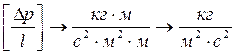 , и
, и  .
. .
.

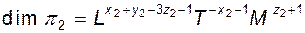


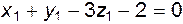
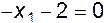

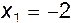 ;
; 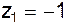 ;
; 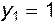 .
.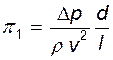 (13.19)
(13.19) и
и 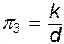 .
.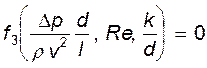 (13.20)
(13.20)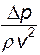 есть неопределяющее число подобия (число Эйлера), то (13.20) можно записать как функциональную зависимость
есть неопределяющее число подобия (число Эйлера), то (13.20) можно записать как функциональную зависимость
 (13.21)
(13.21) , то как известно из гидромеханики, она приобретает важный физический смысл: удельной кинетической энергии, а
, то как известно из гидромеханики, она приобретает важный физический смысл: удельной кинетической энергии, а  - динамическое давление, обусловленное средней скоростью. С учетом этого (13.21) целесообразно записать в виде
- динамическое давление, обусловленное средней скоростью. С учетом этого (13.21) целесообразно записать в виде (13.22)
(13.22) буквой
буквой  , то приходим к формуле Дарси
, то приходим к формуле Дарси (13.23)
(13.23) (13.24)
(13.24)