
|
|
Установившееся и неустановившееся движения жидкости.Установившимся (стационарным) называют движение, при котором основные параметры потока (скорость, давление, плотность) в данной точке пространства не изменяются с течением времени, т.е.
Если это условие не соблюдается и параметры в точке меняются с течением времени
движение называют неустановившимся (нестационарным). В этих формулировках следует обратить внимание на то, что речь идет о параметрах в точке. Чтобы уяснить это, рассмотрим канал, показанный на рис. 4.1. В гидромеханике такие каналы, в которых площадь сечения уменьшается по ходу потока, называют конфузорами. Исходя из чисто интуитивных представлений ясно, что скорость течения по ходу канала будет возрастать. Возникает вопрос, может ли быть установившемся движение в таком канале. Очевидно, может, если параметры в точках A и B не будут изменяться с течением времени. Определение вида движения не требует, чтобы параметры в точках А, В и С были одинаковы. Уравнение неразрывности (сплошности). Уравнение неразрывности либо сплошности выражает один из фундаментальных законов природы - закон сохранения массы применительно к жидкой среде.
Рассмотрим объем V, ограниченный поверхностью S (рис. 4.2). Выделим элемент поверхности dS. Пусть
(знак минус, т.к. направления
С другой стороны, приток жидкости в объем приводит к изменению ее массы. При этом, поскольку выделенный объем является постоянным, изменение массы может происходить только за счет изменения ее плотности. Скорость изменения массы можно представить как
либо с учетом того, что
Очевидно, что изменение массы внутри объема должно быть равно массе, поступившей в него извне, т.е.
Применяя преобразование Гаусса-Остроградского, получим:
Равенство нулю интеграла возможно лишь при условии
Это и есть уравнение неразрывности. Поскольку при выводе его не делалось никаких ограничений, то оно справедливо как для установившегося, так и для неустановившегося движений сжимаемой и несжимаемой жидкости. Уравнение (4.3) относится к числу фундаментальных уравнений механики жидкости. Рассмотрим некоторые частные случаи. При установившемся движении все производные по времени равны нулю, что следует из самого определения этого понятия, поэтому
Если движение установившееся и жидкость несжимаема, т.е.
Либо в проекциях на декартовы оси координат (см. формулу 1.7)
Установим физический смысл этого соотношения. Частные производные Как уже отмечалось в 1.1, поле, в котором Линии тока и траектории. Линией тока называется кривая, обладающая тем свойством, что в данный момент времени векторы скоростей в любой ее точке совпадают по направлению с касательными. В векторной форме это условие может быть записано как
Раскрывая определитель, получаем дифференциальное уравнение линии тока в виде
Под траекторией понимается след, оставленный движущейся частицей в пространстве. Дифференциальное уравнение траектории
Из сопоставления (4.8) и (4.9) следует, что в общем случае, т.е. при неустановившемся движении, линии тока и траектории не совпадают. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
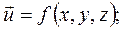

 (4.1)
(4.1)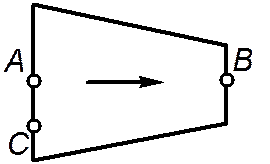
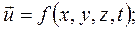
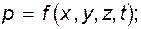 (4.2)
(4.2)
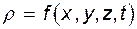

 - орт внешней нормали, а
- орт внешней нормали, а  - вектор скорости. Через выделенный элемент dS в единицу времени внутрь объема проникает масса жидкости
- вектор скорости. Через выделенный элемент dS в единицу времени внутрь объема проникает масса жидкости .
.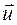 и
и  противоположны). Секундная масса, проникающая в объем через всю поверхность,
противоположны). Секундная масса, проникающая в объем через всю поверхность, .
.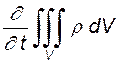 ,
, , можно записать
, можно записать .
.
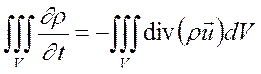 , либо
, либо .
. . (4.3)
. (4.3) . (4.4)
. (4.4) , то
, то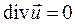 . (4.5)
. (4.5) . (4.6)
. (4.6) ,
,  ,
,  характеризуют скорость относительного удлинения (укорочения) жидкой частицы. Если этот процесс происходит одновременно вдоль всех координатных осей, то он приводит к объемному расширению либо сжатию частицы. Ясно, что если частица удлиняется вдоль осей x и y, то она должна укорачиваться относительно оси z. Другими словами, хотя бы одна из производных, входящих в (4.6), должна быть отрицательна, т.к. в противном случае соотношение не может быть равным нулю.
характеризуют скорость относительного удлинения (укорочения) жидкой частицы. Если этот процесс происходит одновременно вдоль всех координатных осей, то он приводит к объемному расширению либо сжатию частицы. Ясно, что если частица удлиняется вдоль осей x и y, то она должна укорачиваться относительно оси z. Другими словами, хотя бы одна из производных, входящих в (4.6), должна быть отрицательна, т.к. в противном случае соотношение не может быть равным нулю.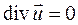 , носит название соленоидального.
, носит название соленоидального. , т.е. векторное произведение должно быть равно нулю. Это, как известно (см. формулу 1.4), может быть записано в виде определителя
, т.е. векторное произведение должно быть равно нулю. Это, как известно (см. формулу 1.4), может быть записано в виде определителя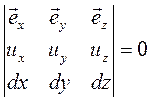 (4.7)
(4.7)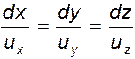 (4.8)
(4.8) (4.9)
(4.9)