
|
|
ГИДРОДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИВ механике жидкости понятию «гидродинамика» придается весьма широкий смысл. В настоящем пособии этот термин будет использоваться в его классическом значении, как раздел курса, который, в отличие от кинематики, рассматривающей движение жидкости без учета причин, обусловивших его, изучает как само движение, так и причины, приводящие к его возникновению. Движение жидкости вызывается действием сил, а если иметь в виду, что давление есть частное от деления силы на площадь, то можно считать, что причиной возникновения движения частиц с какими-то скоростями является разность (перепад) давлений. Таким образом, для расчета течений необходимо иметь уравнение, связывающее давление в точке со скоростью движения частицы. Уравнения движения идеальной жидкости. Уравнения движения идеальной жидкости можно получить из уравнений движения в напряжениях, положив в них все производные от
либо в векторной форме
Система (7.1) называется системой дифференциальных уравнений Эйлера для гидродинамики, она связывает давления и скорости в движущейся жидкости. Следует помнить, что выражения в правой части уравнений системы являются полными либо субстанциональными производными. Наличие конвективных членов ускорения приводит к тому, что система является нелинейной, содержащей четыре неизвестных: три проекции скорости и давление. Проекции единичных массовых сил обычно известны из постановки задачи. Три уравнения (7.1) плюс уравнение неразрывности образуют замкнутую систему. Преобразование Громеки-Лэмба. Рассмотрение теоремы Гельмгольца о движении жидкой частицы показывает, что жидкость как любое материальное тело может участвовать в поступательном и вращательном движениях. Следует обратить внимание на то, что для совершения работы в современных технических устройствах может использоваться только энергия поступательного движения. Энергия же вращательного (вихревого) движения полностью теряется, рассеивается в окружающей среде, превращаясь в теплоту. Система уравнений Эйлера (7.4) не учитывает факт существования этих двух движений, что в определенной степени обедняет ее. Поэтому целесообразно использовать преобразование, позволяющее учесть эту особенность движения жидких частиц, называемое преобразованием Громеки-Лэмба. Формально оно сводится к тому, что в выражение для ускорения вводятся члены, характеризующие вращение жидких частиц. Рассмотрим лишь одну компоненту:
Прибавим и вычтем в конвективной части ускорения выражение
Скомпонуем члены с учетом знаков:
Выражения в скобках есть не что иное, как удвоенные компоненты вихря
Подставляя полученные значения в (7.3) имеем
и по аналогии
В векторной форме выражение для ускорения будет иметь вид:
Если движение установившееся, то
Уравнение движения в форме Громеки-Лэмба. Если в (7.2) в правую часть подставить ускорение в виде (7.7) либо (7.8), то это приводит к уравнению движения в форме Громеки-Лэмба. Для установившегося движения имеем
Выполним некоторые преобразования (7.9). В разделе гидростатики было введено понятие о скалярной функции , называемой силовой. Было показано, что
Поскольку эта функция является полным дифференциалом, то можно записать
Сопоставляя (7.10) и (7.11), получаем
С другой стороны вектор
Из (7.12) и (7.13) следует, что
С учетом (7.14) выражение (7.9) принимает вид
Следует иметь в виду, что эта форма записи справедлива лишь для несжимаемой жидкости, т.е. при условии
Опуская эту операцию, которую обучающийся при желании может выполнить самостоятельно, приведем лишь конечный результат

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
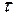 равными нулю и заменив нормальные напряжения давлениями, имея в виду, что
равными нулю и заменив нормальные напряжения давлениями, имея в виду, что  . Таким образом, уравнения гидродинамики принимают вид
. Таким образом, уравнения гидродинамики принимают вид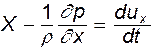
 (7.1)
(7.1)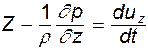
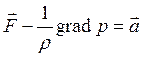 (7.2)
(7.2) (7.3)
(7.3)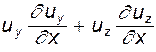
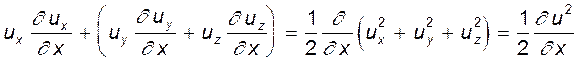
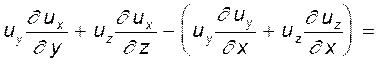
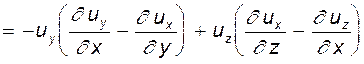
 и
и  , т.е. можем записать
, т.е. можем записать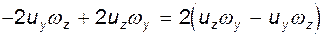
 (7.4)
(7.4) (7.5)
(7.5) (7.6)
(7.6) (7.7)
(7.7) (7.8)
(7.8) (7.9)
(7.9) (7.10)
(7.10) (7.11)
(7.11)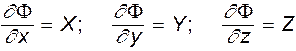 (7.12)
(7.12) , проекциями которого являются X, Y, и Z
, проекциями которого являются X, Y, и Z (7.13)
(7.13)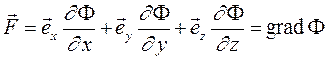 (7.14)
(7.14) (7.15)
(7.15) . И, наконец, уравнению движения (7.15) можно придать более удобную для анализа форму, умножив скалярно его левую и правую части на произвольный направленный отрезок
. И, наконец, уравнению движения (7.15) можно придать более удобную для анализа форму, умножив скалярно его левую и правую части на произвольный направленный отрезок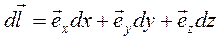 (7.16)
(7.16) (7.17)
(7.17)