
|
|
Инспекционный анализ дифференциальных уравнений.Исходим из того, что математическая модель процесса нам известна, но она не может быть проинтегрирована. В этом случае числа подобия могут быть найдены методом, который по предложению известного американского математика и гидродинамика Г.Биркгофа назван инспекционным анализом. Как следует из названия, метод заключается в организованном по определенным правилам «инспектировании» дифференциальных уравнений, которое должно выявить числа подобия, позволяющие моделировать процесс. Отметим лишь, что этот метод не является единственным. Интересующиеся другими подходами могут найти их в книге Я.М. Брайниса «Подобие и моделирование в химической и нефтехимической технологии».-М.: Гостоптехиздат, 1961. - 219 с. Базой инспекционного анализа является положение, рассматриваемое как постулат и сводящееся к следующему. Если две системы описываются одинаковыми дифференциальными уравнениями и имеют одинаковые граничные условия, и если значения всех параметров в этих уравнениях и граничных уравнениях равны, то эти две системы подобны, при условии существования единственности решения. Желающие познакомиться с подробным анализом всех элементов, входящих в это утверждение могут обратиться к превосходной книге А.А.Гухмана «Введение в теорию подобия». - М.: Высшая школа, 1963. - 253 с. В данном пособии мы примем его как постулат, опуская все обоснования. Вторая его половина относится к так называемым условиям однозначности. Это крайне важное понятие требует более внимательного рассмотрения. Любое дифференциальное уравнение описывает целый класс явлений, т.е. решение их многозначно. Так, например, то же уравнение Навье-Стокса, к которому мы уже неоднократно возвращались, может описывать движение жидкости в каналах, реках и океанах, движение атмосферных масс воздуха и т.п. Инженера интересует конкретное явление данного класса. Поэтому из множества возможных решений требуется лишь одно, соответствующее изучаемому явлению. Этого можно добится, если при постановке задачи ввести дополнительные так называемые условия однозначности, которые включают: - данные о физических свойствах среды (плотность, вязкость); - сведения о начальном состоянии системы (начальные условия); - данные о поведении системы на её границах (граничные условия). Инспекционный анализ представляет собой определенный алгоритм, включающий два этапа: на первом из них отношение дифференциальных величин заменяются отношениями самих переменных, на втором - уравнение приводится к безразмерному виду путем деления всех его членов на один из них, выбранный произвольно. Метод наиболее просто усвоить, обратившись к рассмотрению конкретного примера. Имея в виду, что в механике жидкости основными соотношениями, описывающими движение вязких сред, являются уравнения Навье-Стокса, целесообразно воспользоваться именно ими. Рассмотрим одну из проекций в декартовой системе координат. В данном случае безразлично какую, так как структура уравнений одинакова, что обеспечит и одинаковость получаемых результатов. В проекции на ось x-ов имеем
Будем считать, что из массовых сил действует только сила тяжести, т.е.
В такой форме записи каждый из членов выражает силу, отнесенную к единице объема. При этом
Действуя по алгоритму, заменим дифференциальные соотношения отношениями величин. Имеем:
Приводим эти соотношения к безразмерному виду, приняв в качестве делителя один из комплексов. Как отмечалось выше, он может быть выбран произвольно. Пусть им будет
Следует отметить, что вопрос о правильности интерпретации чисел подобия как отношения сил ставился рядом исследователей. По некоторым сведениям, еще Прандтль высказывал мнение о том, что число Рейнольдса не всегда равно отношению силы инерции к силе внутреннего трения. Более точным и правильным является утверждение, что если две системы геометрически подобны и течение в них происходят при одинаковых числах Рейнольдса, то отношение сил инерции к силам трения для обоих потоков одинаково. Подробности, связанные с таким подходом можно найти в книге С. Клайна «Подобие и приближенные методы». - М.: Мир, 1968. - 302 с. Таким образом, при моделировании гидромеханических явлений необходимо использовать числа подобия Струхаля, Фруда, Рейнольдса и Эйлера. Анализируя величины, входящие в числа подобия, легко заметить, что они составлены из параметров, входящих в условия однозначности. Эти числа подобия называют определяющими. Экспериментатор, разумеется, в определенных пределах, может изменять их величину ( менять скорость, геометрические размеры, вязкость). В число Эйлера входит величина
Если изучается установившееся движение, при котором параметры в точке не изменяются с течением времени, то из рассмотрения выпадает число Струхаля и
Следовательно, при моделировании гидромеханических явлений в данном случае должны соблюдаться следующие условия, обеспечивающие динамическое подобие:
либо
Если при проведении опытов удается соблюсти эти требования, то подобие называется полным. Однако в реальных условиях добиться этого достаточно трудно, а иногда и просто невозможно. Поэтому обычно ограничиваются частичным подобием. Анализируя сущность явления экспериментатор устанавливает какие из сил (тяжести, трения) играют определяющую роль в исследуемом процессе и моделирует только их. В этом случае при установившемся движении зависимость (13.9) распадается на две
из которых и выбирается определяющая. Дополнительно отметим, что для сжимаемых сред в число определяющих чисел подобия помимо полученных выше входит и число Маха. Остается открытым лишь вопрос о кинематическом подобии. Опыт многочисленных исследований показывает, что для его решения не требуется каких-либо специальных мер. Если системы динамически подобны и течение происходит в геометрически подобных каналах, то кинематическое подобие обеспечивается автоматически. Кратко остановимся еще на двух вопросах, носящих принципиальный характер. Первый из них связан с понятием геометрического подобия «в большом» и «малом». В начале раздела было показано, что геометрическое подобие натуры и модели может быть легко реализовано. Подобие геометрических границ объектов относится к подобию «в большом». Вместе с тем стенки каналов как натуры, так и модели имеют какую-то шероховатость. Очевидно, что моделирование шероховатости практически невозможно, и геометрическое подобие «в малом» недостижимо. Второй вопрос связан с так называемым «масштабным эффектом». Суть его в том, что моделирование, основанное на классических принципах теории подобия, не обеспечивает масштабный переход. Это означает, что эффективность различного рода промышленных технологических аппаратов оказывается ниже той, которая должна была бы быть по результатам, полученным пересчетом с модельных испытаний. Более того, она ухудшается по мере увеличения размеров аппаратов. Это вынуждает исследователей отказываться от испытаний на моделях и переходу к испытаниям на объектах, построенных в натуральную величину, что резко повышает стоимость эксперимента, а при создании особо крупных аппаратов такой подход вообще невозможно реализовать. Исследования, выполненные в последние годы, показали, что в основе масштабного эффекта лежат чисто гидродинамические явления: неравномерность распределения потоков по сечению аппарата, увеличение масштаба турбулентности и т.п., что позволяет найти способы устранения этого эффекта. Достаточно полное изложение теории можно найти в книге под ред. А.М.Розена «Масштабный переход в химической технологии: разработка промышленных аппаратов методом гидродинамического моделирования»: Химия, 1980. - 320 с. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
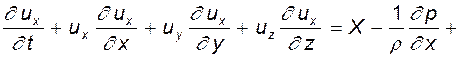
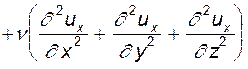
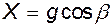 (
( 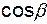 учитывает знак). С учетом этого и после умножения всех членов уравнения на плотность получим
учитывает знак). С учетом этого и после умножения всех членов уравнения на плотность получим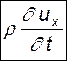
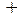


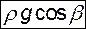

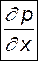
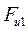
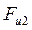
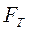
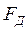
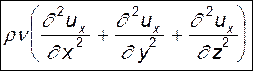
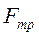
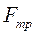 - сила вязкого трения.
- сила вязкого трения.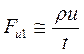 ;
; 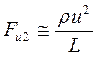 ;
; 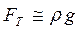 ;
;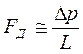 ;
; 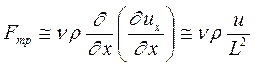
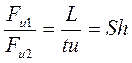 - это так называемый критерий гомохронности либо число подобия Струхаля.
- это так называемый критерий гомохронности либо число подобия Струхаля.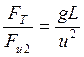 , обратная величина
, обратная величина 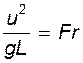 - число Фруда - отношение сил инерции к силам тяжести.
- число Фруда - отношение сил инерции к силам тяжести.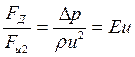 - число Эйлера, отношение сил давления к силам инерции.
- число Эйлера, отношение сил давления к силам инерции.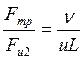 , обратная величина
, обратная величина  - уже известное нам число Рейнольдса - отношение сил инерции к силам вязкого трения.
- уже известное нам число Рейнольдса - отношение сил инерции к силам вязкого трения.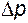 - перепад давления (потеря давления), которая, как правило, является искомой. Другими словами, величина числа Эйлера является следствием (результатом) процесса. Числа подобия такого рода называются неопределяющими. С чисто математических позиций сказанное можно представить в виде
- перепад давления (потеря давления), которая, как правило, является искомой. Другими словами, величина числа Эйлера является следствием (результатом) процесса. Числа подобия такого рода называются неопределяющими. С чисто математических позиций сказанное можно представить в виде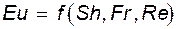 (13.7)
(13.7)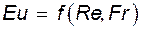 (13.8)
(13.8)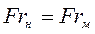 ;
; 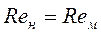
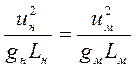 ;
; 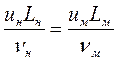 (13.9)
(13.9)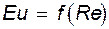 и
и 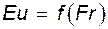 (13.10)
(13.10)