
|
|
Основные выводы и результаты· Сети Петри это инструмент для математического моделирования и исследования сложных систем. Они предназначены для моделирования систем, которые состоят из множества взаимодействующих друг с другом компонент. · Используются два способа моделирования систем сетью Петри: строится система и моделируется сетью Петри; строится оптимальная модель системы в виде сети Петри, на основе которой разрабатывается система. · Представление системы сетью Петри основано на понятиях событие и условие. Возникновением событий управляет состояние системы, которое может быть описано множеством условий. · В сетях Петри отсутствует измерение времени. В них учитывается лишь важнейшее свойство времени – частичное упорядочение событий. · Сети Петри удачно представляют структуру и управление программ. Они предназначены для моделирования упорядочения действий и потока информации, а не для вычисления значений. · Cети Петри используют для моделирования параллельных систем взаимодействующих процессов. Они могут моделировать различные механизмы синхронизации процессов. · Качество моделирования систем сетями Петри обусловлено возможностью исследования их поведения на основе анализа свойств моделирующей сети Петри. · Существуют методы автоматического анализа свойств сетей Петри. · Теорема. Дерево достижимости сети Петри конечно. · На основе дерева достижимости осуществляется анализ свойств сетей Петри: анализ безопасности и ограниченности, сохранения, покрываемости, живости. К сожалению, в общем случае его нельзя использовать для решения задач достижимости и активности, эквивалентности.
Контрольные вопросы и задания 1. Постройте граф сети Петри для следующей структуры сети Петри:P = {p1, p2, p3, p4}, T = {t1, t2, t3, t4}, I(t1) = {}, I(t2) = {p1}, I(t3) = {p2, p4}, I(t4) = {}, I(t5) = {p3}, O(t1) = {p1}, O(t2) = {p2}, O(t3) = {p1, p3},O(t4) = {p3}, O(t5) = {p4}. 2. Изобразите граф сети Петри следующей структуры: P = {p1 p2}, T = {t1, t2, t3}, I(t1) = {p1}, I(t2) = {p1}, I(t3) = {p2}, O(t1) = {p1, p2},O(t2) = {p2}, O(t3) = {}. 3. Какое значение для сети Петри имеет маркировка? 4. Для структуры сети Петри: С = (P, T, I, O), P = {p1, p2, p3, p4, p5}, T = {t1, t2, t3, t4}, I(p1) = {}, I(p2) = {t1, t4}, I(p3) = {t1, t4}, I(p4) = {t3},I(p5) = {t1, t2}, O(p1) = {t1}, O(p2) = {t2}, O(p3) = {t2, t3}, O(p4) = {t4}, O(p5) = {t2}, I(t1) = {p1}, I(t2) = {p2, p3, p5}, I(t3) = {p3}, I(t4) = {p4}, O(t1) = {p2, p3, p5}, O(t2) = {p5}, O(t3) = {p4}, O(t4) = {p2, p3} изобразите граф сети Петри и укажите на графе маркировку m = <1, 0, 1, 1, 0, 0>. 5. Сеть Петри задания 3 имеет маркировку m = <1, 2, 0, 0, 1>. Какие переходы в ней разрешены? 6. Сеть Петри задания 3 имеет маркировку m = <1, 2, 0, 0, 1>. Какая маркировка получится при запуске перехода t1? 7. Охарактеризуйте класс сетей Петри, для которых последовательность маркировок не определяет единственную последовательность запусков. 8. Покажите, что "m 9. Докажите, что если m’ 10. Докажите, что m’ 11. Разработайте теорию сетей Петри, разрешающую существование окрашенных фишек. Рассмотрите различия в определениях разрешенных переходов и запусков переходов. 12. Промоделируйте вычислительную систему с тремя процессами и четырьмя ресурсами: стример (устройство ввода с магнитной ленты), печатающее устройство, диск и два раздела памяти. Любой процесс может попасть в любой раздел. Использование ресурсов тремя процессами состоит в следующем: а) процесс 1 запрашивает стример и печатающее устройство, а затем освобождает оба эти ресурса; б) процесс 2 запрашивает стример и диск, а затем освобождает стример, запрашивает печатающее устройство и в конце концов, освобождает и печатающее устройство, и диск; в) процесс 3 требует все три ресурса одновременно, и затем их освобождает. 13. Напишите программу, осуществляющую построение дерева достижимости по описанию сети Петри и начальной маркировке. 14. Постройте деревья достижимости для маркированной сети Петри, представленной заданием 4. 15. Какова цель анализа сети Петри? Какие вопросы о сети Петри можно задать?

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
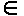 Nn,
Nn, 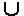 R(C, m) = Nn.
R(C, m) = Nn.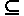 R(C, m).
R(C, m).