
|
|
Логико-термальная эквивалентность
Отношение эквивалентности Е, заданное на парах стандартных схем, называют корректным, если для любой пары схем S1 и S2 из S1 ~Е~ S2 следует, что S1~ S2, т. е. S1 и S2 функционально эквивалентны. Поиск разрешимых корректных отношений эквивалентности представляет значительный интерес с точки зрения практической оптимизации преобразования программ, поскольку в общем виде функциональная эквивалентность стандартных схем алгоритмически неразрешима. Идея построения таких (корректных и разрешимых) отношений связанна с введением понятия истории цепочки схем. В истории с той или иной степенью детальности фиксируются промежуточные результаты выполнения операторов рассматриваемой цепочки. Эквивалентными объявляются схемы, у которых совпадают множества историй всех конечных цепочек. Одним из отношений эквивалентности является логико-термальная эквивалентность (ЛТЭ). Определим термальное значение переменной х для конечного пути w схемы S как терм t(w, x), который строится следующим образом. 1.Если путь w содержит только один оператор А, то: t(w, x) = t, если А – оператор присваивания, t(w, x) = х, в остальных случаях. 2.Если w = w’Ае, где А – оператор, е – выходящая из него дуга, w’ – непустой путь, ведущий к А, а x1, …, xn – все переменные терма t(Ае, x), то t(w, x) = t(Ае, x)[t(w’, x1)/x1, …, t(w’, xn)/xn]. Понятие термального значения распространим на произвольные термы t: t(w, x) = t [t(w, x1)/x1, …, t(w, xn)/xn]. Например, путиstart(х); y:=x; p1(x); x:=f(x); p0(y); y:=x; p1(x); x:=f(x) в схеме на рисунке 1.5, а соответствует термальное значение f(f(x)) переменной х. Для пути w в стандартной схеме S определим ее логико-термальную историю (ЛТИ) lt(S, w) как слово, которое строится следующим образом. 1.Если путь w не содержит распознавателей и заключительной вершины, то lt(S, w) – пустое слово. 2.Если w = w’vе, где v – распознаватель с тестом p(t1, ..., tk), а е – выходящая из него Δ-дуга, Δ lt(S, w) = lt(S, w’) pΔ(t(w’, t1), …, t(w’, tk)). 3.Если w = w’v, где v – заключительная вершина с оператором stop(t1, ..., tk), то lt(S, w) = lt(S, w’) t(w’, t1) … t(w’, tk). Например, логико-термальной историей пути, упомянутого в приведенном выше примере, будет p1(x) p0(x) p1(f(x)). Детерминантом (обозначение: det(S)) стандартной схемы S называют множество ЛТИ всех ее цепочек, завершающихся заключительным оператором. Схемы S1 и S2 называют ЛТЭ (лт - эквивалентными) S1 ~ЛТ~ S2, если их детерминанты совпадают.
Логико-терминальная эквивалентность корректна, т. е. из ЛТЭ следует функциональная эквивалентность (S1 ~ЛТ~ S2 ЛТ – эквивалентность допускает меньше сохраняющих ее преобразований, чем функциональная эквивалентность.
Моделирование стандартных схем программ Одноленточные автоматы Конечный одноленточный (детерминированный, односторонний) автомат обнаруживают ряд полезных качеств, используемых в теории схем программ для установления разрешимости свойств ССП. Одноленточный конечный автомат (ОКА) над алфавитом V задается набором: A = {V, Q, R, q0, #, I} и правилом функционирования, общим для всех таких автоматов. В наборе А: V - алфавит; Q - конечное непустое множество состояний (Q R - множество выделенных заключительных состояний (R q0 - выделенное начальное состояние; I - программа автомата; # - «пустой» символ.
Неформально ОКА можно представить как абстрактную машину, похожую на машину Тьюринга, но имеющую следующие особенности: 1) выделены заключительные состояния; 2) машина считывает символы с ленты, ничего не записывая на нее; 3) на каждом шаге головка автомата, считав символ с ленты и перейдя согласно программе в новое состояние, обязательно передвигается вправо на одну клетку; 4) автомат останавливается в том и только в том случае, когда головка достигнет конца слова, т.е. символа #. Говорят, что автомат допускает слово a в алфавите V, если, начав работать с лентой, содержащей это слово, он останавливается в заключительном состоянии. Автомат A задает характеристическую функцию множества MA допускаемых им слов в алфавите V, т. е. он распознает, принадлежит ли заданное слово множеству MA если связать с остановкой в заключительном состоянии символ 1, а с остановкой в незаключительном состоянии – 0. Наглядным способом задания ОКА служат графы автоматов. Автомат А представляется графом, множество вершин которого – множество состояний Q, и из вершины q в вершину q’ ведет дуга, помеченная символом а, тогда и только тогда, когда программа автомата содержит командуqа Пример 1.2. ОКА A = ({a, b}, {q0, q1, q2, q3}, {q2}, q0, #, I), допускающего слова {an bm | n = 1,2, ...; m = 1,2, ...}, задается графом (рисунок 1.6.). Программа I содержит команды: q0a Автомат называется пустым, если МА = Æ, Автоматы А1 и А2 эквивалентны, если МА1 = МА2. Для машины Тьюринга проблемы пустоты и эквивалентности неразрешимы, более того, они не являются частично разрешимыми. Ситуация меняется для конечных автоматов. Для ОКА доказано: 1) Проблема пустоты ОКА разрешима. Доказательство основано на проверке допустимости конечного множества всех слов, длина которых не превышает числа состояний ОКА - n. Если ни одно слово из этого множества не допускается, то ОКА «пуст». 2) Предположение о том, что минимальная длина допускаемого слова больше n отвергается на том основании, что оно может быть сведено к слову меньшей длины, путем выбрасывания участков между двумя повторяющимися в пути узлами. 3) Проблема эквивалентности ОКА разрешима. Доказательство основано на использовании отношения эквивалентности двух состояний q и q': если состояния q и q' эквивалентны, то для всех a Многоленточные автоматы
Многоленточный (детерминированный, односторонний) конечный автомат (МКА) задается так же, как ОКА. Отличие состоит в том, что множество состояний Q разбивается на n ³ 2 подмножеств (непересекающихся) Q1, ..., Qn. «Физическая» интерпретация n - ленточного автомата отличается тем, что он имеет n лент и n головок, по головке на ленту. Если автомат находится в состоянии q Рассмотрим функционирование МКА с n = 2 (рисунок 1.7.) на примере сравнения пар слов в алфавите {1, 0} и допуске только совпадающих слов. Здесь Q = Q1 В том случае, когда слова совпадают, МКА остановится в заключительном состоянии q01 (именно в этом состоянии поступит символ #) и набор будет допущен. Если слова не совпадут хотя бы в одном символе, МКА перейдет в состояние q32, из которого не выйдет до появления символа #, который и зафиксирует отсутствие совпадения слов, т.е. не допустит искаженный набор. Доказана разрешимость проблемы эквивалентности двухленточных автоматов. Двухголовочные автоматы
Более того, в последнем случае она не является даже частично разрешимой. Проблема эквивалентности также не является частично разрешимой для многоголовочных автоматов. Однако проблема эквивалентности разрешима для двухленточных автоматов, и остается пока открытой для многоленточных автоматов с тремя и более лентами. Двухголовочный конечный автомат (ДКА) имеет одну ленту и две головки, которые могут независимо перемещаться вдоль ленты в одном направлении. Множество состояний Q разбито на два непересекающихся множества. В состояниях Q1 активна первая головка, а в состояниях Q2 - вторая. Двухголовочный автомат можно рассматривать как такой двухленточный автомат, который работает с идентичными словами на обеих лентах. Приведем пример ДКА, который проверяет равенство двух последовательно записанных слов в алфавите V = {0, 1}. Признаком окончания каждого из слов сделаем вспомогательный символ *, не входящий в V. Автомат должен допускать только слова вида а*, а Находясь в состоянии g01, автомат передвигает первую головку к началу второго слова и, обнаружив его, переходит в состояние q11. Если конец ленты # встречается раньше символа *, автомат переходит в незаключительное состояние q62. Если же автомат приходит к состоянию q11, он считывает поочередно символы второго слова первой головкой (состояние q11), а символы первого слова — второй головкой (состояния q32 и q52), сравнивая эти символы. Автомат возвращается каждый раз в состояние q11, если символы одинаковы. Если же обнаружится несовпадение символов или первая головка встречает конец слова раньше символа *, автомат уходит в состояние q62. Попав в это состояние, автомат не может выйти из него; перемещая вторую головку к концу слова на ленте, он достигает #, находясь в незаключительном состоянии, так что слово на ленте отвергается. Если первая головка достигнет конца второго слова, а вторая головка обнаружит, что первое слово тоже просмотрено до конца, то автомат перейдет в заключительное состояние q71. В противном случае автомат перейдет в состояние q62, отвергая слово. Этот пример легко обобщить на случай произвольного алфавита V, увеличивая количество состояний множества Q. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
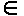 {0,1}, то
{0,1}, то Приведем без доказательства следующие утверждение:
Приведем без доказательства следующие утверждение: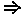 S1 ~ S2). Обратное утверждение как видно из рисунка 1.5 не верно.
S1 ~ S2). Обратное утверждение как видно из рисунка 1.5 не верно. V=Æ);
V=Æ);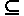 Q);
Q); Программа автомата I представляет собой множество команд вида qа
Программа автомата I представляет собой множество команд вида qа 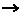 q', в которой q,q'
q', в которой q,q' 
 j) i-я головка останавливается, а j-я начинает читать свою ленту. МКА останавливается, когда головка на одной из лент прочитает символ #.
j) i-я головка останавливается, а j-я начинает читать свою ленту. МКА останавливается, когда головка на одной из лент прочитает символ #. Q2, где Q1={q01}; Q2={q12, q22, q32}; R={q01}; V={0, 1}, начальное состояние - q01. МКА обрабатывает наборы слов (U1, U2), где слово U1 записано на первой ленте, а U2 - на второй. Допустимое множество наборов MA -это все возможные пары одинаковых слов, т.е. наборы, где U1 = U2. Например, набор может быть (1101, 1101) и т.п.
Q2, где Q1={q01}; Q2={q12, q22, q32}; R={q01}; V={0, 1}, начальное состояние - q01. МКА обрабатывает наборы слов (U1, U2), где слово U1 записано на первой ленте, а U2 - на второй. Допустимое множество наборов MA -это все возможные пары одинаковых слов, т.е. наборы, где U1 = U2. Например, набор может быть (1101, 1101) и т.п. Несмотря на то, что двухленточные и двухголовочные автоматы похожи друг на друга, их свойства сильно отличаются. Так, проблема пустоты разрешима для многоленточных автоматов и неразрешима для многоголовочных.
Несмотря на то, что двухленточные и двухголовочные автоматы похожи друг на друга, их свойства сильно отличаются. Так, проблема пустоты разрешима для многоленточных автоматов и неразрешима для многоголовочных.