
|
|
Задача об обедающих философах.Напомним, что задача об обедающих философах была предложена Дейкстрой и связана с пятью философами, которые попеременно то гуляли по саду и думали, то ели. За едой философы сидят за круглым столом, в центре которого стояла большая миска спагетти. На столе также лежало пять вилок, по одной между соседними посадочными местами. Для употребления спагетти необходимо две вилки. Поэтому каждый философ должен сначала взять вилку слева и вилку справа, а затем приступать к еде. Возможна ситуация, в которой каждый философ возьмет вилку слева, а затем будет ждать, когда освободится вилка с правой стороны. Так они будут ждать, пока не умрут от голода. Тем самым, это состояние системы «обедающие философы» является тупиковым.
В этой сети Петри позиция пi, i Каждому философу i
Анализ сетей Петри
Моделирование систем сетями Петри, прежде всего, обусловлено необходимостью проведения глубокого исследования их поведения. Для проведения такого исследования необходимы методы анализа свойств самих сетей Петри. Этот подход предполагает сведение исследования свойств реальной системы к анализу определенных свойств моделирующей сети Петри. Свойства сетей Петри
Позиция p Позиция p Сеть Петри N = (P,Т,I,O) с начальной маркировкой m является сохраняющей, если для любой достижимой маркировки m’
Тупик в сети Петри – один или множество переходов, которые не могут быть запущены. Определим для сети Петри N с начальной маркировкойm следующие уровни активности переходов: Уровень 0: Переход t обладает активностью уровня 0 и называется мёртвым, если он никогда не может быть запущен. Уровень 1: Переход t обладает активностью уровня 1 и называется потенциально живым, если существует такаяm’ Уровень 2: Переход t, обладает активностью уровня 2 и называется живым, если для всякой m’ Сеть Петри называется живой, если все её переходы являются живыми. Задача достижимости: Для данной сети Петри с маркировкойm и маркировки m’ определить: m’ Задача покрываемости:Для данной сети Петри N с начальной маркировкой m и маркировки m’ определить, существует ли такая достижимая маркировка m” (Отношение m" ³ m’ истинно, если каждый элемент маркировки m" не меньше соответствующего элемента маркировки m’.) Сети Петри присуще некоторое поведение, которое определяется множеством ее возможных последовательностей запусков переходов или ее множеством достижимых маркировок. Понятие эквивалентности сетей Петри определяется через равенство множеств достижимых маркировок. Сеть Петри N = (P,Т,I,O) с начальной маркировкой m и сеть Петри N’ = (P’,Т’,I’,O’) с начальной маркировкой m’ эквивалентны, если справедливо R(N,m) = R(N’,m’). Понятие эквивалентности сетей Петри может быть определено также через равенство множеств возможных последовательностей запусков переходов. Более слабым, по сравнению с эквивалентностью, является свойство включения, определение которого совпадает с определением эквивалентности, с точностью до замены = на
Методы анализа
Особый интерес вызывают методы анализа свойств сетей Петри, которые обеспечивают автоматический анализ моделируемых систем. Сначала рассмотрим метод анализа сетей Петри, который основан на использовании дерева достижимости. Дерево достижимости
Пример 4.4.Частичное дерево достижимости маркированной сети Петри изображено на рисунке 4.11, а, а частичное дерево достижимости для трёх шагов построения имеет вид (рис. 4.11, б). Для сети Петри с бесконечным множеством достижимых маркировок дерево достижимости является бесконечным. Сеть Петри с конечным множеством достижимых маркировок также может иметь бесконечное дерево достижимости (см. пример 4.4). Для превращения бесконечного дерева в полезный инструмент анализа строится его конечное представление. При построении конечного дерева достижимости для обозначения бесконечного множества значений маркировки позиции используется символ w. Также используются следующие ниже операции надw,определяемые для любого постоянного a. w -- а = w; w + а = w; а < w; w Алгоритм построения конечного дерева достижимости. Каждая вершина дерева достижимости классифицируется алгоритмом или какграничная вершина, терминальная вершина, дублирующая вершина, или как внутренняя вершина. Алгоритм начинает работу с определения начальной маркировки корнем дерева, и граничной вершиной. Один шаг алгоритма состоит в обработке граничной вершины. Пусть х — граничная вершина, тогда её обработка заключается в следующем: 1. Если в дереве имеется другая вершина y, не являющаяся граничной, и с ней связана та же маркировка, m[x]=m[y], то вершина х становится дублирующей. 2. Если для маркировки m[х] ни один из переходов не разрешен, то x становится терминальной. 3. В противном случае, для всякого перехода t 3.1. Если m[х](p) = w, то m[z](p) = w. 3.2. Если на пути от корневой вершины к x существует вершина y с m[y] < m’ (где m’ – маркировка, непосредственно достижимая из m[х] посредством запуска перехода t) и m[y](p) < m’(p), то m[z](p) = w. (В этом случае последовательность запусков переходов, ведущая из маркировки m[y] в маркировку m’, может неограниченно повторяться и неограниченно увеличивать значение маркировки в позиции p.) В противном случае m[z](p) = m’(p). 4. Строится дуга с пометкой t, направленная от вершины x к вершине z. Вершина х становится внутренней, а вершина z – граничной. Такая обработка алгоритмом граничных вершин продолжается до тех пор, пока все вершины дерева не станут терминальными, дублирующими или внутренними. Затем алгоритм останавливается. Важнейшим свойством алгоритма построения конечного дерева достижимости является то, что он за конечное число шагов заканчивает работу.
Сеть Петри и ее конечное дерево достижимости изображены на рис. 4. 12.: Важнейшим свойством алгоритма построения конечного дерева достижимости является то, что он за конечное число шагов заканчивает работу. Доказательство основано на трёх леммах. Лемма 4.1. В любом бесконечном направленном дереве, в котором каждая вершина имеет только конечное число непосредственно последующих вершин, существует бесконечный путь, исходящий из корня. Доказательство. Пусть x0 корневая вершина. Поскольку имеется только конечное число непосредственно следующих за x0 вершин, но общее число вершин в дереве бесконечно, по крайней мере, одна из непосредственно следующих за x0 вершин должна быть корнем бесконечного поддерева. Выберем вершину x1 непосредственно следующую за x0 и являющуюся корнем бесконечного поддерева. Теперь одна из непосредственно следующих за ней вершин также является корнем бесконечного поддерева, выберем в качестве такой вершины x2. Если продолжать этот процесс бесконечно, то получим бесконечный путь в дереве – x0,x1,x2,…,xn,… . Лемма 4.2. Всякая бесконечная последовательность неотрицательных целых содержит бесконечную неубывающую последовательность. Доказательство. Возможны два случая: 1. Если какой-либо элемент последовательности встречается бесконечно часто, то пусть x0 является таким элементом. Тогда бесконечная подпоследовательность x0,x0,…,x0,… является бесконечной неубывающей подпоследовательностью. 2. Если никакой элемент не встречается бесконечно часто, тогда каждый элемент встречается только конечное число раз. Пусть x0 —произвольный элемент последовательности. Существует самое большее x0 целых, неотрицательных и меньших, чем x0 (0,..., x0 - 1), причем каждый из них присутствует в последовательности только конечное число раз. Следовательно, продвигаясь достаточно долго по последовательности, мы должны встретить элемент x1, x1 ³ x0. Аналогично должен существовать в последовательности x2, x2 ³ x1, и т. д. Это определяет бесконечную неубывающую последовательность x0,x1,x2,…,xn,… . Таким образом, в обоих случаях бесконечная неубывающая подпоследовательность существует. Лемма 4.3. Всякая бесконечная последовательность n-векторов над расширенными символом w неотрицательными целыми содержит бесконечную неубывающую подпоследовательность. Доказательство.Доказываем индукцией по n, где n — размерность векторного пространства. 1. Базовый случай (n = 1). Если в последовательности имеется бесконечное число векторов вида <w>, то они образуют бесконечнуюнеубывающую последовательность (так как справедливо w 2. Индуктивное предположение. (Допустим, что лемма верна для n докажем её справедливость для n+1.) Рассмотрим первую координату. Если существует бесконечно много векторов, имеющих. в качестве первой координаты w, тогда выберем эту бесконечную подпоследовательность, которая не убывает (постоянна) по первой координате. Если только конечное число векторов имеют w в качестве первой координаты, то рассмотрим бесконечную последовательность целых, являющихся значениями первых координат. По лемме 4.2 эта последовательность имеет бесконечную неубывающую подпоследовательность. Она определяет бесконечную последовательность векторов, которые не убывают по своей первой координате. В любом случае мы имеем последовательность векторов, неубывающих по первой координате. Применим индуктивное предположение к последовательности n-векторов, которая получается в результате отбрасывания первой компоненты n+1-векторов. Полученная бесконечная подпоследовательность является неубывающей по каждой координате. Докажем следующую теорему. Теорема 4.1. Дерево достижимости сети Петри конечно. Доказательство. Докажем методом от противного. Допустим, что дерево достижимости бесконечно. Тогда по лемме 4.1 (и так как число вершин, следующих за каждой вершиной в дереве, ограничено числом переходов m) в нём имеется бесконечный путь x0,x1,x2,… , исходящий из корня x0. Тогда m[x0], m[x1], m[x2],… — бесконечная последовательность n-векторов. над Nat 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Проблема тупика в этой системе может быть решена путем следующей модификации ее правил поведения. Пусть философ при переходе из состояния размышления в состояние приема пищи берет одновременно обе вилки (слева и справа), если они свободны. Сеть Петри (рис. 4.10) моделирует такую модифицированную систему обедающих философов, свободную от тупиков.
Проблема тупика в этой системе может быть решена путем следующей модификации ее правил поведения. Пусть философ при переходе из состояния размышления в состояние приема пищи берет одновременно обе вилки (слева и справа), если они свободны. Сеть Петри (рис. 4.10) моделирует такую модифицированную систему обедающих философов, свободную от тупиков.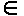 {1,2,3,4,5}, представляет условие «i-тая вилка свободна». В начальной маркировке каждая из этих позиций имеет фишку. Каждому философу i
{1,2,3,4,5}, представляет условие «i-тая вилка свободна». В начальной маркировке каждая из этих позиций имеет фишку. Каждому философу i 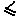 k для любой достижимой маркировки m’
k для любой достижимой маркировки m’  .
.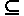 .
. Дерево достижимости представляет все достижимые маркировки сети Петри, а также – все возможные последовательности запусков ее переходов.
Дерево достижимости представляет все достижимые маркировки сети Петри, а также – все возможные последовательности запусков ее переходов. Пример 4.5.Конечное дерево достижимости сети Петри.
Пример 4.5.Конечное дерево достижимости сети Петри.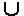 {w}, а по лемме 4.3 она имеет бесконечную неубывающую подпоследовательность m[xk0]
{w}, а по лемме 4.3 она имеет бесконечную неубывающую подпоследовательность m[xk0]  m[xj] (для i
m[xj] (для i