
|
|
Соответствие спецификацииЕсли Р - объект, отвечающий спецификацииS, то говорят, что Р удовлетворяет S, сокращенно Р уд S. Это означает, что S описывает все возможные результаты наблюдения за поведением Р, или, другими словами, S истинно всякий раз, когда его переменные принимают значения, полученные в результате наблюдения за объектом Р, или, более формально: "пр.пр В следующих законах приводятся наиболее общие свойства отношения удовлетворяет. Спецификации истина, не накладывающей никаких ограничений на поведение, будут удовлетворять все объекты. L1.P уд истина. Если объект удовлетворяет двум различным спецификациям, он удовлетворяет также и их конъюнкции: L2А.Если Р уд S и Р уд Т, то Р уд (S AND T). Пусть S(n) — предикат, содержащий переменную n и Р не зависит от n. L2B.Если "n.(Р уд S(n)), то Р уд "n.S(n). Если из спецификации S логически следует другая спецификация T, то всякое наблюдение, описываемое S, описывается также и Т. LЗ.Если Р уд S и S Доказательства При проектировании изделия разработчик несёт ответственность за то, чтобы оно соответствовало своей спецификации. Эта ответственность может быть реализована посредством обращения к методам соответствующих разделов математики. В этом разделе мы приводим набор законов, позволяющих с помощью математических рассуждений убедиться в том, что процесс Р соответствует своей спецификации S. Результатом наблюдения за процессом СТОП всегда будет пустой протокол: L4А.СТОП уд (пр = <>). Протокол процесса (с L4В.Если Р уд S(пр), то (с Все приведенные выше законы являются частными случаями закона для обобщенного оператора выбора: L5.Если "x (х: В Закон, устанавливающий корректность рекурсивно определенного процесса. L6.Если F(X) — предваренная, СТОП уд S, а ((X уд S) (mХ.F(Х)) уд S. Пример 1.16. Докажем, что ТАП уд ТАПВЗАИМ. Доказательство. 1) СТОП уд(пр = <>) (<> ¯ мон) = (<> ¯ шок) = 0. Это заключение сделано на основании применения законов L4A и LЗ. 2) Предположим, что Х уд (0 (мон AND (0
так как <> ¯ мон = <> ¯ шок = <мон> ¯ шок = 0, а <мон> ¯ мон = = <мон, шок> ¯ мон = <мон, шок> ¯ шок = 1 и пр ³ <мон ,шок>
Применяя теперь закон L3, а затем — L6, получим требуемый результат. Тот факт, что процесс Р удовлетворяет спецификации, еще не означает, что он будет нормально функционировать. Например, так как пр = <> то с помощью законов L3, L4 можно доказать, что СТОП уд0 Однако СТОП не соответствует ни требованиям владельца торгового автомата, ни покупателя. Он не сделает ничего плохого, но только потому, что он не делает ничего вообще. По той же причине СТОП удовлетворяет любой спецификации, которой может удовлетворять процесс. Параллельные процессы Процесс определяется полным описанием его потенциального поведения. При этом часто имеется выбор между несколькими различными действиями. В каждом таком случае выбор того, какое из событий произойдет в действительности, может зависеть от окружения, в котором работает процесс. Само окружение процесса может быть описано как процесс, поведение которого определяется в уже знакомых терминах. Это позволяет исследовать поведение целой системы, состоящей из процесса и его окружения, взаимодействующих по мере их параллельного исполнения. Всю систему также следует рассматривать как процесс, поведение которого определяется в терминах поведения составляющих его процессов. Эта система в свою очередь может быть помещена в еще более широкое окружение, и т.д.
Взаимодействие
Объединяя два процесса для совместного исполнения, как правило, хотят, чтобы они взаимодействовали друг с другом. Эти взаимодействия можно рассматривать, как события, требующие одновременного участия обоих процессов. Законы Законы, управляющие поведением (P || Q), параллельно развивающихся процессов P и Q, достаточно просты. Первый закон выражает логическую симметрию между процессом и его окружением: L1.P || Q = Q || P. Следующий закон показывает, что при совместной работе трех процессов неважно, в каком порядке они объединены оператором параллельной композиции ||: L2.P || (Q || R) = (P || Q) || R. Процесс, находящийся в тупиковой ситуации, приводит к тупику всей системы. L3.P || СТОПaP = СТОПaP. Следующий закон гласит, что пара процессов с одинаковыми алфавитами либо одновременно выполняет одно и то же действие, либо попадает в состояние тупика, если начальные события процессов не совпадают: L4А. (с L4B. (с
Параллелизм
Рассмотрим случай, когда операнды Р и Q оператора || имеют неодинаковые алфавиты aР Когда такие процессы объединяются для совместного исполнения, события, содержащиеся в обоих алфавитах, требуют одновременного участия Р и Q. События же из алфавита Р, не содержащиеся в алфавите Q, не имеют никакого отношения к Q, который физически неспособен ни контролировать, ни замечать такие события. Такие события процесса P могут происходить независимо от Q. Аналогично Q может самостоятельно участвовать в событиях, содержащихся в его алфавите, но отсутствующих в алфавите Р. Таким образом, множество всех событий, логически возможных для данной системы, есть просто объединение алфавитов составляющих ее процессов a(Р || Q) = aР
Законы Формальное описание вышесказанного осуществляется с помощью следующих законов: Пусть а L1А. (с L1B. (с L2А. (a L2B.(с L3.(a Эти законы можно обобщить для общего случая оператора выбора: L3.Пусть Р = (х: А Р || Q = (z: C где С = (A С помощью этих законов можно переопределить процесс, удалив из его описания, параллельный оператор, как это показано в следующем примере. Пример 3.17. Пусть aР = {a, c}, aQ = {b, c}, P = (a Р || Q = (a = a (P || (b = a = a = mX.(a Отсюда следует, что Р || Q = a Реализация Реализация операции || выводится непосредственно из закона L3. Алфавиты операндов представляются конечными списками символов A и B. Протоколы Пусть t — протокол (Р || Q). Тогда все события из t, принадлежащие алфавиту aР, являлись событиями в жизни P, а все события из t, не принадлежащие aР, происходили без участия P. Таким образом, (taР) — это протокол всех событий, в которых участвовал процесс P, и поэтому он является протоколом P. По тем же соображениям (taQ) является протоколом Q. Более того, каждое событие из t должно содержаться либо вaР, либо в aQ. Эти рассуждения позволяют сформулировать закон L1. протоколы(Р || Q) = {t | (taР) AND (taQ)

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
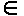 препротоколы(Р)
препротоколы(Р) 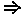 S.
S.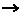 Р) вначале пуст. Каждый последующий протокол начинается с c, а его хвост является протоколом Р.
Р) вначале пуст. Каждый последующий протокол начинается с c, а его хвост является протоколом Р.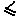 (пр ¯ мон – пр ¯ шок)
(пр ¯ мон – пр ¯ шок)  aQ.
aQ. aQ.
aQ. aQ). Следующие законы показывают, каким образом процесс Р один участвует в событии a, Q один участвует в b, а c и d требуют одновременного участия P и Q.
aQ). Следующие законы показывают, каким образом процесс Р один участвует в событии a, Q один участвует в b, а c и d требуют одновременного участия P и Q.