Трансляция обогащенных схем

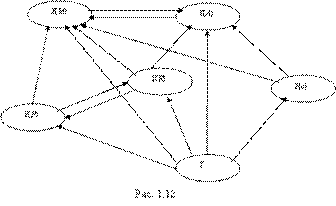
Диаграмма на рис. 1.12. дает полную информацию о возможности трансляции одного класса схем в другой, классы имеют следующие обозначения:

Y — стандартные схемы; Y(М) — магазинные схемы;

Y(R) — рекурсивные схемы; Y(А) — схемы с массивами;

Y(с) — счетчиковые схемы;Y(P) — схемы с процедурами.

Диаграмма показывает, что классы Y(М) и Y(А) являются универсальными в том смысле, что схемы всех других классов транслируемы в них. В то же время, в класс Y не транслируются схемы ни одного другого класса. Следует отметить, что класс Y(с) достигает полной мощности при количестве счетчиков не менее 2, т.е. класс Y(с) с одним счетчиком равномощен классу Y.

О сравнении классов схем

Программы для ЭВМ, будь-то программы, записанные на операторном языке, или программы на рекурсивном языке, универсальны в том смысле, что любую вычислимую функцию можно запрограммировать и найти ее значения для заданных значений аргументов. При этом не требуется богатого набора программных примитивов и базовых операций: достаточно тех средств, которые моделируются стандартными схемами. Это значит, что различные классы программ не имеет смысла сравнивать способности реализовать различные алгоритмы, — все они оказываются универсальными. В то же время программисты знают, чтоодни программные примитивы являются «более выразительными», чем другие, что запись алгоритмов с привлечением рекурсии короче, чем итерационное представление, но вычисления по такой программе могут потребовать больше времени, и т. д. При переходе к схемам программ возникает возможность поставить и исследовать проблему выражения одних наборов примитивов через другие в более чистом виде. Задачи такого типа образуют сравнительную схематологию, основу которой составляют теоремы о возможности или невозможности преобразования схем из одного класса в схемы другого. При этом наряду с основной задачей — выяснением соотношений между различными средствами программирования — решается и другая, внутренняя задача схематологии. Действительно, если мы умеем трансформировать один класс схем в другой, то сможем переносить результаты, полученные для некоторого класса схем, на другие классы.

Мы будем сравнивать классы схем, у которых базисы согласованны в том смысле, что множества переменных, базовых функциональных символов и предикатных символов одинаковы в данных базисах. Это дает возможность превращать в программы схемы из разных классов с помощью одной и той же интерпретации базисов. Например, полные базисы стандартных и рекурсивных схем согласованны, т. е. определение функциональной эквивалентности может быть обобщено на схемы из разных классов.

Схема S₁ из класса W и схема S₂ из класса W’ функционально эквивалентны, если для любой интерпретации I согласованных базисов классов W и W’ программы (S₁, I), (S₂, I)или обе зацикливаются, или обе останавливаются с одним и тем же результатом.

Класс схем W мощнее класса схем W’, или класс W’ транслируем в класс W, если для любой схемы из W’ существует эквивалентная ей схема в классе W. Классы W и W’ равномощны, если W’ мощнее W и W мощнее W’.

Доказано, что класс ССП транслируем в класс РС и класс РС не транслируем в класс ССП.

Рассмотренные примеры подтверждают первое утверждение для одинаковых интерпретаций I базисов. В этом случае РС R_S1 эквивалентна ССП S₁. При разных интерпретациях ССП и РС результаты будут различаться и следовательно программы (R_S1, I₁) и (S₁, I₂) будут различны.

Второе утверждение подкрепляется РС R_S3. Причина не транслируемости этой схемы обусловлена тем, что при варьировании интерпретаций возникает необходимость запомнить сколь угодно большое число промежуточных значений, в то время как память любой стандартной схемы ограничена.

Существуют некоторые классы РС, транслируемые в ССП. К ним относится класс линейных унарных РС, имеющих базис с единственной переменной x и одноместными функциональными и предикатными символами. Например:

R_S4: F(x); F(x)=ifp(x) then x elsef(x, F(g(x))) транслируема в ССП.

Схемы с процедурами

Схемы с процедурами строятся в объединенном базисе классов стандартных и рекурсивных схем. Она состоит из двух частей - главной схемы и множества схем процедур. Главная схема - это стандартная схема, в которой имеются операторы присваивания специального вида x := F⁽ⁿ⁾(y₁,y₂,…y_n), называемые операторами вызова процедур. Схема процедуры состоит из заголовка и телапроцедуры, разделенных символом равенства. Заголовок имеет тот же вид, что и левая часть рекурсивных уравнений. Тело процедуры - это стандартная схема того же вида, что и главная схема. Заключительный оператор тела процедуры всегда одноместен (stop(х)). Ниже приведен пример схемы с процедурами.

Доказано, что класс РС транслируем в класс схем с процедурами и наоборот.

Обогащенные и структурированные схемы

Классы обогащенных схем

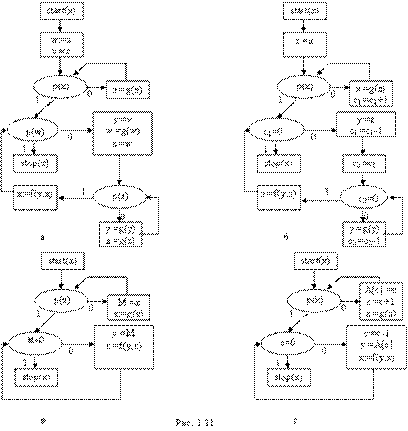
Выделяют следующие классы обогащенных схем: класс счетчиковых схем, класс магазинных схем, класс схем с массивами.

Классы счетчиковых имагазинных схем образован добавлением в базис ССП счетного множества счетчиков и магазинов с их интерпретированными операторами.

Счетчик — интерпретированная переменная, у которой областью значений является множество Nat; начальное значение счетчика равно 0.

Интерпретированные операторы имеют следующий вид:

c := c + 1 — оператор прибавления единицы;

c := c - 1— оператор вычитания единицы;

c = 0 — условный оператор проверки равенства счетчика нулю.

При значении счетчика равном 0 оператор вычитания единицы не изменяет его, оно остается равным 0.

К интерпретированным операторам может быть добавлен оператор пересылки значения счетчика с₂ := с₁, который может быть получен при помощи стандартных операторов.

Магазин — неинтерпретированная переменная сложной структуры. В процессе выполнения интерпретированной схемы состояние магазина — это конечный набор элементов (d₁,d₂,…,d_n) из области интерпретации, где d_n — верхушка магазина.

Интерпретированные операторы имеют следующий вид:

М := x — запись в магазин;

х := М — выборка из магазина;

М = Æ — условный оператор проверки пустоты магазина,

где М – магазин, х - обычная переменная. Первый оператор меняет состояние (d₁,d₂,…,d_n) магазина М на состояние (d₁,d₂,…,d_n+1), где d_n+1 - значение переменной х. После выполнения этого оператора элемент d_n+1 становится новой верхушкой магазина. Второй оператор присваивает переменной х значение, равное верхушке магазина, состояние которого меняется с (d₁,d₂,…,d_n-1,d_n) на (d₁,d₂,…,d_n-1), при этом d_n-1 становится новой верхушкой магазина. Если магазин М пуст, то применение второго оператора оставляет его пустым, а переменная х не меняет своего значения. Третий оператор - предикат проверки магазина на пустоту; если магазин пуст, то значение предиката М = 0 равно 1, в противном случае - 0.

Класс схем с массивами — это расширение класса счетчиковых схем за счет добавления счетного множества массивов и операторов над ними.

Массив — неинтерпретированная переменная сложной структуры. При выполнении интерпретированной схемы состояние массива — бесконечная последовательность (d₁,d₂,…,d_i,…) элементов из области интерпретациии.

Интерпретированные операторы имеют следующий вид:

А[c]:= x — запись в массив;

х:= А[c] — выборка из массива,

где А — массив, [c] — целое число, равное текущему значению счетчика с.

На рисунке 1.11 приведены четыре схемы: стандартная (а), счетчиковая (б), магазинная (в) и схема с массивами (г). Все они эквивалентны друг другу и рекурсивной схеме:

F(x), F(x)=ifp(x) thenx else f(x, F(g(x))).

Не нашли, что искали? Воспользуйтесь поиском по сайту: