|
|
Доказательство беступиковостиДокажем утверждение, что НОВПАНСИОН свободен от тупиков. Для этого достаточно доказать, что любой протокол s этой системы можно продолжить некоторым событием так, что бы снова получить протокол этой же системы. Строго, это можно сформулировать как "s, $z (s s^z Доказательство можно осуществлять двумя способами: Первый из них предполагает применение (насколько это возможно) приведённых выше законов. Второй способ доказательства состоит в составлении компьютерной программы для исследования протоколов системы в поисках тупика. Такая программ сможет дать интересующий нас ответ за конечное время, если система имеет конечное число состояний, как в нашем случаеНОВПАНСИОН. Достаточно рассмотреть только те протоколы, длина которых не превышает известной верхней границы числа состояний. (Каждому протоколу соответствует некоторое состояние системы, в которое систему приводит из начального состояния последовательность событий, описываемая этим протоколом.) Число состояний в системе НОВПАНСИОН не превышает 1,8 млн. Но, т. к. в каждом состоянии возможны не меньше двух событий, то количество протоколов, которые надо проверить, будет превышать два в степени 1,8 млн. Трудно представить, что компьютер, когда-нибудь сумеет исследовать все возможные случаи. Таким образом, доказательство отсутствия тупиковых ситуаций, как правило, входит в обязанности разработчика параллельных систем. Бесконечный перехват Помимо тупика обедающего философа подстерегает опасность бесконечного перехвата инициативы. Предположим, что левая рука у сидящего философа очень медлительна, в то время как его левый сосед очень проворен. Всякий раз, когда философ пытается дотянуться до своей левой вилки, его левый сосед мгновенно перехватывает ее. Таким образом, может оказаться, что сидящий философ никогда не приступит к еде. При строгом подходе эта проблема неразрешима. Однако, если важно гарантировать, чтобы сидящий философ смог поесть, нужно изменить поведение слуги: проводив философа до его места, он ждет, пока философ не возьмет обе вилки, и только после этого позволяет есть его соседям. Таким образом, добиваться, чтобы любое желаемое и возможное событие обязательно наступило в пределах разумного интервала времени, становится задачей проектировщика системы.
Помеченные процессы
Помечать процессы особенно полезно при создании групп сходных процессов, которые в режиме параллельной работы представляют некоторые идентичные услуги их общему окружению, но никак не взаимодействуют друг с другом. Это означает, что все они должны иметь взаимно непересекающиеся алфавиты. Чтобы этого достичь, снабдим каждый процесс отдельным именем; каждое событие помеченного процесса помечено тем же именем. Помеченное событие l.x, где х – его имя, а l – метка. Процесс P с меткой l обозначают где l: P. Он участвует в событии l.x, когда по определению P участвует в х. Пример 3.18. Два работающих рядом торговых автомата (лев: ТАП) || (прав: ТАП). Алфавиты этих процессов не пресекаются, и каждое происходящее событие помечено именем того устройства, на котором оно происходит. Если перед их параллельной установкой устройства не получили имен, каждое событие будет требовать участия их обоих, и тогда пара машин будет неотличима от одной. Это является следствием того, что (ТАП || ТАП) = ТАП. Пометка позволяет использовать процессы наподобие локальных переменных в языке высокого уровня, описанных в том блоке программы, где они используются.
Множественная пометка
Определение пометки можно расширить, позволив помечать каждое событие любой меткой l из некоторого множества L. Если P – процесс, определим (L: P) как процесс, ведущий себя в точности как P с той разницей, что он участвует в событии l.x (где l Пример 3.19. Лакей – это младший слуга, который имеет одного хозяина, провожает его к столу и из-за стола и прислуживает ему, пока тот ест: aЛАКЕЙ = {садится, встает} ЛАКЕЙ = (садится → встает → ЛАКЕЙ) Лакей обслуживающего всех пятерых философов по очереди определим: L = {0, 1, 2, 3, 4} ОБЩИЙ ЛАКЕЙ = (L: ЛАКЕЙ). Общего лакея можно нанимать на период отпуска слуги для предохранения обедающих философов от тупиковой ситуации. Конечно, в течение этого времени философам придется поголодать, ибо находиться за столом они смогут только по очереди.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
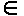 протоколы(НОВПАНСИОН) AND z
протоколы(НОВПАНСИОН) AND z