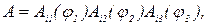|
|
Вращения в трехмерном псевдоевклидовомПространстве индекса два
Линейное преобразование х′=Ахс вещественной матрицей
назовем преобразованием вращения, если его матрица удовлетворяет условию A где черточка обозначает операцию индекс T – операцию транспонирования, G – метрический тензор,
причем a,β=±1, так что G=GT, G2=I и
Очевидно, что и Преобразование вращения в трехмерном псевдоевклидовом векторном пространстве сохраняет квадраты модулей векторов. Такое преобразование является собственным вращением, если оно сохраняет также векторное произведение двух векторов и det ||A||=1. Преобразование с det ||A||= -1 является несобственным вращением или вращением с отражением. Пусть е1, е2, е3 – любой ортонормированный базис, и пусть х=х1е1+х2е2+х3е3 и х′=х1′е1+х2′е2+х3′е3. Каждое преобразование вращения задается формулами х1′= a11 х1+a12 х2 +a13х3, х2′= a21 х1+a22 х2+a23х3, х3′= a31 х1+a32 х2+a33х3 или в матричной форме Х′= AХ, где для собственных вращений det(A)=1. Так как рассматриваемая система координат является ортонормированной, действительная матрица А, описывающая каждое вращение, определяется системой равенств
или, что равносильно,
Любые три из коэффициентов аik определяют все остальные. Геометрически коэффициент аik определяет угол между базисным вектором ei и повернутым базисным вектором ek′=Aek= аik=(ei ek′). Преобразование вращения поворачивает радиус – вектор х каждой точки трехмерного псевдоевклидового пространства на угол поворота δ вокруг направленной оси вращения, точки которой инвариантны. Угол поворота δ, а также направляющие углы положительной оси вращения определяются формулами Chδ= αа23+ а32=2с1Shδ=4λ1λ0, -а31-βа13=2с2Shδ=4λ2λ0, βа12-αа21=2с3Shδ=4λ3λ0. Либо знак угла δ, либо направление оси вращения могут выбираться произвольно. Матрица преобразования А, соответствующая данному вращению, описываемая числами δ, с1, с2,…, с7, есть
Четыре симметричных параметра (Эйлера) λ0 λ02-αλ12-βλ22+αβλ32=1 -αс12-βс22+αβс32= -1 однозначно определяют вращение, так как из выражения для матрицы А следует:
При этом
Будем считать для определенности α=β=1. В принятом предположении Chδ= βа23+ а32=2с1Shδ=4λ1λ0, -а31-βа13=2с2Shδ=4λ2λ0, βа12-βа21=2с3Shδ=4λ3λ0.
Четыре симмметричных параметра (Эйлера) λ02-λ12-βλ22+λ32=1, -βс12-βс22+с32 = -1, однозначно определяют вращение, так как из выражения для матрицы А следует:
при этом
а параметры λ0, λ1, λ2, λ3 и–λ0, –λ1, –λ2, – λ3 представляют одно и то же вращение. Следующие матрицы преобразования описывают правые вращения вокруг положительных координатных осей:
Заметим, что Каждая матрица А, описывающая собственное вращение в трехмерном псевдоевклидовом пространстве, может быть различными способами представлена в виде произведения трех матриц
в частности, так: А=A3(φ1)A2(φ2)A3(φ3)=
Три угла (Эйлера) φ1, φ2, φ3,однозначно определяют вращение; в свою очередь они однозначно определяются данным вращением за исключением случая, когда φ2=0 (карданов подвес). Обратное вращение А-1=
Существуют шесть способов, которыми матрицу вращения можно выразить путем вращения вокруг двух различных осей координат. Кроме того, существует шесть способов представления матриц вращения в виде произведения вращений вокруг трех различных осей координат, в частности, так:
при

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 =
=  =G(AB)TG=G(BTAT)G=(GBTG)(GATG)=
=G(AB)TG=G(BTAT)G=(GBTG)(GATG)= 
 =
= 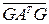 =G(GАТG)TG=GGAGG=A.
=G(GАТG)TG=GGAGG=A. аjkej,
аjkej, (Tr (A)-1)=
(Tr (A)-1)= 
 , λ1
, λ1  , λ2
, λ2  , λ3
, λ3  ,
,

 Аi(-φ), i= 1, 2, 3.
Аi(-φ), i= 1, 2, 3.