|
|
Соотношения неопределенностейПричинная механика Н. А. Козырева [1] начинается с постулатов о том, что в элементарном причинно-следственном звене точка-причина и точка-следствие разделены сколь угодно малыми, но не равными нулю пространственным
Принимается, что константа с2— псевдоскаляр. При этом ее псевдоскалярность связывается с наличием подобного свойства у величины
В причинной механике физический смысл величин
Пусть пространство и время образуют единое четырехмерное многообразие, причем как по пространственным, так и по временной переменным оно обладает собственно евклидовой геометрией (для дальнейшего не имеет значения, какова геометрия всего пространства-времени в целом — собственно евклидова или псевдоевклидова, потому что в настоящем разделе пространственные и временне величины рассматриваются по отдельности). Назовем «столкновением» материальных точек (частиц) их взаимодействие при сближении до минимально возможных пространственного и временного расстояний. Следует отметить, что в различных актах «столкновения» минимальное расстояние между частицами может быть различным, при этом оно заведомо отлично от нуля, так как в евклидовом континууме различающиеся точки всегда разделены ненулевым промежутком. (Мы заключаем термин «столкновение» в кавычки, поскольку «сталкивающиеся» частицы не соприкасаются между собой.) Будем считать, что пространственные и временные координаты «сталкивающихся» материальных точек — независимые случайные переменные, и примем, что величины |
здесь r1, r2, t1, t2 — пространственные радиусы-векторы и временные координаты «столкнувшихся» частиц; черта над символом — процедура усреднения переменной по всем возможным значениям. Предположим, что случайные величины r1 и r2, а также t1 и t2 характеризуются одинаковыми плотностями распределения и одинаковыми средними значениями. Точку пространства-времени, совпадающую со средним положением обеих частиц, назовем точкой столкновения. Именно она воспринимается при макроскопическом описании как место, где находятся обе «столкнувшиеся» частицы. Пространственный радиус-вектор r и временная координата t точки столкновения есть
Среднеквадратические отклонения частиц от точки столкновения в силу тождественности их плотностей распределения одинаковы для обеих частиц и по пространственным и временному направлениям составляют соответственно
Используя формулы (1.3) – (1.5) и независимость случайных величин r1 и r2, можем записать:
где точка – знак скалярного произведения векторов. Отсюда следует, что неопределенность пространственного положения частицы связана с величиной |δx| соотношением
Аналогичным образом для неопределенности временной координаты частицы можно получить следующую связь с |δt|:
При макроскопическом описании «столкновения» в качестве точек приложения сил, действующих на частицы, принимается для обеих частиц одна и та же точка – введенная выше точка столкновения с координатами (1.4). Вместе с тем, действительные пространственные и временные положения частиц и, следовательно, точек приложения сил могут не совпадать с точкой столкновения. Неточность задания точек приложения сил приводит к неточностям в определении энергий и импульсов частиц. При этом неточность значения энергии равна работе, которую произвела бы сила при перемещении частицы от точки столкновения до точки ее истинного местонахождения; а неточность значения импульса равна добавке импульса, которую приобрела бы частица под действием данной силы за промежуток времени, отличающий действительный момент взаимодействия от момента, отвечающего точке столкновения. Таким образом, неточности определения энергии и импульса в каждом отдельном акте «столкновения» для одной частицы равны соответственно F1∙(r1-r) и F1(t1-t), а для другой составляют F2∙(r2-r) и F2(t2-t), где F1, F2 – силы, действующие на первую и вторую частицы. Среднеквадратические значения данных величин могут быть отождествлены с квантовомеханическими неопределенностями энергий и импульсов частиц. Вычислим их. Пусть частицы взаимодействуют посредством сил, описываемых классической механикой Ньютона, то есть таких сил, которые равны между собой по модулю, противоположны по направлению и имеют общую линию действия – пространственную прямую, проходящую через обе частицы (силами, вводимыми в причинной механике, пренебрежем вследствие их малости). Такие силы могут быть представлены в форме
где F – модуль сил F1 и F2; (r1-r2)/|r1-r2| – направляющий орт; знаки плюс и минус отвечают случаям соответственно взаимного отталкивания и притяжения частиц. При вычислении неопределенности энергии ограничимся учетом ситуаций, когда «столкнувшиеся» частицы располагаются с точкой столкновения на одной прямой (последняя может быть различной для разных актов «столкновения»). В связи с тем, что в данном случае силы F1 и F2 ориентированы вдоль этой же прямой, направляющий орт в выражении (1.8) совпадает с точностью до знака с векторами (r1-r)/|r1-r| и (r2-r)/|r2-r|, поэтому выражение (1.8) может быть переписано в виде
(здесь и в приводимом ниже равенстве (1.11) знак при F может отличаться от знака в формуле (1.8)). При таком представлении сил F1 и F2 неопределенность значения энергии ΔE, одинаковая для обеих частиц, вычисляется очень просто:
где F΄ – значение F в некоторой средней точке; i = 1, 2; здесь использованы теорема о среднем значении и первое из выражений (1.5). Теперь вычислим неопределенность импульса. Имея целью сравнить получаемый результат с соответствующим результатом квантовой механики, расчет произведем применительно к одномерному случаю, как это делается в [2]. Пусть частицы вместе с точкой столкновения находятся при осуществлении «столкновения» на прямой, параллельной координатной оси z. Тогда силы F1 и F2, описываемые выражением (1.8), могут быть представлены в форме
где k – направляющий орт оси z. В этом случае неопределенность z-компоненты импульса
где F″ — значение F в некоторой средней точке; i = 1, 2; использованы теорема о среднем значении и второе из выражений (1.5). В данном случае неопределенность z-координаты
где z1, z2, z – z‑координаты «столкнувшихся» частиц и точки столкновения. Конкретизируем значения сил F1 и F2. Будем считать, что частицы несут электрические заряды e или –e (–e – заряд электрона), взаимодействуют посредством только электрических сил и при «столкновении» взаимно неподвижны. В этом случае их взаимодействие осуществляется кулоновскими силами, описываемыми выражением (1.8) с модулем
где
Составим произведение модуля сил F и неопределенностей пространственного и временного положений частиц. С учетом зависимостей (1.6), (1.7), (1.14) и определения хода времени с2 имеем
где α = e2/(4peoħc) » 1/137 – постоянная тонкой структуры; ħ = h/(2p); h – постоянная Планка; с – скорость света в вакууме. Очевидно, что в качестве величин F′ и F″, входящих в выражения (1.10) и (1.12), может быть принято рассматриваемое значение модуля сил: F′ » F″ » F. Отсюда и из выражений (1.10), (1.12), (1.13), (1.15) получаем
Одно из соотношений неопределенностей квантовой механики, записанное для минимально возможных значений неопределенностей, имеет вид
Сравнивая второе из соотношений (1.16) с формулой (1.17), находим:
Тот факт, что основная количественная характеристика причинной механики – константа с2 – представляется в виде произведения универсальных постоянных, подтверждает справедливость исходного положения теории Козырева о ее фундаментальности. Указанное численное значение константы с2 согласуется со значением, полученным Н. А. Козыревым экспериментально путем измерения добавочных сил в механических системах [1, с. 367, 382]. То обстоятельство, что опытное значение с2 оказалось именно таким, позволило ученому принять зависимость |с2| = αc в качестве эмпирического факта. Результат, выражаемый соотношениями (1.18), позволяет по-новому взглянуть на некоторые положения квантовой механики. Ученых-физиков давно волнует происхождение фундаментальной безразмерной константы α – постоянной тонкой структуры. Так, Р. Фейнман пишет: «Вам, конечно, хотелось бы узнать, как появляется это число [...]? Никто не знает. Это одна из величайших проклятых тайн физики: магическое число, которое дано нам и которого человек совсем не понимает» [3, с. 114]. Соотношения (1.18) приподнимают завесу тайны над этим числом. Благодаря им, говоря словами Н. А. Козырева, «наличие безразмерной постоянной α перестает быть загадочным и становится естественным как отношение некоторых двух [фундаментальных] скоростей» [1, с. 367]. Выражения (1.18) позволяют также уточнить и дать новую интерпретацию соотношению неопределенностей для энергии и времени. Это соотношение применительно к наименьшим возможным значениям неопределенностей обычно записывают в виде
Данное соотношение, в отличие от соотношения (1.17), устанавливает не точную нижнюю границу произведения неопределенностей, а только его порядок. И сами входящие в (1.19) величины трактуются иначе, нежели величины, фигурирующие в (1.17). Это связано с тем, что в квантовой механике время t считается детерминированной, а не случайной переменной, поэтому величины ∆E и ∆t понимаются не в обычном смысле, как среднеквадратические отклонения, а соответственно как погрешность измерения энергии и как длительность процесса ее измерения [4, с. 317; 5]. Нетрудно видеть, что различие в трактовках квантовомеханических зависимостей (1.17) и (1.19) противоречит релятивистской симметрии пространства и времени. Выражения (1.18) позволяют устранить это противоречие. Они и первое из равенств (1.16) приводят к соотношению неопределенностей для энергии и времени в «стандартной» форме, связывающей минимально возможные значения среднеквадратических отклонений соответствующих переменных:
Выражения (1.18) вместе с (1.15) дают еще одно соотношение неопределенностей:
где слева стоит величина, имеющая размерность действия. Ограничения на возможные значения величин ∆r и ∆t можно получить, если принять условие, что неопределенность энергии не превосходит энергию покоя электрона:
где me – масса электрона. Данное условие и выражения (1.6), (1.7), (1.14), (1.20), (1.21) приводят к следующим неравенствам:
здесь величина, стоящая в правой части первого неравенства, равна половине так называемого классического радиуса электрона. В настоящем разделе мы отошли от важного для причинной механики подразделения взаимодействующих материальных точек на причину и следствие (различающихся, в частности, тем, что следствие всегда наступает позже причины). В приведенных выше рассуждениях взаимодействующие частицы рассматриваются как эквивалентные, и их нельзя объективно разделить на причину и следствие; к примеру, их временные координаты при «столкновении» удовлетворяют с равной вероятностью как неравенству t1 > t2 , так и неравенству t2 > t1. Воспользовавшись соотношением неопределенностей (1.17), мы доказали справедливость закона Козырева (1.2) и подтвердили, что ход времени с2 имеет именно то значение, которое Н. А. Козырев приписывал ему на основании результатов макроскопических экспериментов. Легко убедиться в том, что если изменить ход рассуждений и принять в качестве исходного постулата закон (1.2) с константой с2, даваемой выражениями (1.18), то с помощью приведенных рассуждений можно придти к соотношениям неопределенностей (1.17), (1.20), (1.21). Это означает, в частности, что квантовомеханические соотношения неопределенностей могут рассматриваться как следствие постулатов причинной механики. Таким образом, содержание настоящего раздела позволяет заключить, что причинная механика Козырева находится в согласии с квантовой физикой. Более того, причинная механика приводит к новой интерпретации соотношений неопределенностей Гейзенберга: эти соотношения оказывается возможным трактовать как следствие того обстоятельства, что при «столкновении» частиц пространственное и временное расстояния между ними имеют неопределенности, подчиняющиеся закону (1.2) с константой с2, равной по модулю αс. Такая трактовка, очевидно, может привести к изменению взгляда и на другие концептуальные положения квантовой механики. 2. О характеристике времени с2 в теории Н. А. Козырева Эксперимент по измерению хода времени с2 проводился Н. А. Козыревым путем взвешивания вращающегося гироскопа с вертикально ориентированной осью [1]. При введении в систему весы–гироскоп вертикальных вибраций наблюдалось изменение веса гироскопа на величину ∆Ф, пропорциональную его весу Ф и линейной скорости вращения ротора v; значение параметра с2 вычислялось из формулы
и оказалось приблизительно равным 2200 км/с [1, с. 366 – 367, 382]. Н. А. Козырев трактовал данный факт как появление в системе добавочных сил, не учитываемых классической механикой. Ученый постулировал, что с2 есть псевдоскаляр, так как при замене исследуемой физической системы на зеркально симметричную эффект менял знак. Ход времени с2 определяется в причинной механике как скорость реализации причинного воздействия в элементарном причинно-следственном звене, состоящем из двух материальных точек — точки-причины и точки-следствия:
где Данное определение придает важнейшей в причинной механике характеристике времени ясный физический смысл. Оправданность введения именно такого определения подкрепляется результатами предыдущего раздела, в котором доказано, что величина с2 есть фундаментальная константа. Однако приведенное определение все же обладает рядом недостатков. 1. Ход времени с2 определяется равенством (2.2) через величины 2. Равенство (2.2) не отвечает псевдоскалярному характеру с2 (принимаемое Н. А. Козыревым допущение о псевдоскалярности временного интервала 3. Рассматриваемое определение приводит к несогласованности между проявляющейся в астрономических наблюдениях [6, 7] мгновенности передачи воздействия через время на космические расстояния и конечностью скорости передачи такого воздействия в элементарном причинно-следственном звене. 4. В [1] не проведено строго логического перехода от определения (2.2) к формуле для добавочных сил (2.1) (такой переход, скорее всего, в принципе невозможен, так как, располагая единственной скалярной величиной с2, нельзя сделать однозначного заключения о значении векторной величины, каковой является добавочная сила), поэтому фигурирующая в формуле (2.1) величина с2, вообще говоря, не обязана совпадать с величиной, определяемой равенством (2.2). В связи с тем, что приведенное определение имеет указанные недостатки, представляется целесообразным дать иное определение хода времени, которое сохраняло бы наиболее существенные черты величины с2, описанные в [1], но было бы лишено отмеченных недостатков. Такое определение предлагается ниже.
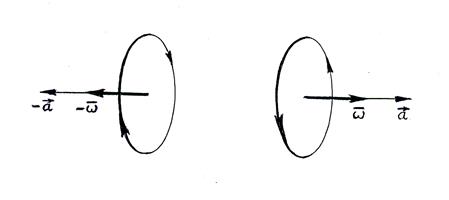
В соответствии с положениями причинной механики будем считать, что время посредством своих активных свойств по-разному взаимодействует с правыми и левыми физическими системами. Одним из простейших математических объектов, различающих правое и левое, является пара (а, ω) коллинеарных между собой вектора a и псевдовектора ω (рис. 2.1). (Простой пример: движение в направлении, указываемом вектором a, с одновременным вращением в сторону, определяемую псевдовектором ω, является правовинтовым при совпадении направлений а и ω и левовинтовым, когда направления а и ω взаимно противоположны.) Допустим, что ход времени описывается именно таким математическим объектом. Тогда он, очевидно, может проявляться в физических системах, кинематика которых характеризуется аналогичной парой векторов. Как раз такой случай реализован в описанном выше опыте с вибрирующим гироскопом, где такую кинематическую пару образуют вызываемое вибрацией ускорение гироскопа а = аk и угловая скорость его вращения ω= ωk (здесь а – скаляр, ω – псевдоскаляр, k – направляющий орт оси вращения).
Показанное направление псевдовектора ωсоответствует в правой системе координат отмеченному направлению обхода окружности.
Можно предположить, что воздействие физических свойств времени на гироскоп приводит к появлению добавок ∆а и ∆ω к величинам а и ω, которые являются монотонными функциями этих величин, удовлетворяют условию ∆а = ∆ω = 0 при aω = 0 и имеют знаки, зависящие от взаимной ориентации векторов а и ω. Тогда в линейном по а и ω приближении можем записать:
где ka и kω – некоторые размерные коэффициенты; знаки выражений положительны при одной взаимной ориентации векторов a, ω и отрицательны при другой их взаимной ориентации. При вибрировании гироскопа ускорение a периодически меняет знак, а угловая скорость ω остается неизменной. При этом среднее по времени значение добавки ∆а оказывается отличным от нуля, несмотря на равенство нулю среднего значения ускорения а. Это связано с тем, что знак ∆а одинаков на любом полупериоде вибрации в силу зависимости его как от знака а, так и от взаимной ориентации а и ω, изменяющейся вместе с изменением знака а. Умножая среднее значение ∆а на массу ротора гироскопа, получаем среднее значение добавочной силы, действующей на гироскоп:
здесь использовано соотношение Сравним выражение (2.4) с полученным экспериментальным путем соотношением (2.1). Видно, что выражение (2.4) включает в себя ту же, что и соотношение (2.1), зависимость добавочной силы от линейной скорости вращения ротора v и от веса гироскопа Итак, мы подтвердили справедливость первого из равенств (2.3). Ясно, что коэффициент ka, входящий в это равенство, может зависеть от характеристик вибрации и размеров гироскопа. Допустим, что второе равенство в (2.3) тоже верно и коэффициент kω в нем зависит от свойств системы в точности так, как и коэффициент ka (в [1] измерения ∆ω не проводились, поэтому мы не можем сопоставить это допущение с опытными данными). Тогда отношение ∆a/∆ω представляет собой псевдоскаляр, имеющий размерность скорости и не зависящий от конкретных свойств изучаемой физической системы. Величину ∆a/∆ω естественно и принять в качестве хода времени c2. Легко убедиться в том, что определяемая таким образом величина c2 лишена отмеченных ранее недостатков, которые свойственны определению ее, базирующемуся на равенстве (2.2). Предложенный подход к определению хода времени допускает распространение на физические системы, не связанные с вращающимися телами. Для таких систем роль пары (a, ω) в определении c2 будут играть другие величины, например, плотность потока энергии и плотность объемных моментов сил.
Примечание. Содержание настоящего раздела было изложено в виде рукописной заметки в апреле 1979 года и тогда же обсуждено с Н. А. Козыревым. Им были сделаны следующие два замечания. 1. В схеме, изображенной на рис. 2.1, в случае, когда a — ускорение, на систему действует нескомпенсированная сила, что ведет к нарушению закона сохранения импульса. Между тем, справедливость этого закона была проверена с большой точностью в специальных опытах, когда и источник вибрации, и гироскоп помещались на одну чашу весов. В таких опытах добавочные силы не регистрировались. 2. Формула (2.4) содержит радиус ротора R. Чтобы привести ее к виду (2.1), нужно принять, что ka ~ R. Но в этом случае не ясен физический смысл формулы (2.3). Опыты с гироскопами, у которых ротор имел форму тонкостенного стакана (так что с хорошей точностью выполнялось условие R = const), а также анализ асимметрии фигур планет и исследование широтной зависимости эффекта изменения веса гироскопа убеждают в том, что в формуле (2.4) должно стоять не отношение v/R =
Рис. 2.2. Возможная система векторов для двух взаимодействующих объектов
Ответом на первое замечание Н. А. Козырева служит рис. 2.2, на котором изображена возможная система векторов для причинно-следственного звена в целом. Видно, что в такой системе отсутствуют нескомпенсированные силы, и закон сохранения импульса выполняется. Ответа на второе замечание автор не имеет. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и временнм
и временнм  различиями, отношение которых есть фундаментальная константа, называемая ходом времени с2:
различиями, отношение которых есть фундаментальная константа, называемая ходом времени с2: (1.1)
(1.1)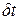 . Однако утверждение о псевдоскалярности
. Однако утверждение о псевдоскалярности 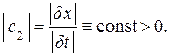 (1.2)
(1.2) (1.3)
(1.3) (1.4)
(1.4) (1.5)
(1.5)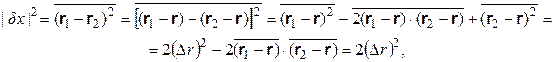
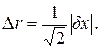 (1.6)
(1.6)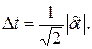 (1.7)
(1.7)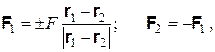 (1.8)
(1.8)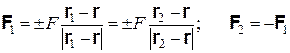 (1.9)
(1.9) (1.10)
(1.10) (1.11)
(1.11)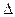 pz, совпадающая для обеих частиц, составляет
pz, совпадающая для обеих частиц, составляет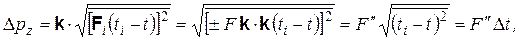 (1.12)
(1.12)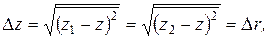 (1.13)
(1.13)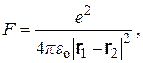
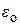 – электрическая постоянная. В последующем изложении используется только такое значение модуля сил, которое отвечает расстоянию между частицами |r1-r2|, равному |
– электрическая постоянная. В последующем изложении используется только такое значение модуля сил, которое отвечает расстоянию между частицами |r1-r2|, равному | 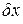 |. Именно это значение модуля сил далее обозначается символом F:
|. Именно это значение модуля сил далее обозначается символом F: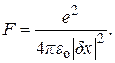 (1.14)
(1.14) (1.15)
(1.15)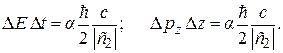 (1.16)
(1.16)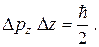 (1.17)
(1.17)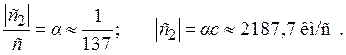 (1.18)
(1.18)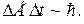 (1.19)
(1.19) (1.20)
(1.20)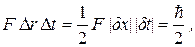 (1.21)
(1.21)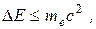 (1.22)
(1.22)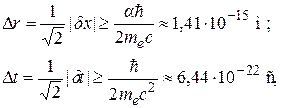 (1.23)
(1.23) (2.1)
(2.1)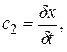 (2.2)
(2.2)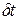 – сколь угодно малые, но не равные нулю пространственное и временне различия между точкой-причиной и точкой-следствием.
– сколь угодно малые, но не равные нулю пространственное и временне различия между точкой-причиной и точкой-следствием. Рис. 2.1. Пара коллинеарных вектора а и псевдовектора ω
Рис. 2.1. Пара коллинеарных вектора а и псевдовектора ω (2.3)
(2.3)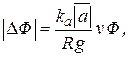 (2.4)
(2.4)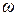 = v/R, кроме того, масса ротора приравнена к массе всего гироскопа
= v/R, кроме того, масса ротора приравнена к массе всего гироскопа  /g, как это сделано в [1]; R и v – некоторые средние значения радиуса ротора и линейной скорости его вращения;
/g, как это сделано в [1]; R и v – некоторые средние значения радиуса ротора и линейной скорости его вращения;