
|
|
Закон композиции одинаково направленных анизотропных скоростейПусть в системах выполняется одинаковая анизотропия скоростей светового сигнала, то есть, имеем равенства
где относительные скорости удовлетворяют равенству
Закон композиции одинаково направленных абсолютных анизотропных скоростей имеет вид
Рассмотрим третью систему
Множество абсолютных скоростей образует абелеву группу с коммутативным законом композиции элементов группы Для закона выполняется свойство ассоциативности
Единичный элемент группы находим из формулы
Таким образом, единичный элемент соответствует значению Из закона композиции
следует выражение обратного элемента
Элементы группы являются самосопряженными. Выпишем некоторые равенства
Параметр анизотропии
и представляется в прямых преобразованиях через скорости
Отметим некоторые работы [20, 21, 23-25], в которых рассматривался закон композиции вида (3.7) с различных точек зрения. Закон композиции анизотропных скоростей (3.7) для типа I вытекает из равенства (2.9). В случае типов II и III имеем, согласно преобразований, соответствующие равенства
из которых вытекают следующие законы композиций
Для типа IV имеем обычный закон сложения скоростей в классической физике
При
Заключение В работе рассматривается локально анизотропная (плоская) финслерова геометрия с двумя скалярными параметрами
БИБЛИОГРАФИЧЕСКИЙ СПИСОК 1. Poincare, H. La mesure du temps / H. Poincare // Rev. Metaphys. Mordle, 1898. – V. 6. – P.1-13. 2. Poincare, H. Surla dynamique de l’ectron / H. Poincare // Rend. Circolo Mat. Palermo, 1906. – V.21. – P.129-176. 3. Minkowski, H.I. “Raum und Zeit”, address delivered at the 80th Assembly of German Scientiests and Physicians (Köln, 1908) / H.I. Minkowski // Phys. Ztscht, 1909. – Bd.10. – P.104-134. 4. Лобачевский, Н.И. Полное собрание сочинений [Текст], т. II. / Н.И. Лобачевский. – Москва-Ленинград: Гостехиздат, 1949. – 304 с. 5. Фок, В.А. Теория пространства, времени и тяготения [Текст] / В.А. Фок. – Москва: Гостехиздат, 1955. - 241 с. 6. Rund, H. The Differential Geometric of Finsler Spaces / H. Rund. - Berlin: Springer-Verlag, 1959. – 396 p. 7. Busemann, H. Metric Methods in Finsler Spaces and in Foundations of Geometric / H. Busemann. - Princeton: Princeton University Press, 1942. – 241 p. 8. Pimenov, R.I. Kinematics Spaces (Mathematical Theory of Space-time / R.I. Pimenov. - New-York: Plenum Press, 1970. – 93 p. 9. Asanov, G.S. Finsler Geometry, Relativity and Gange Theories / G.S. Asanov. - Dordrecht: D.Reidel Publ. – Comp., 1985. – 370 p. 10. Matsumoto, M. Foundations of Finsler Geometry and Special Finsler Spaces / M. Matsumoto. - Otsu, Japan: Kaiseisha Press, 1986. 11. Пименов, Р.И. Анизотропное финслерово обобщение теории относительности как структуры порядка [Текст] / Р.И. Пименов. –Сыктывкар: Изд-во Коми филиала АН СССР, 1987. – 184 с. 12. Богословский, Г.Ю. Теория локального анизотропного пространства-времени [Текст] / Г.Ю. Богословский. – М.: Изд-во МГУ, 1992. –271 с. 13. Асанов, Г.С. Финслероидная геометрия [Текст] / Г.С. Асанов. – Москва: Изд-во МГУ, 2004. - 160 с. 14. Reichenbach, H. Axiomatik der relativistischen Raum-Zeit-Lehre / H. Reichenbach. – Braunschweig: F. Vieweg & Sons, 1924. - 302 s. 15. Grunbaum, A. Philosophical Problem of Space and Time / A. Grunbaum. – New York: Alfred A.Knopf, 1963. 16. Зарипов, Р.Г. К определению одновременности в специальной теории относительности [Текст] / Р.Г. Зарипов // Гравитация и теория относительности. – Казань: Изд-во КГУ, 1978. – Вып. 14-15. – С. 60-69. 17. Зарипов, Р.Г. О физическом понятии отношения одновременности [Текст] / Р.Г. Зарипов // Гравитация и теория относительности. – Казань: Изд-во КГУ, 1980.– Вып. 17.– С. 47-51. 18. Zaripov, R.G. Convention in the Definition of Geometry of Space-Time / R.G. Zaripov // Galilean Electrodynamics, 2000. – V.11. – №4. – P.63-68. 19. Асанов, Г.С. Класс сферически симметричных финслеровых метрических функций с индикатрисой постоянной кривизны [Текст] / Г.С. Асанов // Вестн. Моск. ун-та. Физ. Астрон., 1993. – №3. – С. 74-75. 20. Asanov, G.S. Finslerian Extension of Lorentz Transformations / G.S.Asanov // Rep. Math. Phys., 1998. – V.42. – №3. – P. 273-296. 21. Ляховицкий, В.М. Специальная теория относительности (одномерный случай) без постулата о равномерности направлений [Текст] / В.М. Ляховицкий // Препринт ИТЭФ. 87-45. 1987. 12 с. 22. Bogoslovsky, G.Yu. A Special Relativistic Theory of the Locally Anisotropic Space-Time, I: The Metric and Group of Motion of the Anisotropic Space of Events / G.Yu. Bogoslovsky // Nuovo Cimento, 1977. – V. 40B. –P. 99-115. 23. Petryszyn, H. On a certain group-kinematical method of generalization Lorentz transformations in two-dimensional space-time / H. Petryszyn // Wroclaw: Instytut Mathematyki i Fizyki Theoretyczney Politechniki Wroclawskiey Kamunikaty, 1973. – №12. – P. 1-26. 24. Болтянский, В.Г. Анизотропный релятивизм [Текст] / В.Г. Болтянский // Дифференциальные уравнения. – 1974. – Т. 10. – с. 2101-2110. 25. Стрельцов, В.И. Об определении одновременности в специальной теории относительности [Текст] / В.И. Стрельцов // Препринт ОИЯИ. – Р2-6928. – 1973. – 10 c. 26. Клейн, Ф. Неевклидова геометрия [Текст] / Ф. Клейн. – Москва-Ленинград: ОНТИ, 1936. – 101 с. 27. Edwards, W.F. Special relativity in anisotropic space [Текст] / W.F. Edwards // Am. J. Phys., 1963. – V.31. – №7. – P. 482-489. 28. Podlaha, M. Lorentz Theory, Palacios Theory and Interferometrical Experiments [Текст] / M. Podlaha // Nuovo Cimento, 1969. – V. 64B. – №1. – P. 181-187. 29. Winnie, J.A. Special relativity without one-way velosity assumptions [Текст] / J.A. Winnie // Phyl. Sci., 1970. – V.37. – №1. – P.81-99; 1970. – V. 37. – №2. – P. 223-238. 30. Mansouri, R. A test theory of special relativity / R. Mansouri, R.U. Sexl // Gen. Rel. Grav., 1977. – V.8. – №7. – P. 497-513, P. 515-524; V.8. – №10. – P. 809-814. 31. Sjodin, T. Synchronization in special relativity and related theories / T. Sjodin // Nuovo Cimento, 1979. – V. 51. – №2. – P. 229-246. 32. Зарипов, Р.Г. Отношение одновременности и финслерова структура плоского анизотропного пространства-времени [Текст] / Р.Г. Зарипов // Гравитация и теория относительности. – Казань: Изд-во КГУ, 1992. – Вып. 29. – С. 64-71. 33. Anderson, R. Conventional of Synchronisation, Gauge Dependenc and Test Theories of Relativity / R. Anderson, I. Vetharanian, G.E. Stedman // Phys. Reports, 1998. – V. 295. – P. 93-180. 34. Николенко, В.Г. Поиски относительной анизотропии скорости света и скорости нейтронов [Текст] / В.Г. Николенко, А.Б. Попов, Г.С. Самосват // ЖЭТФ. – 1979. –– Т. 79, вып. 2. – С. 393-401.
УДК 514.12 ©2005 г., А.В. Коротков 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
,  и
и  . Тогда прямые и обратные преобразования в типе I запишутся так
. Тогда прямые и обратные преобразования в типе I запишутся так ,
,  , (3.1)
, (3.1) , (3.2)
, (3.2) ,
,  , (3.3)
, (3.3) , (3.4)
, (3.4) . (3.5)
. (3.5) . (3.6)
. (3.6) , которая движется вдоль положительного направления со скоростью
, которая движется вдоль положительного направления со скоростью  и
и  относительно систем
относительно систем  и
и 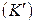 , соответственно. Тогда используя преобразования между
, соответственно. Тогда используя преобразования между  и
и  , окончательно получим закон композиции относительных одинаково направленных анизотропных скоростей
, окончательно получим закон композиции относительных одинаково направленных анизотропных скоростей . (3.7)
. (3.7)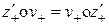 .
. (3.8)
(3.8) . (3.9)
. (3.9) .
. ,
,  (3.10)
(3.10) . (3.11)
. (3.11) ,
, 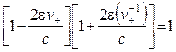 , (3.12)
, (3.12)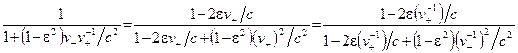 , (3.13)
, (3.13) ,
,  , (3.14)
, (3.14) . (3.15)
. (3.15) (3.16)
(3.16) , (3.17)
, (3.17) , (3.18)
, (3.18) (3.19)
(3.19) (3.20)
(3.20) отражает отличие обратного элемента
отражает отличие обратного элемента  от противоположного
от противоположного 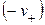 . Скорости света
. Скорости света  и
и  не имеют обратных элементов
не имеют обратных элементов  и
и  в силу нарушения дополнительного условия в (3.10). Поэтому они не входят в множество скоростей, а (3.14) есть формальное равенство. Закон композиции имеет вид
в силу нарушения дополнительного условия в (3.10). Поэтому они не входят в множество скоростей, а (3.14) есть формальное равенство. Закон композиции имеет вид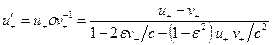 (3.21)
(3.21) и
и 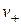 . Причем в обратных преобразованиях, согласно (2.15), справедливо равенство
. Причем в обратных преобразованиях, согласно (2.15), справедливо равенство  . Из (3.21) получим
. Из (3.21) получим  , что в итоге приводит к соотношениям
, что в итоге приводит к соотношениям ,
,  . (3.22)
. (3.22) , (3.23)
, (3.23) , (3.24)
, (3.24) , (3.25)
, (3.25) . (3.27)
. (3.27) и
и 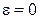 имеем законы композиции скоростей в плоских геометриях типа I, II и III, к которых аксиома параллельных сохраняется [26].
имеем законы композиции скоростей в плоских геометриях типа I, II и III, к которых аксиома параллельных сохраняется [26]. и
и  , зависящими от элементов временной матрицы перехода между событиями, а также от инварианта
, зависящими от элементов временной матрицы перехода между событиями, а также от инварианта  . Найдены четыре принципиально различных типа двумерного финслерова пространства-времени. Исследуются групповые свойства композиции одинаково направленных анизотропных скоростей произвольных сигналов. Анизотропия физических скоростей света не устраняется какими-либо преобразованиями координатной сетки, чем отличаются полученные новые преобразования временного интервала и пространственного расстояния от некоторых известных преобразований для координатного представления анизотропии [25, 27-32]. Обзору таких подходов к проблеме одновременности посвящена работа [33]. Следует также отметить и попытку экспериментального обнаружения относительной анизотропии однонаправленных скоростей света и нейтронов [34].
. Найдены четыре принципиально различных типа двумерного финслерова пространства-времени. Исследуются групповые свойства композиции одинаково направленных анизотропных скоростей произвольных сигналов. Анизотропия физических скоростей света не устраняется какими-либо преобразованиями координатной сетки, чем отличаются полученные новые преобразования временного интервала и пространственного расстояния от некоторых известных преобразований для координатного представления анизотропии [25, 27-32]. Обзору таких подходов к проблеме одновременности посвящена работа [33]. Следует также отметить и попытку экспериментального обнаружения относительной анизотропии однонаправленных скоростей света и нейтронов [34].