|
|
О возможности мгновенного перемещенияВ пространстве-времени Общей Теории Относительности Цель доклада – теоретический анализ возможности: 1) мгновен-ного перемещения материальных частиц; 2) мгновенной передачи сигнала в пространстве-времени Общей Теории Относительности (ОТО).
Математической базой ОТО служит четырехмерное искривленное (псевдориманово) пространство, или иначе – пространство-время. Решение проблемы реализуется с помощью теории физических наблюдаемых величин – хронометрических инвариантов (сокращенно – х.и.) [1, 2]. В терминах физических наблюдаемых квадрат четырехмерного интервала
где
где Частицы с ненулевой массой покоя Частицы с нулевой массой покоя (поля) распространяются вдоль мировых линий нулевой длины ( Условие мгновенного перемещения частицы (или распространия поля) определяется как равенство нулю интервала наблюдаемого времени:
где
то есть мгновенное перемещение (телепортация) вещественной частицы реализуется вдоль чисто пространственных траекторий – мировых линий мнимой длины. Необходимое условие возможности телепортации – наличие вращения трехмерного пространства с точки зрения наблюдателя: Полученная метрическая форма является отрицательно определенной ( Телепортация светоподобных частиц (фотонов) реализуется в пространстве, описываемом метрикой
Она представляет собой конус в пространстве телепортации вещественных частиц, который можно назвать «время-пространство». Телепортируемые фотоны движутся вдоль образующих этого конуса подобно тому, как обычные фотоны движутся вдоль образующих светового конуса, существующего в каждой точке пространства-времени ОТО. Из этой формулы следует, что метрика Нуль-пространство простирается в области, для которой Таким образом, телепортация вещественных частиц и фотонов осуществляется в разных областях подобно тому, как и в обычном пространстве-времени перемещения вещественных частиц и фотонов происходят по-разному: первые движутся внутри изотропного конуса, вторые – вдоль его образующих. Иными словами, телепортация вещественной частицы аналогична ее переходу из пространства во время, тогда как телепортация фотона аналогична ее выходу за пределы обычного пространства-времени.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК 1. Zelmanov, A.L. Chronometric invariants. Dissertation, 1944. First published / A.L. Zelmanov. – CERN, EXT-2004-117, 236 p. 2. Зельманов, А.Л. Хронометрические инварианты и сопутствующие координаты в Общей Теории Относительности [Текст] / А.Л. Зельманов // Доклады АН СССР. – 1956. – Т. 107(6). - с. 815-818. 3. Rabounski, D.D. Particles here and beyond the Mirror. Editorial URSS / D.D. Rabounski, L.B. Borissova. – Moscow, 2001 - 84 p. 4. Borissova, L.B. Fields, vacuum, and the mirror Universe. 2nd revised edition / L.B. Borissova, D.D. Rabounski. – Geneve: CERN, EXT-2003-025. - 272 p.
УДК 530.1 ©2005 г., С.М. Коротаев, Ю.А. Горохов, В.О. Сердюк
ОБРАТИМОСТЬ В НЕОБРАТИМОМ ВРЕМЕНИ
1. Введение. Работы Н.А. Козырева, посвященные развитию нового физического направления – причинной механики [1-4], встретили в свое время, в целом, негативную реакцию. Хотя основной постулат причинной механики – признание фундаментальной необратимости времени выглядит естественно, логические и экспериментальные выводы были настолько неожиданны (при слабо формализованной теории и не слишком строгой постановке экспериментов), что они не могли быть восприняты. После Н.А. Козырева некоторые его результаты были успешно воспроизведены в различных лабораториях (например, [5-7]), но это не изменило ситуацию ввиду нечеткости формулировки проверяемой гипотезы и нестрогости экспериментов. Один из важнейших результатов причинной механики заключается в том, что несимметричное (необратимое) время является активной субстанцией, через него осуществляется универсальное взаимодействие изолированных диссипативных процессов любой природы, причем это взаимодействие идет как с запаздыванием, так и с опережением. Последнее дает возможность, в некотором смысле, наблюдать будущее как существующую реальность. Этот вывод поразителен сам по себе и парадоксален логически, поскольку исходным постулатом являлось как раз наиболее радикальное утверждение о необратимости (обычно обратимость считается свойством не времени, а «частных» систем). В настоящей работе кратко описываются результаты экспериментального развития этих идей, касающиеся взаимодействия процессов в обратном времени. 2. Макроскопическая нелокальность. К началу 90-х годов аксиоматику причинной механики, в том числе само понятие причинности, удалось формализовать [8]. Далее анализ показал, что свойства козыревского взаимодействия диссипативных процессов феноменологически подобны свойствам квантовых нелокальных корреляций [9]. В частности, интерпретация квантовой нелокальности в рамках теории прямого межчастичного взаимодействия Уилера-Фейнмана [10] обосновывает существование сигналов в обратном времени. Это ведет к наблюдаемости опережающих корреляций неизвестных состояний [11] или, иначе выражаясь, случайных процессов. Появилась идея об асимптотическом сохранении квантовых корреляций в сильном макропределе, проверенная в численном [12] и реальном [13] экспериментах. Был обнаружен новый путь формирования запутанных состояний через общий термостат (которым может служить электромагнитное поле) и этот путь требует диссипативности квантово-коррелированных процессов. Это означает, что диссипативность может не только вести к декогеренции, но и, напротив, играть конструктивную роль. Наша идея состояла во включении диссипативности в рамках квантовой теории прямого межчастичного взаимодействия [14], аксиоматика которой математически сходна с аксиоматикой причинной механики [9,15]. Это позволило предложить следующий вид уравнения макроскопической нелокальности, описывающем фактические результаты Н.А. Козырева [9,16-18]:
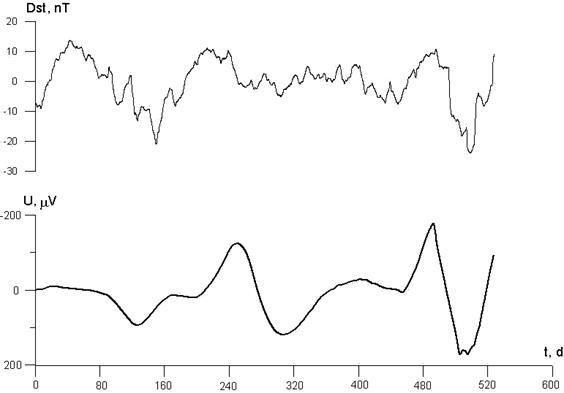
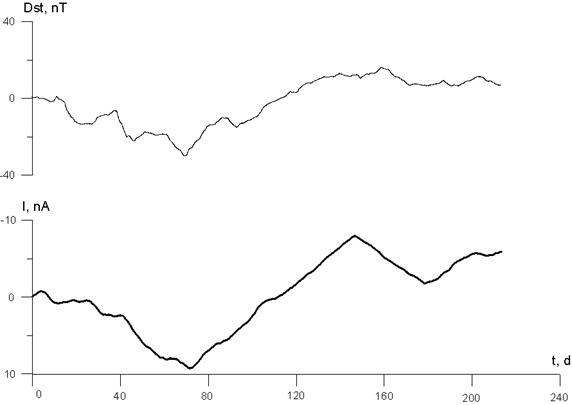
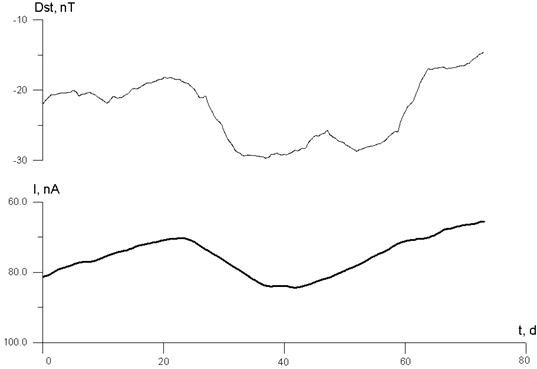
где Данное уравнение в своем простейшем виде не учитывает поглощения промежуточной средой. Его влияние, однако, очень своеобразно. В [14] доказано, что хотя уравнения теории симметричны по времени, фундаментальная асимметрия времени проявляется через асимметрию эффективности поглощения: если запаздывающее поле поглощается полностью, то поглощение опережающего поля, напротив, обязано быть неполным. Это может вести к тому, что уровень опережающих корреляций пробного процесса с процессами – источниками окажется выше запаздывающих. Задачей эксперимента является установление связи изменений энтропии в пробном процессе и процессах-источниках при условии подавления всех классических воздействий (температура, электромагнитное поле и т.д.). В настоящее время созданы две экспериментальные установки – ИГЭМИ и ЦПФ. В первой используются детекторы нелокальных корреляций на основе процессов спонтанных вариаций собственных потенциалов слабополяризующихся электродов в электролите и темновой эмиссии фотокатода. Во второй используется детектор на основе флуктуаций подвижности ионов электролита. Теория детекторов позволяет связать измеряемый сигнал с производством энтропии в пробном процессе, т.е. рассчитывать левую часть уравнения макроскопической нелокальности и осознано принять исчерпывающие меры по подавлению локальных помех. Детальное описание техники и методики экспериментов приведено в [9, 16, 17, 19-21]. В качестве процессов – источников использовались крупномасштабные гелиогеофизические процессы с большой случайной составляющей, а также напротив – детерминированные лабораторные процессы (фазовые переходы). Поскольку, в последних наблюдается только запаздывающая корреляция [20], далее рассматриваются только первые. При этом дается сводка результатов предыдущих (1993-97 гг.) экспериментов [9, 16-19, 21-24] и подробнее приводятся некоторые результаты последнего (2001-03 гг.) эксперимента на установке ИГЭМИ. 3. Основные результаты предыдущих экспериментов. Сигналы всех детекторов коррелированны. Анализ показал, что они формируются некоторыми общими причинами, но их влияние не может быть локальным. Такими общими причинами оказались (в порядке убывания интенсивности влияния): солнечная, синоптическая, геомагнитная и ионосферная активность. Надежно выделена опережающая реакция сигналов детекторов на эти процессы. Запаздывающая реакция всегда меньше. Порядок величины опережения (и запаздывания) велик – от 10 часов до 100 суток. Величина реакции и время опережения растут с ростом пространственного масштаба процессов-источников. Нелокальный характер корреляции доказан нарушением неравенств типа Белла. Уравнение макроскопической нелокальности количественно проверено на примере процесса геомагнитной активности. Уровень опережающей корреляции позволил продемонстрировать возможность использования эффекта макроскопической нелокальности для прогноза солнечной, геомагнитной и синоптической активности. 4. Новые результаты. Эксперимент 2001-03 гг. является самым длительным целенаправленным экспериментом такого рода. Длительность важна потому, что эффект лучше проявляется на крайне низких частотах. Получен ряд непрерывных наблюдений с электродным детектором U с 22/10/2001 по 27/10/2003 и два ряда с фотокатодным детектором: I1 с 22/10/2001 по 24/06/2003 и I2с 14/07/2003 по 27/10/2003. Дискретизация данных 1 час. Здесь мы коснемся только реакции детекторов на геомагнитную активность. Хотя ее влияние на детекторы меньше прямого влияния солнечной активности (именно через анализ соотношения зависимостей сигнала детектора от этих двух процессов лежит один из способов доказательства нарушения неравенства типа Белла [24]), геомагнитная активность представляет примечательный процесс-источник. Во-первых, детекторы сами по себе совершенно нечувствительны к магнитному полю и, во-вторых, омическая диссипация в источнике поле и вместе с ней – интеграл в правой части уравнения макроскопической нелокальности легко оценивается [9,16,17,19,21,22]. В качестве индекса геомагнитной активности избран Dst – индекс, отражающий наиболее крупномасштабные процессы [23]. Выделение в спектре сигналов части обусловленной Dst ирасчет всех членов уравнения макроскопической нелокальности, оставляя сечение взаимодействие в качестве единственного неизвестного параметра, позволило оценить последнее. По данным фотокатодного детектора получено При изучении опережающей реакции для выделения сигнала, обусловленного случайной компонентой геомагнитной активности применялась фильтрация с подобранными из анализа спектров полосой пропускания: 136 сут. > T > 31,8 сут. для U,365 сут. > T > 31,8 сут. для I1 и T > 31,8 сут. для I2 . Далее рассчитывалась корреляционная функция сигнала детектора с Dst в диапазоне сдвигов времени τ ± 371 сут. (τ < 0, соответствует запаздывающей корреляции r ret , τ > 0 – опережающей r adv). По всем рядам опережающая корреляция надежно превышает запаздывающую. Асимметрия корреляций max | r adv| / max |r ret| составила: 1,20 ± 0,01 для U, 1,10 ± 0,01 для I1 и 1,23 ± 0,002 для I 2 . Главные экстремумы опережающей корреляции равны: – 0,59 ± 0,01 при τ = 130 сут. для U, – 0,952 ± 0,004 при τ = 90 сут. для I1 и – 0,82 ± 0,01 при τ = 130 сут. для I2. Отрицательный знак корреляции соответствует теории [9]. Расхождение между величинами (r, τ) объясняются нестационарностью процесса производства энтропии и диффузии запутанности состояний, а также различными шумовыми свойствами детекторов. Можно сдвинуть реализации Dst и сигналов детекторов на соответствующую величину τ и наглядно убедиться в прогностическом эффекте (рис. 1-3).
Рис. 1. Сигнал электродного детектора U прогнозирует геомагнитную активность Dst с заблаговременностью 130 сут. (t – время в сут. для U)
Рис. 2.Сигнал фотокатодного детектора I (ряд I1) прогнозирует геомагнитную активность Dst с заблаговременностью 90 сут. (t – время в сут. для I)
Рис. 3.Сигнал фотокатодного детектора I (ряд I2) прогнозирует геомагнитную активность Dst с заблаговременностью 130 сут. (t – время в сут. для I) 5. Заключение. Эксперименты на современном уровне строгости подтверждают результаты Н.А. Козырева об удивительном проявлении обратимости в необратимом времени – возможности наблюдения будущих случайных состояний (не детерминированных предшествующей эволюцией). Вместе с тем, уравнение макроскопической нелокальности – пока не более чем эвристическая модель, поэтому развитие последовательной теории крайне актуально. Использование эффекта макроскопической нелокальности для прогноза, в частности, геомагнитной активности уже возможно. БИБЛИОГРАФИЧЕСКИЙ СПИСОК 1. Козырев, Н.А. Избранные труды [Текст] / Н.А.Козырев. - Л.: ЛГУ, 1991. 2. Козырев, Н.А. Проблемы исследования Вселенной [Текст] / Н.А. Козырев,В.В. Насонов.7, 168 (1978). 3. Козырев, Н.А., В.В.Насонов, Проблемы исследования Вселенной, 9, 76 (1980). 4. Козырев, Н.А., Проблемы исследования Вселенной, 9, 85 (1980). 5. D.Savage, in Progress in Space-Time Physics, edited by B.Wesely (Blumberg, 1987), p.242. 6. Лаврентьев, М.М. ДАН [Текст] / М.М. Лаврентьев, И.А. Еганова, В.Г. Медведев, В.К. Олейник, С.Ф. Фоминых, 323(4), 649 (1992). 7. H. Hayasaka and S. Takeuchi, Phys. Rev. Lett., 63,2701 (1989), 8. Korotaev. S.M., Galilean Electrodynamics, 4 (5), 86 (1993). 9. Коротаев, С.М. Физическая мысль России [Текст] / С.М. Коротаев, М.О. Сорокин, В.О. Сердюк, Ю.М. Абрамов, 2, 1 (1998). 10. J.G. Cramer, Phys. Rev. D, 22, (1980). 11. A.C. Elitzur and S.Dolev, in The Nature of Time: Geometry, Physics and Perception, edited by R.Bucceri (Kluwer Academic Publishers, 2003), p.297. 12. D.Home and A.S.Majumdar, Phys. Rev. A, 52, 4959 (1995). 13. S. Gosh, T.F. Rosenbaum, G.A. Aeppll and S.N.Coppersmith, Nature, 425, 48(2003). 14. F. Hoyle and J.V. Narlikar, Rev. Mod. Phys., 67, 113 (1995). 15. S.M. Korotaev, Galilean Electrodynamics, 11(2), 29(2000). 16. S.M. Korotaev, V.O. Serdyuk, and M.O. Sorokin, Galilean Electrodynamics, 11 (2), 23 (2000). 17. S.M. Korotaev, A.N .Morozov, V.O. Serdyuk, and J.V. Gorohov, in Physical Interpretation of Relativity Theory, edited by M.C.Duffy (Moscow: BMSTU Press), p.200. 18. S.M. Korotaev, V.O. Serdyuk, V.I. Nalivaiko, A.V. Novysh, S.P. Gaidash, Yu.V.Gorokhov, S.A.Pulinets and Kh.D.Kanonidi, Phys. Wave Phenomena, 11 (1), 46 (2003). 19. Коротаев, С.М. Геомагнетизм и аэрономия [Текст] / С.М. Коротаев, В.О. Сердюк, М.О. Сорокин, 40 (3), 56 (2000). 20. Коротаев, С.М., Физическая мысль России [Текст] / С.М. Коротаев, В.О. Сердюк, М.О. Сорокин, В.А. Мачинин, 3, 20 (2000). 21. Коротаев, С.М. Известия высших учебных заведений. Физика [Текст] / С.М. Коротаев, А.Н. Морозов, В.О. Сердюк, М.О. Сорокин, 5, 3 (2002). 22. Korotaev, S.M. Phys. Chem. Earth A / S.M. Korotaev, V.O. Serdyuk, M.O. Sorokin and J.M. Abramov, 24 (8), 735 (1999). 23. Необратимые процессы в природе и технике. Труды второй всероссийской конференции [Текст] / С.М. Коротаев, А.Н. Морозов, Ю.В. Горохов, В.И. Наливайко, А.Н. Новыш, С.А. Пулинец, В.О. Сердюк. – М.: МГТУ, 2003, с.12. 24. S.M. Korotaev, V.O. Serdyuk, J.V. Gorohov, S.A. Pulinets and V.A. Machinin, Frontier Perspectives, 13 (1), 42 (2004).
УДК 530.1 ©2005 г., А.Г. Пархомов

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (расстояния) между двумя точками (событиями) принимает вид [1, 2]
(расстояния) между двумя точками (событиями) принимает вид [1, 2]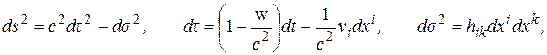

 – интервал наблюдаемого времени;
– интервал наблюдаемого времени;  – гравитационный потенциал;
– гравитационный потенциал; 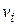 – скорость вращения трехмерного пространства;
– скорость вращения трехмерного пространства;  – наблюдаемый пространственный интервал;
– наблюдаемый пространственный интервал;  – трехмерный наблюдаемый метрический тензор;
– трехмерный наблюдаемый метрический тензор;  – пространственные компоненты фундаментального метрического тензора;
– пространственные компоненты фундаментального метрического тензора;  – (
– (  ). Величину
). Величину  можно также записать как
можно также записать как
 – трехмерная наблюдаемая скорость частицы. Из этой формулы видно, что
– трехмерная наблюдаемая скорость частицы. Из этой формулы видно, что  ; 2) нулевым при
; 2) нулевым при  ; 3) мнимым при
; 3) мнимым при  .
. (вещество) движутся: 1) вдоль вещественных мировых линий (
(вещество) движутся: 1) вдоль вещественных мировых линий ( 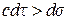 ), обладая при этом вещественной релятивистской массой
), обладая при этом вещественной релятивистской массой  ; 2) вдоль мнимых мировых линий (
; 2) вдоль мнимых мировых линий ( 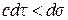 ), обладая при этом мнимой «релятивистской» массой*
), обладая при этом мнимой «релятивистской» массой*  .
.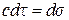 ), называемых изотропными, со скоростью света, обладая при этом отличной от нуля релятивистской массой
), называемых изотропными, со скоростью света, обладая при этом отличной от нуля релятивистской массой  . К светоподобным частицам относятся кванты электромагниного поля (фотоны).
. К светоподобным частицам относятся кванты электромагниного поля (фотоны). . Отсюда следует
. Отсюда следует
 – трехмерная координатная скорость;
– трехмерная координатная скорость;  – скорость света. С учетом этой формулы квадрат интервала для частиц вещества принимает вид
– скорость света. С учетом этой формулы квадрат интервала для частиц вещества принимает вид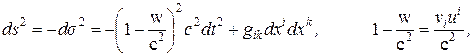
 . Если
. Если  , то пространство коллапсирует:
, то пространство коллапсирует:  . При этом четырехмерное пространство телепортации становится трехмерным:
. При этом четырехмерное пространство телепортации становится трехмерным:  .
. ). Отсюда следует, что
). Отсюда следует, что  является положительно определенной (
является положительно определенной (  ). Таким образом, в терминах физического мира область телепортации выглядит так: 1) трехмерное «пространство» телепортации с метрикой
). Таким образом, в терминах физического мира область телепортации выглядит так: 1) трехмерное «пространство» телепортации с метрикой  ; 2) одномерный «временной» интервал телепортации
; 2) одномерный «временной» интервал телепортации  соответствует трехмерному наблюдаемому пространству с метрикой
соответствует трехмерному наблюдаемому пространству с метрикой  . Последнее означает, что время, в течение которого телепортация осуществляется с точки зрения внутреннего наблюдателя, связанного с телепортируемой частицей, зависит от скорости вращения пространства
. Последнее означает, что время, в течение которого телепортация осуществляется с точки зрения внутреннего наблюдателя, связанного с телепортируемой частицей, зависит от скорости вращения пространства  . С точки зрения реального (внешнего) наблюдателя частица «исчезает» в одной точке и в тот же момент «возникает» в другой («мгновенное» перемещение).
. С точки зрения реального (внешнего) наблюдателя частица «исчезает» в одной точке и в тот же момент «возникает» в другой («мгновенное» перемещение).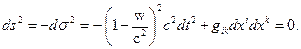
 . Из условия
. Из условия 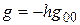 [1, 2] следует, что метрика
[1, 2] следует, что метрика  также в этом случае вырождается:
также в этом случае вырождается:  , что является нарушением сигнатурных условий, определяющих псевдориманово пространство, моделирующее реальный физический мир. Таким образом, телепортация фотонов реализуется вне обычного пространства-времени вдоль траекторий нулевой наблюдаемой длины. Пространство телепортации фотонов, названное нуль-пространство, представляет собой голограмму из стоячих волн, образовавшихся как результат суперпозиции волн, распространяющихся в двух противоположных направлениях во времени (из прошлого в будущее и из будущего в прошлое), являющихся обдновременно нуль-частицами: для них релятивистская масса m = 0 [3, 4].
, что является нарушением сигнатурных условий, определяющих псевдориманово пространство, моделирующее реальный физический мир. Таким образом, телепортация фотонов реализуется вне обычного пространства-времени вдоль траекторий нулевой наблюдаемой длины. Пространство телепортации фотонов, названное нуль-пространство, представляет собой голограмму из стоячих волн, образовавшихся как результат суперпозиции волн, распространяющихся в двух противоположных направлениях во времени (из прошлого в будущее и из будущего в прошлое), являющихся обдновременно нуль-частицами: для них релятивистская масса m = 0 [3, 4]. , то есть в вершине изотропного конуса – месте перехода прошлого в будущее. В пространстве-времени ОТО – это точка, в обобщенном пространстве-времени, допускающем вырождание метрики – это пространство особого типа («голографическое» пространство).
, то есть в вершине изотропного конуса – месте перехода прошлого в будущее. В пространстве-времени ОТО – это точка, в обобщенном пространстве-времени, допускающем вырождание метрики – это пространство особого типа («голографическое» пространство).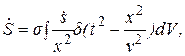
 – производство энтропии в пробном процессе (детекторе),
– производство энтропии в пробном процессе (детекторе),  м2 – сечение взаимодействия, e, m – заряд и масса электрона,
м2 – сечение взаимодействия, e, m – заряд и масса электрона,  м/с – ход времени [1],
м/с – ход времени [1],  – плотность производства энтропии в процессах-источниках, х – расстояние, t – время, v2 ≤ c2, интегрирование ведется по объему источников, δ – функция показывает, что взаимодействие идет с запаздыванием и симметричным по времени опережением. Если взаимодействие идет через среду по межчастичным цепям через микроскопические поля Уилера-Фейнмана, результирующие сдвиги обоих знаков будут велики. В классическом пределе с2→ ∞ [1] эффект исчезает.
– плотность производства энтропии в процессах-источниках, х – расстояние, t – время, v2 ≤ c2, интегрирование ведется по объему источников, δ – функция показывает, что взаимодействие идет с запаздыванием и симметричным по времени опережением. Если взаимодействие идет через среду по межчастичным цепям через микроскопические поля Уилера-Фейнмана, результирующие сдвиги обоих знаков будут велики. В классическом пределе с2→ ∞ [1] эффект исчезает. м2, электродного -
м2, электродного -  м2, т.е. порядка сечения атома в соответствии с теоретической оценкой.
м2, т.е. порядка сечения атома в соответствии с теоретической оценкой.