
|
|
Поле плотности времени в Общей ТеорииОтносительности
В Общей Теории Относительности различаются физическое наблюдаемое время и идеальное координатное время. Физическое время наблюдатель регистрирует на реальных часах, это – отметки вдоль реальной временной оси, свойства которой зависят от физических условий в лаборатории наблюдателя. Идеальное координатное время – это отметки на «идеальной» временной оси, не связанной с наблюдателем. Такое различие является прямым следствием проблемы определения физических наблюдаемых величин в Общей Теории Относительности. Эту проблему в 1944 году решил известный советский ученый Зельманов [1, 2]. Он определил физические наблюдаемые величины как проекции четырехмерных величин на реальную линию времени и реальное трехмерное пространственное сечение наблюдателя, а также разработал математический аппарат для вычисления этих наблюдаемых проекций (математический аппарат хронометрических инвариантов). Другие физики-теоретики 40-х годов тоже вводили в теорию наблюдаемый интервал времени и наблюдаемые координаты (например, см. известную книгу «Теория поля» Ландау и Лифшица [3], которая переиздается с 1939 года). Однако они, ограничившись этим частным случаем, не пришли к созданию общих математических методов для вычисления физических наблюдаемых величин, как это сделал Зельманов. Итак, постановка задачи [4]. Пространство реального наблюдателя, в общем случае, может вращаться, деформироваться и нести в себе гравитационное поле. Поэтому наблюдаемые проекции любой четырехмерной величины будут зависеть от свойств пространства отсчета, в котором находится наблюдатель. Одним из следствий этого является то, что наблюдаемые координаты вдоль реальной линии времени распределены неоднородно – наблюдаемые промежутки времени будут разными в разных точках пространственного сечения в зависимости от величины гравитационного потенциала, вращения пространства и его деформации. Такая постановка задачи дает возможность рассматривать распределение неоднородности наблюдаемых временных координат как отдельное тензорное поле в пространстве-времени Общей Теории Относительности. Результаты решения этой задачи следующие [4]. Отличие наблюдаемого промежутка времени от идеального, при измерении в одной и той же точке пространства, зависит только от оператора проецирования на линию времени – четырехмерного вектора, который зависит от свойств его пространства отсчета. Фактически этот вектор представляет собой четырехмерный вектор-потенциал поля «плотности» наблюдаемого времени подобно четырехмерному вектор-потенциалу электромагнитного поля. Дальнейшее решение схоже с релятивистской электродинамикой. Тензор поля плотности времени получается как четырехмерный ротор вектор-потенциала поля. Наблюдаемые проекции тензора поля мы будем называть по аналогии с наблюдаемыми величинами в релятивистской электродинамике [5]: (1) «электрическая» компонента поля плотности времени – проекция тензора поля на линию времени – представляет собой наблюдаемый вектор гравитационно-инерциальной силы; (2) «магнитная» компонента поля плотности времени, будучи проекцией тензора поля на пространственное сечение, представляет собой наблюдаемый тензор угловых скоростей вращения пространства. Уравнения движения свободной частицы, выраженные через «электрическую» и «магнитную» компоненты поля плотности времени, включают их в виде действующей силы, математическая форма которой полностью аналогична электромагнитной силе Лорентца из релятивистской электродинамики. Таким образом, поле плотности времени действует на свободную частицу точно так же, как электромагнитное поле движет электрический заряд. В частности, если частица движется только вдоль линий времени (покоится относительно наблюдателя на его пространственном сечении), полученные уравнения показывают: (1) обе компоненты поля плотности времени не производят работы по перемещению частицы – частица свободно «падает» вдоль линий времени; (2) в этом случае «электрическая» компонента равна нулю – частица движется вдоль линий времени в результате ее увлечения только «магнитной» компонентой поля плотности времени (вращением пространства). Другим словом, вращение пространства как бы «вкручивает» частицы в линии времени. Поскольку наблюдаемые частицы вместе со всем пространственным сечением движутся из прошлого в будущее, должно существовать некоторое «стартовое» вращение пространства, присутствующее при любых физических условиях. При этом вращение тела отсчета может быть только «добавкой», усиливающей или ослабляющей это стартовое вращение пространства. Интересно, что к подобному выводу ранее пришел известный советский астроном Козырев [6] на основе собственных исследований внутреннего строения звезд. В частности, помимо «стартового» вращения пространства, он пришел к выводу, что дополнительные вращения должны производить неоднородность наблюдаемого времени вокруг массивных вращающихся тел, таких как звезды и планеты. Согласно его выводам, неоднородность времени может быть результатом перераспределения энергии. И, наоборот, перераспределение энергии может производить неоднородность времени. Эти выводы должны лучше проявляться при взаимодействии компонент массивных двойных звезд [7]. Он также был первый, кто использовал термин «поле плотности времени». Интересно, что его выводы, происходя из чистой феноменологии, такой как анализ астрономических наблюдений, никак не связаны с математическим аппаратом Общей Теории Относительности. Козырев искал обоснования своим феноменологическим выводам в классической механике [6]. Продолжая краткое изложение полученных результатов, отметим следующие. Уравнения поля плотности времени были выведены аналогично уравнениям Максвелла. Эти уравнения показали, что источники, индуцирующие поле плотности времени (аналоги зарядов и токов), определяются распределением гравитационного потенциала, вращением и неоднородностью пространства. Был также выведен тензор энергии-импульса поля плотности времени. Его наблюдаемые компоненты (плотность энергии поля, вектор плотности импульса и тензор напряжений) показали, что поле плотности времени – это неоднородная вязкая среда, пребывающая в состоянии ультрарелятивистского газа (при положительной плотности среды ее внутреннее давление также положительно – среда сжимается). На основе полученной формулы для тензора энергии-импульса, была рассмотрена задача о плоской волне поля. В результате получилось, что волны поля плотности времени, как и электромагнитные волны, являются поперечными (колебания происходят перпендикулярно направлению распространения волны). Вычисления волнового давления в поле плотности времени показали, что его основным источником являются внутриатомные процессы (так как скорости вращения в атомах очень велики), тогда как макропроцессы его практически не производят. Согласно полученной формуле, возбуждающийся атом излучает поток импульса поля плотности времени, производя положительное волновое давление поля. Наоборот, при релаксации атом поглощает поток импульса поля плотности времени – волновое давление поля вокруг атома становится отрицательным. Таким образом, эффект поля плотности времени полностью противоположен эффекту электромагнитного поля. Экспериментальные тесты этих выводов могут быть основаны на том, что предсказываемое притяжение/отталкивание, производимое внутриатомными процессами, будучи вне известных эффектов электромагнитного и гравитационного полей, является особенностью только данной теории.
Библиографический список 1. Zelmanov, A.L. Chronometric invariants. Dissertation, 1944. First published / A.L. Zelmanov. – CERN: EXT-2004-117. - 236 p. 2. Зельманов, А.Л. Хронометрические инварианты и сопутствующие координаты в Общей Теории Относительности [Текст] / А.Л. Зельманов // Доклады АН СССР. – 1956. - том 107(6). - с. 815-818. 3. Ландау, Л.Д. Теория поля [Текст] / Л.Д. Ландау, Е.М. Лифшиц. – М.: ГИТТЛ, 1939 (последнее дополненное издание – Butterworth-Heinemann, 1980. - 428 p.). 4. Rabounski, D.D. The new aspects of General Relativity / D.D. Rabounski. Geneve, CERN: EXT-2004-025. - 117 p. 5. Borissova, L.B. Fields, vacuum, and the mirror Universe. 2-nd revised edition / L.B. Borissova, D.D. Rabounski. – Geneve: CERN, EXT-2003. -025. - 272 pages. 6. Kozyrev, N.A. On the possibility of experimental investigation of the properties of time Kozyrev / N.A. Kozyrev // Time in Science and Philosophy. – Prague. – Academia. – 1971. - p.111-132. 7. Kozyrev, N.A. Physical peculiarities of the components of double stars. Colloque «On the evolution of double stars» / Kozyrev, N.A. // Comptes rendus, Communications du Observatoire Royal de Belgique. - ser. B. - no. 17. – Bruxelles. – 1967. - p. 197-202.
УДК 530.1 + 115 + 122 ©2005 г., Л.С. Шихобалов ОСНОВЫ ПРИЧИННОЙ МЕХАНИКИ Н.А. КОЗЫРЕВА* Астроном и мыслитель – Николай Александрович Козырев (2.09.1908 – 27.02.1983) – яркий, самобытный ученый, оставивший после себя большое научное наследие. Еще при жизни ученого его работы по теоретической астрофизике и наблюдательной астрономии снискали мировое признание, о чем свидетельствует, в частности, награждение его Международной академией астронавтики именной золотой медалью. Значительное место в научном наследии Н. А. Козырева занимает основанная им причинная механика – наука о физических свойствах времени [1]. Настоящая работа содержит изложение и критический анализ исходных положений причинной механики Козырева. Методологические основы причинной механики.Теория Козырева базируется на нескольких методологических посылках (гипотезах). Сам Н. А. Козырев не формулирует их в виде отдельных аксиом. Однако идеи, заложенные в них, проходят через всю его теорию, поэтому целесообразно выписать их в явном виде. Первая методологическая посылка состоит в принятии субстанциональной концепции времени. Субстанциональная концепция времени заключается в предположении, что время есть самостоятельное явление природы, существующее наряду с веществом и физическими полями, и оно может каким-то образом воздействовать на объекты нашего Мира и протекающие в нем процессы (причем не исключено и обратное воздействие объектов и процессов на свойства времени). Противоположная — реляционная концепция времени, наоборот, отрицает наличие времени как самостоятельной сущности и трактует его как специфическое свойство физических систем и происходящих с ними изменений [2 – 4 и др.]. Современная физика строится на основе реляционной концепции времени. Однако использование этой концепции не привело пока еще к разрешению всех проблем, связанных с временем. Более того, в физике до сих пор не сформулировано даже сущностное определение времени, а имеются только операционные определения, которые указывают различные способы измерения промежутков времени. В свою очередь, сторонники субстанциональной концепции времени, включая Н. А. Ко-зырева, также не ответили на все вопросы, касающиеся времени, и не дали пока еще строгой математической формализации понятию временнόй субстанции. Поэтому можно констатировать, что ныне как реляционная, так и субстанциональная концепции времени представляют собой, скорее, определенные точки зрения, нежели детально проработанные физические гипотезы. Каждая из них имеет свои положительные стороны. К достоинствам реляционной концепции можно отнести то, что она позволяет исследователям стоять твердо на прочном фундаменте опытных данных и не допускает необузданного полета фантазии. Положительная черта субстанциональной концепции состоит в том, что она оставляет исследователю большую свободу для творческих поисков, что может способствовать успешному разрешению научной проблемы. Следует подчеркнуть, что с позиции современной физики, базирующейся на реляционной концепции времени, принципиально невозможно ни подтвердить, ни опровергнуть положение субстанциональной концепции о существовании временной субстанции, поскольку нельзя доказать наличие или отсутствие того, что в рамках данной научной парадигмы не имеет определения. Отметим, что сам Н. А. Козырев по отношению к времени употреблял термин не «субстанция», а «явление природы». Вторая методологическая посылка, используемая Н. А. Козыревым, может быть сформулирована следующим образом. Время наряду с обычным свойством длительности, измеряемой часами, обладает также другими свойствами. Эти свойства ученый называет физическими или активными, противопоставляя их геометрическому (пассивному) свойству длительности. Данная посылка представляет собой вполне оправданную рабочую гипотезу, так как теория, которая предполагает наличие у времени наряду с длительностью каких-то дополнительных свойств, не может оказаться ошибочной, она лишь рискует оказаться избыточной. Действительно, если реальное время все-таки никакими свойствами кроме длительности не обладает, то, положив в уравнениях этой теории все характеристики, отвечающие дополнительным свойствам, равными нулю, мы получим теорию, предполагающую наличие у времени единственного свойства – длительности. Обратное, подчеркнем, неверно: никакая теория, основанная на представлении об отсутствии у времени иных свойств помимо длительности, не сможет описать правильно реальную действительность, если на самом деле время обладает еще и другими свойствами. Упомянем, что в своей теории Н. А. Козырев никоим образом не ревизует общепринятые представления, касающиеся длительности времени, и пользуется в рассуждениях и расчетах понятием промежутка времени в точности так, как это делается всеми. Третья посылка гласит: физические свойства времени могут быть исследованы экспериментально. Правомочность этой посылки, очевидно, не требует обоснования. Три перечисленные посылки являются, на наш взгляд, наиболее существенными. Они носят, так сказать, стратегический характер. Н. А. Козырев в одной из работ концентрированно формулирует их суть так: «Время представляет собой явление природы с разнообразными свойствами, которые могут быть изучены лабораторными опытами и астрономическими наблюдениями» [1, с. 384]. Следующие две исходные посылки можно отнести к разряду тактических. Первая касается выбора математических моделей для описания объектов нашего Мира. Ученого больше всего интересовали проявления свойств времени в обычной окружающей нас реальности, то есть в условиях, в которых с хорошей точностью выполняются законы классической механики Ньютона. Поэтому Н. А. Козырев считал, что причинная механика может строиться как уточнение классической механики и следовательно может использовать для описания объектов нашего Мира те же математические модели, что и классическая механика Ньютона. В связи с этим в причинной механике принято, что: математическими образами физических объектов являются материальные точки или системы материальных точек; образами их воздействий друг на друга служат векторы сил; ареной, на которой разыгрываются события Мира, служат трехмерное собственно евклидово пространство и время – одномерное, непрерывное и однородное по своему геометрическому свойству длительности. Вряд ли существуют причины, по которым можно было бы заранее, до сравнения результатов теории с опытом, возразить против такого допущения. Вторая тактическая посылка заключается в избрании Н. А. Ко-зыревым аксиоматического метода построения теории. В соответствии с ним причинная механика начинается с принятия постулатов, задающих свойства времени, а затем на их основе выводятся следствия о возможных воздействиях времени на различные физические системы нашего Мира. Использование аксиоматического метода, разумеется, не может вызвать возражений, оно согласуется с общим стремлением ученых, работающих в области точных наук, к логической стройности своих теоретических разработок и восходит к построению геометрии Евклидом и механики Ньютоном. Постулаты причинной механики.Н. А. Козырев формулирует следующие три постулата о физических свойствах времени [1, с. 337]. Постулат I.Время обладает особым свойством, создающим различие причин от следствий, которое может быть названо направленностью или ходом. Этим свойством определяется отличие прошедшего от будущего. Постулат II.Причины и следствия всегда разделяются пространством. Поэтому между ними существует сколь угодно малое, но не равное нулю, пространственное различие dx . Постулат III.Причины и следствия различаются временем. Поэтому между их проявлением существует сколь угодно малое, но не равное нулю, временное различие dt определенного знака (знак dt находится из условия, что следствие всегда наступает позже причины). Постулат I, устанавливая наличие тесной связи времени и причинности, немедленно приводит к важному выводу, что на практике искать проявления активных свойств времени следует в причинно-следственных отношениях между явлениями нашего Мира. Принятие этого постулата в качестве начального положения теории свидетельствует о том, что при ее создании Н. А. Козырев ставил целью поиск конкретных экспериментально наблюдаемых эффектов проявления свойств времени в нашем Мире. Представление о связи времени с причинностью пронизывает всю теорию Козырева. Это видно, в частности, из того, что все три постулата о свойствах времени содержат термины «причина» и «следствие». Именно убеждение ученого в наличии такой связи побудило его назвать свою теорию физических свойств времени причинной механикой. Н. А. Козырев так обосновывает введение первого постулата [1, с. 337]: «На необходимость этого постулата указывают трудности, связанные с развитием идеи Лейбница об определении направленности времени через причинные связи. Глубокие исследования Г. Рейхенбаха [5] и Дж. Уитроу [6] показывают, что нельзя строго, без тавтологии провести эту идею. Причинность говорит нам о существовании направленности у времени и о некоторых свойствах этой направленности, вместе с тем она не является сущностью этого явления, а только его результатом». Классическая механика Ньютона не делает различия между причиной и следствием (ибо в этой науке постулируется, что силы взаимодействия двух тел направлены вдоль одной прямой, равны между собой по модулю, противоположны по направлению и действуют в один момент времени). В этом состоит принципиальная ограниченность классической механики. Преодоление ее и является целью причинной механики. Обсуждаемый постулат утверждает, что время обладает как раз таким свойством, которое порождает различие между причиной и следствием. Можно отметить, что не совсем удачным в постулате I является использование терминов «направленность» и «ход времени» в качестве названий постулированного свойства времени в связи с тем, что первый из них уже имеет хождение в науке, причем со смыслом, отличающимся от приписываемого ему постулатом I, а второй термин используется далее в причинной механике не столько применительно к самому данному свойству времени, сколько к одной его количественной характеристике. Постулаты II и III не требуют пояснений, так как их содержание совершенно прозрачно и естественно. Оно согласуется со всем опытом естествознания, касающимся свойств причинности. И даже если в реальности все же выполняется условие dx = 0 или dt = 0, то можно ожидать, что и этот случай войдет в теорию в качестве соответствующего предельного варианта. В причинной механике, как отмечалось, вещество моделируется материальными точками. В рамках такой модели всякий процесс может быть представлен как последовательность отдельных причинно-следственных звеньев. При этом самое малое, элементарное, причинно-следственное звено состоит из двух материальных точек – точки-причины и точки-следствия, – которые согласно постулатам II и III разделены пространством и временем и между которыми уже нет никаких других материальных тел. Считается, что величины dx и dt, фигурирующие в постулатах II и III, относятся именно к такому элементарному причинно-следственному звену (причем они, вообще говоря, могут быть различными для разных звеньев). Заметим, что в причинной механике смысл величин dx и dt все же детально не прояснен. Это видно, например, из употребления по отношению к ним такого выражения: «эти символы означают предел бесконечно малых величин при условии, что они никогда не обращаются в нуль» [1, с. 338]. Однако данный недостаток не сказывается на последующем содержании теории, потому что эти величины не вычисляются в ней. Н. А. Козырев вводит в рассмотрение величину
которую называет ходом времени. При этом ученый принимает, что с2 есть псевдоскаляр, положительный в правой системе координат (в ранних статьях ученого величине c2 приписывался противоположный знак, но в более поздней работе принят именно этот знак, см. [1, с. 367]). Н. А. Козырев связывает псевдоскалярность c2 с наличием подобного свойства у величины Определение. Ходом времени c2 называется псевдоскаляр, положительный в правой системе координат и по абсолютной величине равный Ход времени c2 имеет размерность скорости и характеризует скорость перехода причины в следствие в элементарном причинно-следственном звене. Эта величина является основной количественной характеристикой в причинной механике. На основании того, что элементарное причинно-следственное звено не содержит между точкой-причиной и точкой-следствием никакого вещества, а только пространство и время, ученый заключает, что величина c2должна отражать свойства именно времени и пространства, а не конкретной физической системы или процесса. В связи с этим он делает предположение, что c2 представляет собой универсальную мировую константу, подобную, например, скорости света в вакууме. Данное положение не выделено автором причинной механики в качестве отдельного постулата, но по своей сути является именно таковым. Поэтому сформулируем его в виде четвертого постулата. Постулат IV.Ход времени c2 есть фундаментальная постоянная. С целью подчеркнуть аналогию между ходом времени и скоростью света – двумя мировыми константами, имеющими размерность скорости, – Н. А. Козырев использует для них схожие обозначения – соответственно с2 и с1. В отношении величины с2необходимо отметить следующее. Данная величина, как указывалось, характеризует скорость перехода причины в следствие в элементарном причинно-следственном звене. Однако величина с2 не есть наблюдаемая на макроскопическом уровне скорость реализации всей причинно-следственной цепи. Это связано с тем, что окончание одного элементарного причинно-следственного перехода и начало следующего могут быть разделены каким-то промежутком времени, требующимся, например, для перемещения точки-причины или точки-следствия из одного места пространства в другое. Здесь можно провести аналогию со взаимодействием молекул газа: между двумя последовательными взаимодействиями одной молекулы газа с другими протекает какое-то время, когда молекула движется свободно, без взаимодействий, причем это время может значительно превышать время осуществления отдельного межмолекулярного взаимодействия (особенно, в случае разреженного газа), поэтому скорости макроскопических процессов в газе, таких как распространение ударной волны и других, не связаны напрямую со скоростью осуществления отдельного межмолекулярного взаимодействия. Точно так же и наблюдаемая на макроскопическом уровне скорость реализации причинно-следственной цепи может быть не связана напрямую с величиной хода времени с2. Из этого ясно, что нет противоречия между утверждаемой постулатом IV одинаковостью значений с2 для любых процессов и различием макроскопических скоростей их протекания. Следующее положение причинной механики гласит, что в причинно-следственном звене при определенных условиях возникают силы, которые являются добавочными по отношению к силам, предсказываемым классической механикой. Считается, что эти добавочные силы обусловлены воздействием времени. Сформулируем настоящее положение в виде пятого постулата. Постулат V.Если в причинно-следственном звене имеет место относительное вращение точки-причины и точки-следствия, то в нем наряду с силами, учитываемыми классической механикой, действуют и определенные добавочные силы. При этом добавочные силы, приложенные к точке-причине и к точке-следствию, равны по модулю и противоположны по направлению, так что их главный вектор равен нулю. Вместе с тем, линии действия этих сил могут не совпадать, поэтому их главный момент может быть отличен от нуля. Для реального причинно-следственного звена, состоящего из макроскопических тела-причины и тела-следствия, при условиях, что: а) одно из тел вращается, а другое не вращается, б) вращающееся тело по форме близко к идеальному волчку (то есть вся его масса располагается примерно на одном расстоянии от оси вращения, а центр масс находится на этой оси), в) линейная скорость вращенияv (одинаковая по модулю для всех точек идеального волчка) удовлетворяет условию | v| << | с2 |, добавочные силы описываются выражениями
где КС, КП – равнодействующие добавочных сил соответственно для следствия и причины, приложенные в их центрах масс; v = | v|; F = | F|; F – учитываемая классической механикой сила взаимодействия причины и следствия; l – единичный псевдовектор, параллельный оси вращения и направленный в правой системе координат в сторону, откуда вращение кажется происходящим по ходу часовой стрелки. Из условия v << | с2 | и формул (3) следует, что |КС | = | КП | << F, поэтому силы КСи КП представляют собой малые добавки к «классической» силе F. Здесь мы несколько отошли от обозначений, использованных в [l]. В частности, обозначили добавочные силы буквой К по фамилии Козырева, а также в отличие от [l], где v – псевдоскаляр и l – (истинный) вектор, мы приняли, что v – (истинный) скаляр, l – псевдовектор. Важно, что добавочные силы, о которых идет речь в постулате V, не нарушают суммарный импульс причинно-следственного звена и вместе с тем могут изменять его момент импульса. (Это объясняется тем, что их главный вектор равен нулю, а главный момент может быть отличен от нуля.) Поскольку по отношению в целом ко всему причинно-следственному звену рассматриваемые добавочные силы являются внутренними, данное обстоятельство может приводить к нарушению закона сохранения момента импульса, хотя закон сохранения импульса остается справедливым. Обсудим эту ситуацию с позиции классической механики. Закон сохранения импульса и закон сохранения момента импульса являются одними из основных законов физики. Причем обычно считается, что к описанию поведения физических систем они применимы в равной степени. Однако, если обратиться к обоснованию этих законов, даваемому классической механикой, то можно увидеть, что они базируются на несколько различающихся допущениях. Так, закон сохранения импульса выводится непосредственно из законов Ньютона, закон сохранения момента импульса – из законов Ньютона и дополнительного допущения о том, что силы взаимодействия любых двух внутренних точек системы имеют одну линию действия [7, с. 137]. Из этого следует, что рассматриваемые законы только в том случае могут иметь одинаковую степень применимости к описанию природы, если указанное дополнительное допущение является таким же общим законом природы, как законы Ньютона. Между тем, в классической механике данное допущение не возводится в ранг фундаментального закона. Это говорит о том, что в классической механике заложена принципиальная возможность того, что при каких-то условиях указанное допущение и вместе с ним закон сохранения момента импульса могут нарушаться. Именно о таком случае идет речь в постулате V. Согласно данному постулату это нарушение может иметь место в причинно-следственных связях. Значимость постулата V определяется в первую очередь тем, что он открывает путь к экспериментальной проверке причинной механики. Проделав соответствующие опыты, Н. А. Козырев получил [l, с. 367, 382]:
где a – постоянная тонкой структуры (a » 1/137); с – скорость света в вакууме. Тот факт, что величина с2 оказалась близкой к произведению универсальных постоянных, служит определенным доводом в пользу справедливости постулата IV о ее фундаментальности. Постулат V впервые в физике устанавливает объективное отличие причин от следствий в простейших механических системах. Из (3) вытекает, что в случае причинно-следственного звена, содержащего вращающееся тело, можно узнать, является это тело причиной или следствием, по тому признаку, в какую именно сторону кажется происходящим его вращение при взгляде с той стороны, куда направлен вектор добавочной силы. Если вращение кажется происходящим по ходу часовой стрелки, то рассматриваемое тело является следствием, если — против хода часовой стрелки, то оно является причиной. Из этого видно, что в причинной механике различие причины и следствия связывается с различием правого и левого. Остановимся на тех положениях причинной механики, связанных с постулатом V, которые представляются недостаточно проработанными. Н. А. Козырев пишет [1, с. 343], что между силой действия и силой противодействия нет разрыва во времени, причем здесь подразумеваются и силы, описываемые формулами (3). Это означает, что причина и следствие воздействуют друг на друга одновременно. При этом остается неясным, как данное утверждение согласуется с постулатом III о наличии не равного нулю временного различия между причиной и следствием. В [I] при расчетах в качестве величины F, входящей в формулы (3), принимается вес того тела, для которого определяется значение добавочной силы. Однако непонятно, почему при этом не учитывается сила, действующая на тело со стороны подвеса. Опыты, описанные в [1], показали, что добавочные силы возникают в механической системе только при условии введения в нее некоторого причинного воздействия. (Последнее осуществлялось посредством механических вибраций, нагрева или пропускания электрического тока, причем источник воздействия помещался вблизи одного из концов системы, выполнявшего функцию причины, и воздействие естественным путем передавалось по системе к другому ее концу – следствию.) Таким образом, указанное воздействие играет определяющую роль в появлении эффекта. Между тем, никакие характеристики этого воздействия не входят в формулы (3), что вызывает удивление. Значение константы с2, описываемое выражением (4), вычислено в [1] с помощью не самих формул (3), а их видоизменений, отличающихся от (3) наличием в правых частях формул дополнительного множителя π (при отсутствии которого будет |с2| » 700 км/с). Однако доводы, приводимые в обоснование такого изменения формул [1, с. 366 – 367], не выглядят достаточно убедительными. Выскажем соображения относительно возможных способов исправления отмеченных недостатков. Первый из них – неучет временного различия между силами действия и противодействия – может быть исправлен, например, способом, изложенным в другой статье автора в настоящем издании. Следующие два отмеченные недостатка, которые касаются неучета силы, действующей на тело со стороны подвеса, и неучета причинного воздействия, вероятно, будут устранены, если при расчетах в качестве силы F принимать не силу тяжести, как это делается в [1], а непосредственно силу взаимодействия причины и следствия, как того требует постулат V. Тогда в случае причинно-следственного звена, у которого один элемент звена соединен с внешними телами, а другой удерживается силой F (как это имеет место в опытах Н. А. Козырева), данная сила будет включать в себя как силу, действующую со стороны подвеса, так и силу, связанную с причинным воздействием. Заметим, что если при этом сила F окажется пропорциональной массе тела, то соответствующие формулы будут отличаться от формул, учитывающих только вес тела, лишь числовым множителем. В отношении последнего из указанных выше недостатков – недостаточной обоснованности включения в формулы (3) дополнительного скалярного множителя – отметим следующее. Необходимость такого изменения формул может быть связана с целым рядом обстоятельств. Например, как мы только что отмечали, некоторый множитель может появиться в этих формулах вследствие использования при расчетах в качестве величины Fвеса тела. Кроме того, не исключено, что определенный множитель с самого начала должен был быть включен в формулы (3). Причин для этого несколько. Во-первых, величина с2 подставлена в формулы (3), очевидно, по соображениям размерности и на основании гипотезы о том, что источником появления добавочных сил служит свойство времени, определенное постулатами I – IV. Но, как легко видеть, в силу этих же причин с равным основанием может быть подставлена в формулы (3) вместо величины с2 любая величина kс2 с положительным безразмерным коэффициентом k, что даст в правых частях формул (3) дополнительный множитель k-1. Во-вторых, так как формулы (3) относятся не к микроскопическому причинно-следственному звену, состоящему из двух материальных точек, а к макроскопической системе, то было бы вполне закономерно, чтобы в них входил в качестве дополнительного множителя некий параметр, отражающий результат интегрирования при переходе от описания свойств материальных точек к описанию свойств макроскопической системы. В-третьих, некоторый множитель может войти в формулы (3) в том случае, если имеет место зависимость добавочных сил от относительной ориентации оси вращения и прямой причина–следствие (возможность существования такой зависимости в [1] не исследована, и поэтому не может быть априори исключена). Обратим внимание на то обстоятельство, что при наличии в правых частях формул (3) дополнительного множителя эксперимент по определению добавочных сил позволяет найти лишь отношение данного множителя и константы с2, а не каждую из этих величин в отдельности. Поэтому для их вычисления нужны дополнительные независимые основания. Такими основаниями могут служить результаты, которые получены в другой статье автора, помещенной в настоящей книге. Они свидетельствуют, что константа с2 действительно имеет значение, описываемое выражением (4). Из данного факта и результатов Н. А. Козырева по измерению добавочных сил вытекает, что дополнительный множитель равен π, то есть его значение и значение величины с2 совпадают с принятыми ученым. Таким образом, формулы (3) для добавочных сил должны быть преобразованы к виду
Отметим, что подобным же образом должны быть преобразованы аналогичные формулы в упомянутой выше работе автора. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
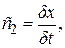 (1)
(1) . Однако доводы, приводимые в обоснование псевдоскалярности
. Однако доводы, приводимые в обоснование псевдоскалярности 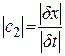 . (2)
. (2) (3)
(3)

 (5)
(5)