
|
|
коэффициентами и специальной правой частьюТеорема (о частном решении линейного неоднородного рекуррентного соотношения). Для любого линейного рекуррентного соотношения с постоянными коэффициентами f(n + k) = a1×f(n + k – 1) + …+ ak×f(n) + Tm(n)×ln, где Tm(x) – многочлен степени m, l Î С, существует решение вида nr×Sm(n)×ln , где Sm(x) – некоторый многочлен степени m, а r – кратность корня l в характеристическом уравнении xk – a1×xk–1 – … – ak–1×x – ak = 0 . В частности, если l не является корнем характеристического уравнения, то нужно считать r = 0. Доказательство. Подставим nr×(sm×nm+…+s1×n+s0)×ln в рекуррентное соотношение:
(здесь всегда можно считать m > r, используя, если необходимо, нулевые коэффициенты многочленов). В случае, когда l не является корнем характеристического многочлена, т.е. r = 0, система упрощается:
Видно, что система имеет верхнетреугольный вид с диагональными элементами c(l) ¹ 0, а потому имеет единственное решение. Если же l – это r-кратный корень характеристического многочлена c(x), то в силу леммы о соотношениях для r-кратного корня многочлена последняя группа уравнений системы тривиальна: все коэффициенты в ней нулевые. Действительно, эти коэффициенты имеют вид При этом
по упомянутой выше лемме. Более того, система снова верхнетреугольная. В самом деле, если j > u, токоэффициент при su в j-м уравнении первой группы (j £ r) равен
по лемме о соотношениях для r-кратного корня многочлена, т.к. u+r–j < r при j > u. При j = u коэффициент при su равен и отличен от нуля по той же лемме. Если же j > r, то коэффициенты могут быть ненулевыми только для значений u из диапазона j–r £ u £ m. При этом
по лемме о соотношениях для r-кратного корня многочлена, т.к. u+r–j < r при j > u. При j = u > r коэффициент при su равен Таким образом, в любом случае полученная система уравнений крамерова и имеет единственное решение. Теорема доказана. Эта теорема упрощает нахождение частных решений для линейных рекуррентных соотношений с постоянными коэффициентами, имеющими свободные члены специального рассмотренного в теореме вида. Пример. 1.Найти формулу общего члена решения рекуррентного соотношения f(n + 3) = f(n) + 1. Здесь c(x) = x3 – 1 имеет три простых корня l1 = 1, Таким образом, общее решение рассматриваемого неоднородного соотношения имеет вид c1×l1n + c2×l2n + c3×l3n + 2. Найти формулу общего члена решения рекуррентного соотношения f(n + 1) = f(n) + n2 – 1. Здесь c(l) = l – 1 имеет единственный корень l = 1, так что общее решение однородного соотношения j(n, c) = c. Частное решение неоднородного соотношения будем искать в виде n·(s2×n2+s1×n+s0)×1n, т.к. свободный член рассматриваемого соотношения имеет вид 1n×T2(n), где T2(x) = x2 – 1. Подставляя это выражение в исходное соотношение, получим s2×(n + 1)3+s1×(n + 1)2+s0×(n + 1) = s2×n3 + s1×n2 + s0×n + n2 – 1, т.е. 3×s2×n2+(3×s2 + 2×s1)×n + s2 + s1+s0 = n2 – 1, откуда w(n) = с + ( Некоторые примеры применения Производящих функций
I. Вычисление частичных сумм последовательностей. Пусть задана последовательность {un} Имеем s(x) = s0 + s1×x + s2×x2 +… = u0 + (u0+u1)×x + (u0 + u1 + u2)×x2 +… = = u0 + u1×x + u2×x2 + … + u0×x + (u0 + u1)×x2 +… = u(x) + s(x)×x. Отсюда получаем (1 – x)×s(x) = u(x), и окончательно s(x) = Знание производящей функции, как было показано ранее, позволяет находить формулы для членов последовательностей. Таким образом, открывается путь для задания формулами частичных сумм последовательностей. Пример. Пусть un = n (n Î N0). Тогда u(x) = Поэтому s(x) = (1 – y) –r = 1+r×y+ то полученная формула записывается в виде ряда Таким образом, sn = 2. Доказательство некоторых тождеств. Рассмотрим известную формулу бинома Ньютона:
а с другой – справедливо равенство
Сравнивая коэффициенты при одинаковых степенях x в полученных формулах, приходим к соотношению Таким образом, производя алгебраические действия с производящими функциями, можно получать нетривиальные соотношения для членов изучаемых последовательностей. Л И Т Е Р А Т У Р А 1.Акимов О.Е. Дискретная математика: логика, группы, графы. – М.: Лаборатория Базовых Знаний, 2001.
2.Асеев. Дискретная математика: Учеб. пособие – Ростов н / Д.: Феникс, 2003.
3.Виленкин Н.Я. Элементы комбинаторики. – М.: Наука, 1969.
4.Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по дискретной математике. Учеб. пособие. – М.: Физматлит, 2004.
5.Журавлёв Ю.И. и др. Сборник задач по дискретному анализу. Комбинаторика. Элементы алгебры и логики. Теория графов. – М.: МФТИ-рио, 2004.
6.Зыков А.А. Основы теории графов: Учебник. – М.: Вузовская книга, 2004.
7.Матросов В.Л., Стеценко В.А. Лекции по дискретной математике. – М.: МПГУ, 1997.
8.Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2002.
9.Редькин Н.П. Дискретная математика. – СПб.: Издательство “Лань”, 2006.
10.Холл М. Комбинаторика. – М.: Мир, 1970.
11.Яблонский С.В. Введение в дискретную математику. – М.: Высш. шк., 2006.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|




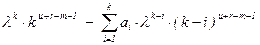 , где u = m+j–r (j = 1, … , r).
, где u = m+j–r (j = 1, … , r).



 и отличен от нуля по той же лемме.
и отличен от нуля по той же лемме. , а свободный член соотношения представим в виде 1 = l1n×T0(x), где T0(x) = 1. Таким образом, общее решение однородного соотношения записывается в виде c1×l1n + c2×l2n + c3×l3n, а частное решение неоднородного соотношения – в виде c×n×l1n = c×n. Подставляя это выражение в исходное соотношение, получаем соотношение с×(n+3) = c×n + 1, откуда находим c =
, а свободный член соотношения представим в виде 1 = l1n×T0(x), где T0(x) = 1. Таким образом, общее решение однородного соотношения записывается в виде c1×l1n + c2×l2n + c3×l3n, а частное решение неоднородного соотношения – в виде c×n×l1n = c×n. Подставляя это выражение в исходное соотношение, получаем соотношение с×(n+3) = c×n + 1, откуда находим c =  .
. .
. , а значит, s2 =
, а значит, s2 = 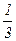 , s1 = –
, s1 = –  , s0 = –
, s0 = –  . Таким образом, общее решение рассматриваемого неоднородного соотношения имеет вид
. Таким образом, общее решение рассматриваемого неоднородного соотношения имеет вид с производящей функцией u(x) =
с производящей функцией u(x) =  . Найдём производящую функцию s(x) последовательности {sn}
. Найдём производящую функцию s(x) последовательности {sn}  .
. =
=  .
. . Если учесть, что
. Если учесть, что ·y2 + … =
·y2 + … =  ,
, .
. , т.е. 1+2+…+n =
, т.е. 1+2+…+n =  .
. . Сумму в правой части можно рассматривать как производящую функцию последовательности
. Сумму в правой части можно рассматривать как производящую функцию последовательности  , где
, где  для i £ n, и
для i £ n, и  при i > n. Тогда, с одной стороны,
при i > n. Тогда, с одной стороны, ,
,
 , в котором, как и выше, считается, что
, в котором, как и выше, считается, что