
|
|
Постоянными коэффициентами
Рассуждения, аналогичные использованным, можно применить для нахождения общего решения произвольного линейного однородного рекуррентного соотношения с постоянными коэффициентами f(n + k) = a1×f(n + k – 1) + … + ak×f(n). Теорема. Следующие условия для последовательности {un} комплексных чисел эквивалентны: (1) последовательность {un} f(n + k) = a1×f(n + k – 1) +… + ak×f(n). (2) un = Доказательство. (1) Þ (2) Если un+k = a1×un+k–1 +…+ ak×un (n Î N0), то умножая каждое из этих равенств на xn и складывая, получим: uk×x0 + uk+1×x1+… = a1×( uk–1×x0 + uk×x1+…)+…+ak×(u0×x0+u1×x1+ …) Û Û u(x)×(1–a1×x–a2×x2– … –ak–1×xk–1–ak×xk) = = (u0+u1×x+…+uk–1×xk–1) – a1×x×(u0+u1×x+…+uk–2×xk–2)– … – ak–1×xk–1×u0 . В правой части этого равенства стоит многочлен P(x) = (u0+u1×x+…+uk–1×xk–1) – a1×x×(u0+u1×x+…+uk–2×xk–2)– … – ak–1×xk–1×u0 степени не выше k–1, так что u(x) = (2) Þ (3) Пусть u(x) = xk – a1×xk–1 – … – ak–1×x – ak = (x – l1) где l1 , … , ls – попарно различные корни кратностей r1 , … , rs . Ясно, что 1 – a1×x – … – ak×xk = = = (1 – l1×x) Поэтому производящую функцию u(x) можно представить в виде u(x) = разложения в сумму простых дробей, где bij Î C (1 £ i £ s, 1 £ j £ ri). Здесь важно учитывать, что степень числителя P(x) меньше степени знаменателя. Воспользовавшись разложениями в ряд
u(x) = По определению производящей функции, коэффициент при степенях переменной x равен соответствующему члену последовательности. Значит, (3) Þ (1) Пусть теперь Нужно доказать, что такая последовательность будет решением рассматриваемого линейного однородного рекуррентного соотношения с постоянными коэффициентами. Ввиду линейной структуры решений этого соотношения достаточно проверить, что решениями будут все произведения вида kj×lik , где 0 £ j < ri . Это значит, что выполнены следующие соотношения: (n+k)j×ln+k = a1×(n+k–1)j×ln+k–1+…+ak×nj×ln , l = li , n Î N0 . Если l = 0 – корень многочлена c(x) = xk – a1×xk–1 –…– ak–1×x – ak , то ak = 0, и соотношения выполняются. Они будут выполнены и в случае j = 0, т.к. lk = a1×lk–1 + …+ ak–1×l + ak . В случае j ³ 1 воспользуемся формулой бинома Ньютона
(n+k)j×ln+k = a1×(n+k–1)j×ln+k–1+…+ak×nj×ln Û Û (n+k)j×lk = a1×(n+k–1)j×lk–1+…+ak–1×(n+1)j×l+ak×nj Û Û Докажем, что совпадают коэффициенты при всех степенях n, т.е. lk = a1×lk–1 + … + ak–1×l + ak (для nj), Û lk–1×ki = a1×lk–2×(k–1)i+…+ak–2×l×2i+ak–1 (для nj–i , i > 0). Это следует из приводимой ниже леммы. Теорема доказана. Лемма (соотношения для r-кратного корня многочлена). Если l – корень кратности r > 0 многочлена f(x) = xk – a1×xk–1 – … – ak–1×x – ak , то справедливы соотношения lk = a1×lk–1 + … + ak–1×l + ak , lk–1×ki = a1×lk–2×(k–1)i+…+ak–2×l×2i+ak–1 (1 £ i < r). При этом lk–1×kr ¹ a1×lk–2×(k–1)r+…+ak–2×l×2r+ak–1 . Доказательство. Проведём индукцию по степени многочлена. Для многочлена первой степени нужно доказать только первое из соотношений, которое следует и в общем случае из условия леммы (l – корень многочлена). При этом очевидно, что указанное в формулировке леммы неравенство тоже выполнено. Столь же просто рассматривается и случай k = 2. Предположим, что лемма доказана для многочленов степени меньше k и докажем её для многочлена степени k. Поскольку l – корень кратности r–1 для производной многочлена f¢(x) = k×xk–1 – a1×(k–1)×xk–2 – … – ak–2×2×x – ak–1 степени k–1, то запишем соответствующие соотношения для многочлена
(1 £ i < r – 1), которые можно записать так: lk–1×k = a1×lk–2×(k–1)+…+ak–2×l×2+ak–1 , lk–2×(k–1)i×k = a1×lk–3×(k–2)i×(k–1)+a2×lk–4×(k–3)i×(k–2)+…+ak–3×l×3×2i+ak–2×2 (1 £ i < r–1). Первое из этих равенств даёт искомое соотношение при i = 1 для исходного многочлена, а из второй группы равенств получаем: lk–1×k2–lk–1×k = a1×lk–2×(k–2)×(k–1)+a2×lk–3×(k–3)×(k–2)+…+ak–3×l2×3×2+ak–2×2×l , lk–1×k2 = (a1×lk–2×(k–2)×(k–1)+a2×lk–3×(k–3)×(k–2)+…+ak–3×l2×3×2+ak–2×2×l)+ +(a1×lk–2×(k–1)+a2×lk–3×(k–2)+…+ak–3×l2×3+ak–2×l×2+ak–1) = = a1×lk–2×(k–1)2+ a2×lk–3×(k–2)2+…+ ak–3×l2×32+ ak–2×l×22+ak–1 . Это – доказываемое соотношение для исходного многочлена при i = 2. Если эти соотношения уже доказаны при i = 1, 2, … , s < r и s+1 < r, то s < r+1 и можно воспользоваться s-м из доказанных соотношений: lk–1×(k–1)s×k = a1×lk–2×(k–2)s×(k–1)+a2×lk–3×(k–3)s×(k–2)+…+ak–3×l2×3×2s+ak–2×2×l Û
Если предположить, что lk–1×kr = a1×lk–2×(k–1)r+…+ak–2×l×2r+ak–1 , то приведённые выше преобразования, пройденные в обратном порядке, приведут к соотношению lk–1×(k–1)r–1×k=a1×lk–2×(k–2)r–1×(k–1)+a2×lk–3×(k–3)r–1×(k–2)+…+ak–3×l2×3×2r–1+ak–2×2×l Û
Лемма доказана. Эта теорема даёт алгоритм нахождения общего решения линейного рекуррентного соотношения с постоянными коэффициентами

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 является решением линейного однородного рекуррентного соотношения с постоянными коэффициентами
является решением линейного однородного рекуррентного соотношения с постоянными коэффициентами , где l1 , … , ls – различные корни характеристического уравнения c(l) = 0 кратностей r1 , … , rs соответственно, где c(l) = lk – a1×lk–1 –…– ak–1×l – ak – характеристический многочлен, (это значит, что lk – a1×lk–1 – … – ak–1×l – ak = (l – l1)
, где l1 , … , ls – различные корни характеристического уравнения c(l) = 0 кратностей r1 , … , rs соответственно, где c(l) = lk – a1×lk–1 –…– ak–1×l – ak – характеристический многочлен, (это значит, что lk – a1×lk–1 – … – ak–1×l – ak = (l – l1)  ×…×(l – ls)
×…×(l – ls)  ), а Pi(x) – некоторый многочлен, степень которого меньше соответствующей кратности ri (1 £ i £ s).
), а Pi(x) – некоторый многочлен, степень которого меньше соответствующей кратности ri (1 £ i £ s).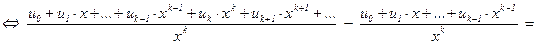

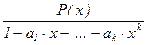 , что и требовалось.
, что и требовалось. , где P(x) – многочлен степени не выше k–1. Разложим многочлен xk – a1×xk–1 – … – ak–1×x – ak в произведение линейных множителей над алгебраически замкнутым полем C:
, где P(x) – многочлен степени не выше k–1. Разложим многочлен xk – a1×xk–1 – … – ak–1×x – ak в произведение линейных множителей над алгебраически замкнутым полем C: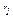 ×…×(x – ls)
×…×(x – ls) 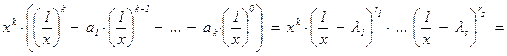
 × … ×(1 – ls×x)
× … ×(1 – ls×x)  .
.
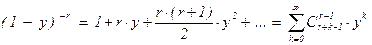 , получим
, получим
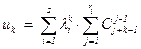 (k Î N0). При этом участвующую здесь сумму
(k Î N0). При этом участвующую здесь сумму  можно рассматривать как многочлен от k, степень каждого из выделенных слагаемых в котором не превосходит j–1 , в целом степень многочлена не превосходит ri – 1. Обозначая этот многочлен через Pi(x), получим:
можно рассматривать как многочлен от k, степень каждого из выделенных слагаемых в котором не превосходит j–1 , в целом степень многочлена не превосходит ri – 1. Обозначая этот многочлен через Pi(x), получим:  , что и требовалось.
, что и требовалось. .
. :
: .
. Û
Û :
:
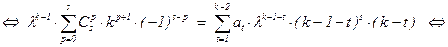


 Это противоречит предположению индукции для многочлена
Это противоречит предположению индукции для многочлена  .
.