
|
|
Примеры решения простейших комбинаторных задачПодытожим сведения об изученных комбинаторных объектах и их числовых характеристиках в следующей таблице:
Задача 0.На флагштоке поднимается сигнал, содержащий 1, 2 или 3 различных флага из стандартного набора, содержащего 3 флага. Сколько различных сигналов получится (порядок флагов учитывается) ? Ответ: 15. Решение. Из одного флага – 3 сигнала, из двух и из трёх флагов – по 6 сигналов. Далее – принцип сложения. Задача 1.В магазине есть 7 разных видов чашек и 5 различных видов блюдец. Сколькими способами можно купить чашку с блюдцем ? Ответ: 35-ю способами. Решение. Типичная задача на принцип умножения. Представим себе, что из города A в город B ведут 7 дорог, на каждой из которых продают разные виды чашек. А из города B в город C ведут 5 дорог, на каждой из которых продают один вид блюдец. Таким образом, чайный набор покупается при проезде из A в C, что можно сделать 35-ю способами. Задача 2.Монета бросается 10 раз и получается набор длины 10 из выпавших результатов: орёл или решка. Сколько различных наборов с четырьмя орлами получится ? Ответ: Задача 3.Сколько слов (произвольных последовательностей) длины 1000 можно составить из букв русского алфавита ? Ответ: 331000 . Решение. В русском алфавите 33 буквы. Так что Задача 4.Простейшая молекула белка, как утверждают учёные-биологи, представляет собой последовательность длины 50 из основных 20-ти аминокислот. Оцените, сколько лет потребуется, чтобы перебрать все возможные комбинации таких последовательностей, если в каждом кубическом миллиметре шарового слоя Земли высоты 10 км. за одну секунду осуществляется независимый перебор 1000000 вариантов ? Ответ: более 10 21лет.
Объём шара V = = £ Далее, 1 км3 = 109 м3 = 109·106 см3 = 1015·103 мм3 . Значит, объём рассматриваемого шарового слоя меньше 1029 мм3. Даже, если перебор комбинаций будет вестись в 1029 мм3, то одному из этих кубических миллиметров нужно перебрать не менее В одном году менее 60·60·24·366 < 100·100·100·1000 = 109 секунд. Значит, понадобится более А как же возраст Вселенной, оцениваемый учёными-астрофизиками в 20 миллиардов лет (20·109 = 2·1010 лет) ?! Могла ли случайная эволюция за это время создать не только простейшую молекулу белка, но и гораздо более сложные структуры ? Например, геном человека, как утверждают те же учёные-биологи, является последовательностью из » 25000 генов, а каждый ген сам обладает сложной структурой ! Думайте сами, решайте сами… Задача 5.Каждую клетку таблицы 3´3 можно раскрасить в 3 цвета. Сколькими способами можно раскрасить таблицу, чтобы в каждой строке и в каждом столбце встречались все три цвета ? Ответ: 12. Решение. Для определённости обозначим цвета клеток средней строки буквами б, с, к. Тогда нетрудно понять, что возможны только следующие два варианта раскраски таблицы:
Учитывая, что допускаются произвольные перестановки цветов, т.е. вместо порядка (б, с, к) можно рассматривать произвольный другой порядок – перестановку этих букв, получим 2×3 ! = 12 раскрасок. Задача 6.Сколько можно сшить трёхцветных флагов из полосок материи шести цветов, если флаги с одинаковыми цветами, но различными их расположениями считать разными ? Ответ: Решение. Типичная задача на размещения шести элементов по трём местам. А если не учитывать расположение полос ? Тогда Задача 7.В стране 30 городов, каждые два из которых соединены авиалиниями. Сколько всего авиалиний ? Ответ: Решение. Авиалиния определяется своими концами, т.е. произвольно выбранными двумя городами из 30. Число этих сочетаний равно Задача 8.Игральный кубик бросают шесть раз. Сколько последовательностей из шести результатов бросаний содержат хотя бы одну шестёрку ? Ответ: 21031. Решение. Проще вычислить, в скольких случаях совсем нет шестёрки. Это произойдёт в 56 случаях из общего числа 66 случаев. Таким образом, хотя бы одна шестёрка выпадает в 66 – 56 = (62)3 – (52)3 = (62–52)×(64+62×52+54) = = 11×((62+52)2–62×52) = 11×(61+30)×(61–30) = 11×91×31 = 91×341 = 90×341+341= = 30690 + 341= 31031 случаях. Задача 9.Сколько четырёхзначных чисел можно составить из цифр 0, 3, 5, 8 (цифры не повторяются) ? Ответ: 18. Решение. P4 – P3 = 4 ! – 3 ! = 18 (учесть, что 0 не может быть старшей цифрой). Замечание.Если цифры могут повторяться, то получится 3·43 = 192 числа. Если исключать число 0 = 0000, то останется 191 число. Задача 10.У математика 7 книг, а у поэта – 9. Сколькими способами можно обменять две математические книги на четыре поэтических ? Ответ: 15876. Решение. Правило умножения: Задача 11.Сколько различных (в том числе и бессмысленных) слов можно составить из букв слов ТИГР, ПАРА. Ответ: 24, 12. Решение.Для слова ТИГР, в котором нет одинаковых букв, ответ 4! = 24. Для слова ПАРА – Для слова ПАРАЛЛЕЛОГРАММ, в котором три буквы А и Л, по две буквы Р и М аналогично получим Задача 12.Сколько всего результатов бросания трёх одинаковых игральных костей ? Ответ: 56. Решение.Сочетания с повторениями: результат бросания представляет собой набор Задача 13.Карточная колода из 52 карт раздаётся 4-м игрокам: вначале 13 карт первому, потом – 13 карт второму, и т.д. В скольких случаях каждому из игроков будет роздано по тузу ? Ответ: 134× Решение.Рассматриваем колоду как слово из 52 различных букв. Если один из тузов, например, туз червей (Ч), попал в первые 13 букв, то он может оказаться на любой позиции с 1-й по 13-ю, а на остальных позициях могут участвовать все буквы, кроме тузов, без повторений, т.е. Для второго игрока и туза бубён (Б) ситуация аналогична, только уже нельзя использовать карты первого игрока: количество вариантов 13× По принципу умножения получаем 134× Задача 14.Сколько существует автобусных билетов с шестизначными номерами, в которых участвуют только цифры 3, 5, 7, и сумма цифр которых делится на 3 ? Ответ: 213. Решение. Общее число автобусных билетов с цифрами 3, 5, 7 подсчитать легко: это просто
Всего получается 1+2·20+2·1+30+2·15+90+20 = 213 билетов. Задача 15.Доказать равенство Решение. По формуле бинома Ньютона имеем Отсюда Задача 16.Вычислить сумму “арифмо-геометрической” прогрессии 1 + 2×q + 3×q2 + … + (n+1)×qn . Ответ: Решение. Дифференцируя формулу суммы геометрической прогрессии 1 + x + … + xn+1 = получим 1+2×x+…+(n+1)×xn = Для правильной записи ответа нужно учесть случай q = 1. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Î As
Î As


 Î An, as ¹ at при s ¹ t
Î An, as ¹ at при s ¹ t

 }, as ¹ at при s ¹ t
}, as ¹ at при s ¹ t

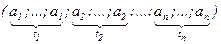

 = 1260.
= 1260. .
. Решение. Всего последовательностей длины 50 из 20 аминокислот будет 2050 = 250·1050 .
Решение. Всего последовательностей длины 50 из 20 аминокислот будет 2050 = 250·1050 . ·p·R3 , поэтому объём шарового слоя высоты h вычисляется так: Vh =
·p·R3 , поэтому объём шарового слоя высоты h вычисляется так: Vh =  = 250·1021
= 250·1021 
 = 1027 лет. Учитывая, что в каждую секунду производится перебор 106 вариантов, время перебора сокращается до 10 21 лет.
= 1027 лет. Учитывая, что в каждую секунду производится перебор 106 вариантов, время перебора сокращается до 10 21 лет. = 120.
= 120. = 20.
= 20. = 435.
= 435. = 435 .
= 435 . = 21×756 = 15876.
= 21×756 = 15876. = 12: ПАРА, ПРАА, ПААР, АПРА, АРПА, ААРП, АПАР, ААПР, АРАП, РПАА, РАПА, РААП. Здесь две буквы А можно менять местами, поэтому и делим на количество перестановок на двух символах.
= 12: ПАРА, ПРАА, ПААР, АПРА, АРПА, ААРП, АПАР, ААПР, АРАП, РПАА, РАПА, РААП. Здесь две буквы А можно менять местами, поэтому и делим на количество перестановок на двух символах. = 605404800.
= 605404800. , где
, где  . Поэтому количество результатов равно
. Поэтому количество результатов равно  .
. ×12!×4! .
×12!×4! . . Всего вариантов (по принципу сложения) 13×
. Всего вариантов (по принципу сложения) 13×  . Для третьего и туза пик (П) – 13×
. Для третьего и туза пик (П) – 13×  , а для четвёртого и трефового туза (Т) – 13×
, а для четвёртого и трефового туза (Т) – 13×  = 13×12! .
= 13×12! . ×
×  ×
×  ×12! . В этих вычислениях был фиксирован порядок тузов: (Ч, Б, П, Т). Ясно, что возможны любые перестановки. Так что ответ: 134×
×12! . В этих вычислениях был фиксирован порядок тузов: (Ч, Б, П, Т). Ясно, что возможны любые перестановки. Так что ответ: 134×  = 36. Какие из номеров билетов делятся на 3 ? Те, сумма цифр которых делится на 3. Цифру 3 при этом, очевидно, можно не учитывать. Если в номере участвуют k пятёрок и m семёрок, то их сумма k×5+m×7 = k×(5+7)+(m–k)×7 делится на 3 тогда и только тогда, когда делится на 3 разность m–k. Можно перечислить все варианты:
= 36. Какие из номеров билетов делятся на 3 ? Те, сумма цифр которых делится на 3. Цифру 3 при этом, очевидно, можно не учитывать. Если в номере участвуют k пятёрок и m семёрок, то их сумма k×5+m×7 = k×(5+7)+(m–k)×7 делится на 3 тогда и только тогда, когда делится на 3 разность m–k. Можно перечислить все варианты: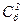 = 30
= 30
 = 15×6
= 15×6
 .
.
 . С другой стороны, как было отмечено выше,
. С другой стороны, как было отмечено выше,  . Сравнивая коэффициенты при одинаковых степенях x, получим требуемое равенство.
. Сравнивая коэффициенты при одинаковых степенях x, получим требуемое равенство. при q = 1,
при q = 1,  при q ¹ 1.
при q ¹ 1. (x ¹ 1),
(x ¹ 1), .
.