
|
|
Размещения и перестановки с повторениямиНачнём с примеров: 1.Сколько существует слов русского алфавита длины 7 ? Под словом понимается любая последовательность букв. Эта задача легко решается по принципу умножения: первую букву слова можно написать 33-мя способами, вторую – тоже 33-мя, и т.д. Всего получается 33×33×33×33×33×33×33 = 337 слов. 2.Сколько существует различных шестизначных номеров автобусных билетов из цифр 0, 3, 9 ? А сколько существует шестизначных чисел из тех же цифр ? Ясно, что искомое число автобусных билетов равно 36 = 729 (на каждую из шести позиций номера можно поставить любую из трёх цифр 0, 3, 9). Шестизначных чисел будет гораздо меньше, т.к. незначащие нули в них не допускаются. Поэтому первая (старшая) цифра выбирается из двух, а остальные пять – из трёх. Всего получится 2·35 = 486. Если A = {a1 , … , an } – конечное множество из n элементов, то размещением n элементов с повторениями по k местам называется любой упорядоченный набор (b1 ; … ; bk) элементов множества A, в котором могут встречаться одинаковые компоненты. Обозначим через Примеры: 1. любое размещение без повторений является размещением с повторениями. Если s > n, то ни одного размещения без повторений n элементов по s местам не существует, хотя размещений с повторениями много: (a1 ; a1 ; … ; a1), (a1 ; a2 ; … ; a2), и т.д. 2. Перечислим все размещения с повторениями длины 2 для множества из трёх элементов A = {1, 2, 3}: (1; 1), (1; 2), (1; 3), (2; 1), (2; 2), (2; 3), (3; 1), (3; 2), (3; 3). Поэтому Так же как для размещений без повторений легко понять, что после выбора первого элемента, осуществимого n способами в размещении с повторениями (b1 ; b2 ; … ; bk) остаётся незаполненным “хвост” (b2 ; … ; bk), представляющий собой размещение с повторениями из элементов множества A по k – 1 местам. Количество способов заполнить этот “хвост” равно Рассмотрим задачу: сколько слов (возможно, бессмысленных) можно получить перестановкой букв в слове АБРАКАДАБРА ? Отличие этой задачи от аналогичной задачи для слова КОЛУН, решённой в предыдущем параграфе, заключается в том, что не всякая перестановка одиннадцати букв слова приводит к различным словам. Это происходит потому, что в слове АБРАКАДАБРА есть одинаковые буквы. Рассмотрим вспомогательное слово А1Б1Р1А2КА3ДА4Б2Р2А5 , все буквы которого различны. Тогда из него можно составить 11 ! различных слов путём перестановки букв. Однако, если в этих словах снова заменить введённые фиктивные буквы A1 , A2 , A3 , A4 , A5 на А, а буквы Б1 и Б2 – на Б и Р1 , Р2 – на Р, то некоторые слова станут одинаковыми. Какие это слова ? Нетрудно понять, что два слова станут одинаковыми тогда и только тогда, когда фиктивные буквы Xi (для каждой группы X Î {A, Б, Р}) в рассматриваемых словах лишь переставлены местами. Таких перестановок будет 5 ! для клонов буквы А, 2 ! – для клонов буквы Б, и 2 ! – для клонов буквы Р. Таким образом, из одного слова, составленного из букв слова АБРАКАДАБРА можно составить 5 !×2 !×2 ! различных слов из букв-клонов. Поэтому общее количество искомых слов равно Обобщая ситуацию, приходим к следующему определению: перестановка с повторениями элементов множества А = {a1 , … , an} кратностей k1 , … , kn и длины k = k1 + … + kn – это упорядоченный набор Каждая перестановка с повторениями является, конечно, размещением n элементов множества А по k местам с повторениями. Примеры: 1. Перечислим все перестановки с повторениями из двух элементов кратностей 1, 2. Вначале ставим на первое место a1 и перечисляем все перестановки из элементов a1 , a2 кратностей 0, 2, т.е. все перестановки из одного элемента a2 кратности 2. Такая перестановка единственна: (a2 ; a2). Приписывая к ней a1 на первом месте, получим (a1 ; a2 ; a2). Теперь ставим a2 на первое место и перечисляем все перестановки из элементов a1 , a2 кратностей 1, 1 : (a1 ; a2), (a2 ; a1). Приписывая к ним a2 на первом месте, получим ещё две перестановки (a2 ; a1 ; a2), (a2 ; a2 ; a1). Итак, всего есть 3 перестановки с повторениями из двух элементов кратностей 1, 2 : (a1 ; a2 ; a2), (a2 ; a1 ; a2), (a2 ; a2 ; a1). 2. Перечислим все перестановки с повторениями из двух элементов кратностей 2, 2. Аналогично предыдущему получаем: (a1 ; a1 ; a2 ; a2), (a1 ; a2 ; a1 ; a2), (a1 ; a2 ; a2 ; a1), (a2 ; a1 ; a1 ; a2), (a2 ; a1 ; a2 ; a1), (a2 ; a2 ; a1 ; a1). Каково количество Сколько всего перестановок n элементов с повторениями длины k ? Очевидно, что это число равно количеству всех размещений n элементов по k местам, т.е. nk . В этом можно убедиться окольным, но полезным путём. Для этого нужно заметить, что при вычислении степени (a1 + … + an)k получается сумма произведений
Если подставить a1 = … = an = 1, то получим nk = Пример: = x3 + y3 + z3 + 3·x2·y + 3·x2·z + 3·x·y2 + 3·x·z2 + 3·y2·z + 3·y·z2 + 6·x·y·z. Здесь коэффициент

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 количество размещений n элементов с повторениями длины k.
количество размещений n элементов с повторениями длины k. .
. . Таким образом, получается рекуррентная формула
. Таким образом, получается рекуррентная формула  , причём, очевидно, что
, причём, очевидно, что  . Поэтому
. Поэтому  .
.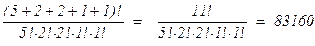 .
.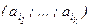 длины k, в котором элемент ai встречается ki раз (1 £ i £ n). Количество таких перестановок обозначим
длины k, в котором элемент ai встречается ki раз (1 £ i £ n). Количество таких перестановок обозначим  .
. , заменив каждый элемент ai на ki элементов-клонов
, заменив каждый элемент ai на ki элементов-клонов  (1 £ i £ n) в соответствии с его кратностью. Теперь можно рассмотреть все перестановки элементов этого множества из k = k1 + … + kn элементов. Их, как известно, будет k ! = (k1 + … + kn) ! . Если в любой такой перестановке заменить элементы
(1 £ i £ n) в соответствии с его кратностью. Теперь можно рассмотреть все перестановки элементов этого множества из k = k1 + … + kn элементов. Их, как известно, будет k ! = (k1 + … + kn) ! . Если в любой такой перестановке заменить элементы  произвольным образом переставлены символы
произвольным образом переставлены символы  .
.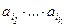 , которые можно отождествлять с перестановками с повторениями
, которые можно отождествлять с перестановками с повторениями  . После приведения подобных при этом мономе возникнет коэффициент
. После приведения подобных при этом мономе возникнет коэффициент  . Таким образом, доказана важная формула, обобщающая формулу бинома Ньютона:
. Таким образом, доказана важная формула, обобщающая формулу бинома Ньютона: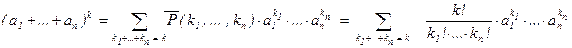 .
. – общее число всех перестановок n элементов с повторениями длины k.
– общее число всех перестановок n элементов с повторениями длины k.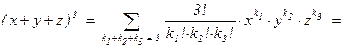
 вычислен для каждого решения (k1 ; k2 ; k3) уравнения k1 + k2 + k3 = 3: (3; 0; 0), (0; 3; 0), (0; 0; 3), (2; 1; 0), (2; 0; 1), (1; 2; 0), (1; 0; 2), (0; 2; 1), (0; 1; 2), (1; 1; 1).
вычислен для каждого решения (k1 ; k2 ; k3) уравнения k1 + k2 + k3 = 3: (3; 0; 0), (0; 3; 0), (0; 0; 3), (2; 1; 0), (2; 0; 1), (1; 2; 0), (1; 0; 2), (0; 2; 1), (0; 1; 2), (1; 1; 1).