
|
|
Подмножества конечных множеств и сочетанияЕсли A = {a0 , … , an–1 } – конечное множество из n элементов, то символом В(А) будем обозначать булеан множества A, т.е. множество всех подмножеств множества А. Для того, чтобы поближе познакомиться с булеаном, рассмотрим следующую задачу: как перечислить все элементы булеана В(А) конечного n-элементного множества А = {a0 , … , an–1} ? Для бесконечных множеств булеан, очевидно, тоже бесконечен и поэтому менее обозрим, нежели в конечном случае. Каждому подмножеству X Í A сопоставим n-значное двоичное число e(X) = en–1×2n–1+…+e0×20 = ( Примеры. 1.Если A = {a0 , a1 , a2} и X = {a0 , a2}, то e(X) = 1012 = 5, а если X = {a1 }, то e(X) = 0102 = 2. Вообще, можно составить полный список подмножеств множества А:
Видно, что значения e(X) пробегают всё множество {0, 1, 2, 3, 4, 5, 6, 7}, и В(А) состоит из восьми элементов. 2. Перечислить все подмножества четырёхэлементного множества A = {a0 , a1 , a2 , a3 }. Будем перечислять подмножества, выписывая соответствующие им наборы из нулей и единиц:
В общем случае наименьшее значение e(X), очевидно, равно 0…02 = 0 для множества X = Æ, а наибольшее значение равно 1…12 = 1×2n–1+…+1×20 = = 2n–1+…+ 2+1 = Инъективность: " X1 , X2 Î В(А) e(X1) = e(X2) ® X1 = X2 . Действительно, если Сюръективность: " n Î {0, 1, … , 2n–1} $ X Î В(А) e(X) = n. Действительно, по любому двоичному числу n = Теорема (о нумерации подмножеств конечного множества). (1) Существует биективное соответствие f : В(A) ® {0, … , 2n – 1} между всеми подмножествами конечного множества A = {a1 , … , an} из n элементов и интервалом целых чисел 0 .. 2n – 1. (2) Существует биективное соответствие f : Вm(A) ® Bm Í {0, … , 2n–1} между всеми m-элементными подмножествами конечного множества A = {a1 , … , an} из n элементов и всеми целыми числами диапазона 0 .. 2n – 1, имеющими в своей двоичной записи ровно m единиц (и n–m нулей). Следствие (о количественаборов из нулей и единиц длины n).Количество всевозможных наборов из нулей и единиц длины n равно 2n . Доказательство следствия очевидно, т.к. количество всевозможных наборов из нулей и единиц длины n равно количеству чисел от 0 до 2n – 1, т.е. 2n. Следствие доказано. Следствие (о количестве подмножеств n-элементного множества). Любое n-элементное множество содержит 2n подмножеств. Доказательство. Построенное выше взаимно однозначное отображение e : В({a0 , … , an–1}) ® {0, 1, … , 2n – 1} показывает, что количество элементов в В({a0 , … , an–1}) равно количеству элементов в {0, 1, … , 2n – 1}, т.е. 2n .
Если A = {a1 , … , an } – конечное множество из n элементов, то сочетанием (или выборкой) из n объектов a1 , … , an по k штук (сочетанием из n по k) называется произвольное k-элементное подмножество Теорема (о перечислении сочетаний). Существует взаимно однозначное соответствие между всеми сочетаниями из n элементов конечного множества A = {a1 , … , an} по m и всеми целыми числами диапазона 0 .. 2n – 1, имеющими в своей двоичной записи ровно m единиц (и n–m нулей). Следствие (о количестве всех сочетаний из n элементов). Общее количество всех сочетаний из n элементов по всем m (0 £ m £ n) равно 2n . Имея алгоритм перечисления всех подмножеств множества A, легко понять, как получить алгоритм перечисления сочетаний. Нужно среди всех наборов из нулей и единиц длины n отобрать наборы ровно с k единицами и построить по ним соответствующие k-элементные множества. Пример: Выписать все сочетания из четырёх элементов по двадля множества A = {1, 2, 3, 4}. Среди всех наборов из нулей и единиц, перечисленных выше, отбираем только те, которые содержат 2 единицы и 4 нуля:
Вычислим теперь количество сочетаний (1+a1×x)×(1+a2×x)×…×(1+an×x) = = 1 + (a1+…+ak)×x+(a1×a2+a1×a3+…+ak–1×ak)×x2 + … … +(a1×…×an–1+…+a2×…×an)×xn–1 + a1×…×an×xn . Если теперь подставить a1 = a2 = … = an = 1, то, с одной стороны, при xk получится количество сочетаний из n по k, а с другой, – мы придём к формуле бинома Ньютона: (1 + x)n = 1+n×x+ Следовательно, Из формулы бинома Ньютона немедленно получаются следующие полезные равенства: Кроме того, Отметим ещё раз связь между размещениями, сочетаниями и перестановками. Сочетание Сочетания с повторениями Рассмотрим задачу: сколько всего букетов можно составить из семи роз, пяти фиалок и трёх тюльпанов, если каждый букет состоит из одной розы, двух фиалок и двух тюльпанов (порядок цветов в букете не важен) ? Это – простая задача на сочетания и принцип умножения: Другая задача: сколько букетов, содержащих 3 цветка, можно составить из роз, фиалок и тюльпанов (цветов достаточное количество и порядок цветков в букете не существенен) ? Здесь букет можно мыслить как набор роз 3: такой набор единственный (р; р; р); роз 2: таких наборов два (р; р; ф), (р; р; т); роз 1: таких наборов три (р; ф; ф), (р; ф; т); (р; т; т); роз 0: таких наборов четыре (ф; ф; ф), (ф; ф; т), (ф; т; т); (т ; т; т). Всего, таким образом, получится 10 букетов. Хотя результат и получен, но не вполне понятно, как решать эту задачу для букетов из большего количества k цветов в букете: даже для k = 5 перечислить все букеты затруднительно ! Поэтому надо задуматься об общем методе решения задачи. Пусть Таким образом, найден более перспективный способ подсчёта букетов, основанный на рекуррентном соотношении Если A = {a1 , … , an } – конечное множество из n элементов, то сочетанием n элементов с повторениями называется любой упорядоченный набор вида Перечислить все сочетания с повторениями длины k можно рекурсивно. Ясно, что существует ровно n различных сочетаний с повторениями длины 1: (a1), … , (an). Если уже умеем перечислять все сочетания с повторениями, но от меньшего чем n количества элементов, то вначале выпишем единственное сочетание кратности k по a1 : Пример: Перечислим все сочетания с повторениями длины 4 для трёхэлементного множества A = {1, 2, 3}. (1; 1; 1; 1), (1; 1; 1; 2), (1; 1; 1; 3), (1; 1; 2; 2), (1; 1; 2; 3), (1; 1; 3; 3), (1; 2; 2; 2), (1; 2; 2; 3), (1; 2; 3; 3); (1; 3; 3; 3), (2; 2; 2; 2), (2; 2; 2; 3), (2; 2; 3; 3); (2; 3; 3; 3), (3; 3; 3; 3). Таким образом, Проанализировав приведённый выше алгоритм перечисления всех сочетаний с повторениями длины k, получим рекуррентную формулу: Сразу не видно, как получить формулу для s = 1: Ясно, что s = 2: Имеем
s = 3: Имеем Возникает гипотеза о том, что
Это следует из основного равенства
– верно. Другой способ доказательства формулы {a1 , … , an ; b1 , … , В этом сочетании каждому ai кратности ki > 0 соответствует группа элементов Пример: Сочетаниям с повторениями длины 3 из множества A = {1, 2} сопоставим следующие сочетания элементов множества Это соответствие взаимно однозначно и в общем случае: инъективность: если {a1 , … , an ; b1 , … , то из правила построения этого сочетания сразу следует, что s1–1 = p1–1 = t1–1, т.е. s1 = t1 , s2–1 = p2–1 = t2–1, т.е. s2 = t2 , … , sn–1 = pn–1 = tn–1, т.е. sn = tn , так что рассматриваемые сочетания с повторениями совпадают. сюръективность: по любому сочетанию {a1 , … , an ; b1 , … , однозначно восстанавливается его прообраз. Действительно, если a1 не участвует в сочетании, то его кратность в сочетании с повторениями равна 0.Если же a1 участвует в сочетании, то выделяем максимальный отрезок подряд участвующих в этом сочетании элементов b1 , … , Примеры: 1.Сочетанию {a1 , a3 , b1 , b2} из пяти элементов по четыре соответствует сочетание с повторениями (a1 ; a1 ; a1; a3) длины 4 элементов множества A = {a1 , a2 , a3}. 2. Сочетанию {a2 , a3 , b1 , b3 } из пяти элементов по четыре соответствует сочетание с повторениями (a2 ; a2 ; a3 ; a3 ) длины 4 элементов множества A = {a1 , a2 , a3}. 3. Сочетанию {a2 , b1 , b2 , b3 } из пяти элементов по четыре соответствует сочетание с повторениями (a2 ; a2 ; a2; a2) длины 4 элементов множества A = {a1 , a2 , a3}.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 )2 с цифрами ei Î {0, 1} (0 £ i £ n–1), однозначно определяющее это подмножество. Вместо двоичного числа в этих рассуждениях можно рассматривать и просто набор e(X) = (en–1 ; … ; e0) длины n из нулей и единиц. Итак, положим
)2 с цифрами ei Î {0, 1} (0 £ i £ n–1), однозначно определяющее это подмножество. Вместо двоичного числа в этих рассуждениях можно рассматривать и просто набор e(X) = (en–1 ; … ; e0) длины n из нулей и единиц. Итак, положим  (0 £ i £ n–1). Кстати, именно такой способ интерпретации множеств реализуется в некоторых языках программирования.
(0 £ i £ n–1). Кстати, именно такой способ интерпретации множеств реализуется в некоторых языках программирования. = 2n – 1 при X = {a0 , … , an–1 } = A.Таким образом построена функция e : В(A) ® {0, 1, … , 2n – 1}. Докажем, что она биективна.
= 2n – 1 при X = {a0 , … , an–1 } = A.Таким образом построена функция e : В(A) ® {0, 1, … , 2n – 1}. Докажем, что она биективна. = e(X1) = e(X2) =
= e(X1) = e(X2) =  , то e0 = d0 , … , en–1 = dn–1 . Поэтому для любого элемента ai Î A верно ai Î X1 Û ei = 1 Û di = 1 Û ai Î X2 и значит, множества X1 и X2 состоят из одних элементов, т.е. равны.
, то e0 = d0 , … , en–1 = dn–1 . Поэтому для любого элемента ai Î A верно ai Î X1 Û ei = 1 Û di = 1 Û ai Î X2 и значит, множества X1 и X2 состоят из одних элементов, т.е. равны.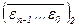 образуем множество X по правилу ai Î X Û ei = 1 (0 £ i £ n–1). Ясно, что e(X) =
образуем множество X по правилу ai Î X Û ei = 1 (0 £ i £ n–1). Ясно, что e(X) =  Í A. Количество всех сочетаний из n по k обозначается
Í A. Количество всех сочетаний из n по k обозначается  .
.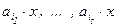 , где i1 < i2 < … < is . Таким образом, коэффициент при таком мономе соответствует выбору сочетания {
, где i1 < i2 < … < is . Таким образом, коэффициент при таком мономе соответствует выбору сочетания {  }, причём это соответствие взаимно однозначно, т.к. множество {
}, причём это соответствие взаимно однозначно, т.к. множество {  } однозначно определяется элементами
} однозначно определяется элементами  , а количество таких слагаемых в точности равно количеству сочетаний из n по s.
, а количество таких слагаемых в точности равно количеству сочетаний из n по s.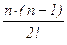 ×x2 + … +
×x2 + … +  ×xk + … +n×xn–1+xn .
×xk + … +n×xn–1+xn . – биномиальный коэффициент, который равен количеству сочетаний из n элементов по k.
– биномиальный коэффициент, который равен количеству сочетаний из n элементов по k.
 – известные свойства биномиальных коэффициентов.
– известные свойства биномиальных коэффициентов. из n по k отличается от размещения без повторений
из n по k отличается от размещения без повторений  тем, что для сочетания не важен порядок элементов. Поэтому, произвольным образом переставляя элементы размещения, будем получать одно и то же сочетание. Количество перестановок рассматриваемого сочетания равно k ! , так что одному сочетанию соответствует k ! размещений. Поэтому
тем, что для сочетания не важен порядок элементов. Поэтому, произвольным образом переставляя элементы размещения, будем получать одно и то же сочетание. Количество перестановок рассматриваемого сочетания равно k ! , так что одному сочетанию соответствует k ! размещений. Поэтому  .
. = = 7×10×3 = 210.
= = 7×10×3 = 210. , в которых р – розы, ф – фиалки, т – тюльпаны и k1 + k2 + k3 = 3. Поэтому возможны следующие случаи:
, в которых р – розы, ф – фиалки, т – тюльпаны и k1 + k2 + k3 = 3. Поэтому возможны следующие случаи: – количество букетов, составляемых из k видов цветов, каждый из которых содержит j цветов. Тогда, нужно найти
– количество букетов, составляемых из k видов цветов, каждый из которых содержит j цветов. Тогда, нужно найти  , и согласно схеме перечисления по количеству роз
, и согласно схеме перечисления по количеству роз  . Здесь
. Здесь  – учитывает единственный набор (р; р; р),
– учитывает единственный набор (р; р; р),  – количество “хвостов” (ф) и (т) при двух розах,
– количество “хвостов” (ф) и (т) при двух розах,  – количество “хвостов” (ф; ф), (ф; т); (т; т) при одной розе, и
– количество “хвостов” (ф; ф), (ф; т); (т; т) при одной розе, и  – количество букетов (ф; ф; ф), (ф; ф; т), (ф; т; т); (т; т; т) при отсутствии роз. Ясно, что
– количество букетов (ф; ф; ф), (ф; ф; т), (ф; т; т); (т; т; т) при отсутствии роз. Ясно, что  . Аналогично
. Аналогично  . Так что теперь получим
. Так что теперь получим  .
. .
.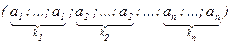 , где ki Î N0 . Если ki = 0, то это значит, что в наборе элемент ai отсутствует. Числа ki , … , kn называются кратностями элементов a1 , … , an в сочетании с повторениями. Число сочетаний с повторениями длины k = k1 + … + kn будем обозначать через
, где ki Î N0 . Если ki = 0, то это значит, что в наборе элемент ai отсутствует. Числа ki , … , kn называются кратностями элементов a1 , … , an в сочетании с повторениями. Число сочетаний с повторениями длины k = k1 + … + kn будем обозначать через 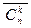 .
. , затем перечислим все сочетания с повторениями кратности k – 1 по a1 (и кратности 1 по элементам множества A1 = A \ {a1}= {a2 , … , an }) – их
, затем перечислим все сочетания с повторениями кратности k – 1 по a1 (и кратности 1 по элементам множества A1 = A \ {a1}= {a2 , … , an }) – их  . Затем – кратности k – 2 по a1 (и кратности 2 по элементам множества A1) – их
. Затем – кратности k – 2 по a1 (и кратности 2 по элементам множества A1) – их  , и т.д., пока не перечислим все сочетания кратности 1 по a1 (и кратности k – 1 по элементам множества A1 ) – их
, и т.д., пока не перечислим все сочетания кратности 1 по a1 (и кратности k – 1 по элементам множества A1 ) – их  , и наконец, все сочетания кратности 0 по a1 (и кратности k по элементам множества A1 ) – их
, и наконец, все сочетания кратности 0 по a1 (и кратности k по элементам множества A1 ) – их  .
.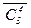 = 15. Попутно получаем
= 15. Попутно получаем  = 5,
= 5,  = 4,
= 4, 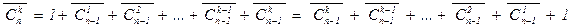 .
. .
.
 .
.

 . Для её обоснования достаточно проверить выполнение рекуррентного соотношения:
. Для её обоснования достаточно проверить выполнение рекуррентного соотношения: .
. для биномиальных коэффициентов:
для биномиальных коэффициентов:
 обычное сочетание n+k–1 элементов множества
обычное сочетание n+k–1 элементов множества 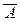 = {a1 , … , an , b1 , … , bk–1} по k :
= {a1 , … , an , b1 , … , bk–1} по k :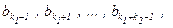 … ,
… ,  }.
}.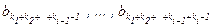 количество которых ki – 1. Если кратность элемента равна 0, то ни он сам, ни соответствующая ему группа во множестве не участвуют. Общее количество элементов в построенном сочетании будет 1+(k1–1)+1+(k2–1)+…+1+(kn–1) = k.
количество которых ki – 1. Если кратность элемента равна 0, то ни он сам, ни соответствующая ему группа во множестве не участвуют. Общее количество элементов в построенном сочетании будет 1+(k1–1)+1+(k2–1)+…+1+(kn–1) = k.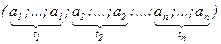 привели к одному и тому же сочетанию
привели к одному и тому же сочетанию , … ,
, … ,  },
}, … ,
… , 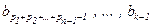 }
} и записываем в искомом сочетании с повторениями элемент a1 с кратностью s1 . При этом ситуация, когда элемент b1 не входит в сочетание возникнуть не может, т.к. в противном случае элементов из множества {b1 , … , bk–1} будет участвовать меньше k–1, а поскольку рассматриваемое сочетание имеет n+k–1 элемент, то количество участвующих в нём элементов из множества A должно быть больше n, что невозможно. Точно так же процесс построения искомого сочетания с повторениями происходит и далее.
и записываем в искомом сочетании с повторениями элемент a1 с кратностью s1 . При этом ситуация, когда элемент b1 не входит в сочетание возникнуть не может, т.к. в противном случае элементов из множества {b1 , … , bk–1} будет участвовать меньше k–1, а поскольку рассматриваемое сочетание имеет n+k–1 элемент, то количество участвующих в нём элементов из множества A должно быть больше n, что невозможно. Точно так же процесс построения искомого сочетания с повторениями происходит и далее.