
|
|
Метод производящих функций для нахожденияОбщего решения линейного однородного рекуррентного Соотношения второго порядка Продемонстрируем общий метод решения линейных однородных соотношений с постоянными коэффициентами на примере соотношения второго порядка. Использованный для нахождения формулы членов общего решения этого рекуррентного соотношения метод производящих функций будет в дальнейшем применён и в общем случае. Для последовательности {un} Идея применения производящих функций для решения рекуррентных соотношений состоит в том, чтобы найти в явном виде производящую функцию решения соотношения, разложить её в ряд и получить формулы для коэффициентов этого ряда, которые совпадают с членами искомой последовательности. Эти вычисления выполняются с помощью простейших алгебраических операций над рядами: сложения и умножения на двучлены. Рассмотрим линейное однородное рекуррентное соотношение с постоянными коэффициентами f(n + 2) = a1×f(n + 1) + a2×f(n), где a2 ¹ 0 (иначе соотношение будет первого порядка). Любое его решение {un} u2 = a1×u1 + a2×u0 | ´ x0 u3 = a1×u2 + a2×u1 | ´ x1 . . . ui+2 = a1×ui+1 + a2×ui | ´ xi . . . Умножая эти равенства на xi и складывая, получим u2×x0 + u3×x1 + … + ui+2×xi + … = a1×(u1×x0 + u2×x1 + … + ui+1×xi + … ) + + a2×(u0×x0 + u1×x1 + … + ui×xi + … ), которое эквивалентно системе написанных выше равенств: эти равенства немедленно получаются, если приравнять коэффициенты при одинаковых степенях переменной x в этих рядах. Далее, u2×x0 + u3×x1+u4×x2 + … = a1×( u1×x0 + u2×x1+u3×x2+…)+a2×(u0×x0+u1×x1+ …) Û Û u(x)×(1 – a1×x – a2×x2) = u0 + u1×x – u0×a1×x, т.е. Рассмотрим характеристическое уравнение c(x) = x2 – a1×x – a2 = 0, которое всегда имеет корни где U0 = u0 , U1 = u1 – a1×u0 . Оказывается, что эту дробь можно разложить в сумму элементарных дробей. Под этим понимается разложение вида В этом легко убедиться непосредственно, найдя числа A и B. В первом случае, умножив на общий знаменатель (1 – l1×x)×(1 – l2×x), получим равенство U0 + U1×x = A×(1 – l2×x) + B×(1 – l1×x). Приравнивая коэффициенты при одинаковых степенях x, приходим к системе уравнений Во втором случае кратного корня аналогично получаем: U0 + U1×x = A×(1 – l×x) + B Û Здесь l ¹ 0, поскольку иначе a2 = l1×l2 = 0 – противоречие. Рассмотрим теперь два случая: 1. l1 ¹ l2 . Тогда
Û (1 + y + y2 + … ) – y – y2 – y3 – … = 1, что верно. Таким образом, в случае различных корней получим
Вспоминая определение производящей функции, получаем un = A×l1n + B×l2n , где A и B – некоторые комплексные постоянные. 2. l1 = l = l2 . Тогда
Таким образом,
Поэтому un = ((A+B) + B×n)×ln , для некоторых констант A, B Î C . Проверим теперь, что последовательности un = c1×l1n + c2×l2n (в случае l1 ¹ l2) и un = (c1 + с2×n)×ln (для случая l1 = l = l2) с произвольными постоянными c1 , c2 Î C будут решениями линейного однородного рекуррентного соотношения f(n+2) = a1×f(n+1) + a2×f(n) второго порядка. В первом случае: f(n+2) – a1×f(n+1) + a2×f(n) = = c1×l1n+2 + c2×l2n+2 – a1×(c1×l1n+1 + c2×l2n+1) – a2×( c1×l1n + c2×l2n) = = c1×l1n×(l12 – a1×l1 – a2) + c2×l2n×(l22 – a1×l2 – a2) = 0 + 0 = 0, т.к. l1 и l2 – корни уравнения l2 – a1×l – a2 . Во втором случае f(n+2) – a1×f(n+1) + a2×f(n) = = (с1 + с2×(n+2))×ln+2 – a1×(с1 + с2×(n+1)) ln+1 – a2×(с1 + с2×n) ln = = c1×ln×(l2 – a1×l – a2) + c2×ln×((n+2)×l2 – a1×(n+1)×l – a2×n) = = c1×ln×0 + c2×ln×[n×(l2 – a1×l – a2) +2×l2 – a1×l] = c2×ln×[n×0 + 0] = 0, т.к. l2 – a1×l – a2 = 0 и x2 – a1×x – a2 = (x – l)×(x – l), т.е. a1 = 2×l . Итак, доказана Теорема (об общем решении линейного однородного рекуррентного соотношения с постоянными коэффициентами). Следующие условия для последовательности {un} комплексных чисел эквивалентны: (1) последовательность {un} f(n + 2) = a1×f(n + 1) + a2×f(n). (2) если характеристическое уравнение c(l) = 0, где c(l) = l2 – a1×l – a2 , имеет два различных корня l1 и l2 , то un = l1n×c1 + l2n×c2 (c1 , c2 Î C); если характеристическое уравнение c(l) = 0, где c(l) = l2 – a1×l – a2 , имеет два совпавших корня l1 = l = l2 , то un = ln×(c1 + c2×n) (c1 , c2 Î C). Эта теорема даёт метод нахождения общего решения произвольного однородного линейного рекуррентного соотношения с постоянными коэффициентами: 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 введём в рассмотрение формальный степенной ряд u(x) =
введём в рассмотрение формальный степенной ряд u(x) =  , называемый производящей функцией последовательности {un}
, называемый производящей функцией последовательности {un}  . Ясно, что этот ряд хранит всю информацию об исходной последовательности.
. Ясно, что этот ряд хранит всю информацию об исходной последовательности. удовлетворяет соотношениям:
удовлетворяет соотношениям: Û u(x) – u0 – u1×x = a1×x×(u(x) – u0) +a2×x2×u(x) Û
Û u(x) – u0 – u1×x = a1×x×(u(x) – u0) +a2×x2×u(x) Û .
. в поле комплексных чисел C . При этом c(x) = x2 – a1×x – a2 = (x – l1)×(x – l2). Теперь 1 – a1×x – a2×x2 = =
в поле комплексных чисел C . При этом c(x) = x2 – a1×x – a2 = (x – l1)×(x – l2). Теперь 1 – a1×x – a2×x2 = =  = (1–l1×x)×(1 – l2×x), так что
= (1–l1×x)×(1 – l2×x), так что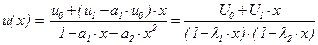 ,
, в случае l1 ¹ l2 и разложение
в случае l1 ¹ l2 и разложение  при l1 = l = l2 .
при l1 = l = l2 . относительно A и B, из которой находим
относительно A и B, из которой находим  .
. .
.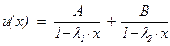 , и для разложения в ряд можно применить легко доказываемую формулу
, и для разложения в ряд можно применить легко доказываемую формулу  = 1 + y + y2 + … :
= 1 + y + y2 + … : .
. . Для получения разложения в ряд второй дроби продифференцируем разложение
. Для получения разложения в ряд второй дроби продифференцируем разложение  .
.