
|
|
Сводка некоторых результатов1.
Числа Каталана. Рассмотрим следующую задачу, решённую ещё Леонардом Эйлером: каково число разбиений выпуклого (n+2)-угольника (n ³ 1) на треугольники непересекающимися диагоналями ? Диагональю считается любой отрезок, соединяющий две вершины многоугольника, а разбиение – это произвольное множество треугольников, не имеющих общих внутренних точек, покрывающее весь многоугольник. Например, выбрав произвольную вершину многоугольника, можно из неё провести все диагонали в другие вершины и получить одно из возможных разбиений. Обозначим искомое число разбиений через Kn – это и есть числа Каталана. Легко понять, что K1 = 1, K2 = 2, K3 = 5. В общем случае перенумеруем вершины (n+2)-угольника числами 1, … , i, … , n+2 и рассмотрим любой треугольник с вершинами 1, i, n+2 (2 £ i £ n+1). Любое разбиение исходного (n+2)-угольника, содержащее этот треугольник, получается комбинированием любого разбиения на треугольники i-угольника M, рассматриваемого треугольника и произвольного разбиения на треугольники (n+3–i)-угольника N (смотри рисунок выше). В случае, когда i = 3 или i = n, многоугольники M или N превращаются в треугольники, а в случае i = 2 или i = n+1 – они вырождаются. Для применимости предыдущих рассмотрений удобно считать, что K0 = 1.Каждое разбиение исходного (n+2)-угольника на треугольники обязательно содержит некоторый треугольник с вершинами 1, i, n+2, поэтому получаем следующую рекуррентную формулу: Для нахождения общей формулы можно воспользоваться методом производящих функций. Если получим
Следовательно, Числа Каталана возникают в разнообразных комбинаторных задачах. Например, можно показать, что количество следующих объектов равно Kn : - число всех последовательностей (a1 ; … ; a2·n) длины 2×n, в которых ai Î {–1, 1} (1 £ i £ 2·n), - число всех последовательностей, состоящих из n открывающих и n закрывающих скобок, в которых для любой позиции количество закрывающих скобок слева не превосходит количества открывающих скобок слева; - число всех (2´n)-матриц с компонентами 1, 2, … , 2·n, расположенными в порядке возрастания в каждой строке и каждом столбце; - число всех монотонных функций f : {1, … , n} ® {1, … , n} со свойством f(i) £ i при любом i Î {1, … , n}; - число бинарных деревьев (см. Конспект лекций по дискретной математике, § 6 главы III). Конечно, можно легко найти обобщение чисел Каталана: например числа Числа Стирлинга первого рода. Рассмотрим произвольную подстановку на n символах 1, … , n : Алгоритм такого разложения прост и может быть проиллюстрирован на примере подстановки s = (1, 2, 5, 6) –1·s = (6, 5, 2, 1)· которая имеет меньше перемещаемых символов, чем s. Повторяя с ней ту же процедуру, находим нетривиальный цикл 3 ® 4 ® 7 ® 3 и рассматриваем подстановку (3, 4, 7) –1·s1 = (7, 4, 3)· тождественная подстановка. Таким образом, (3, 4, 7) –1·(1, 2, 5, 6) –1·s = e, и значит, s = (1, 2, 5, 6)·(3, 4, 7) – произведение двух нетривиальных циклов. Та же подстановка может быть записана в виде произведения трёх циклов: s = (1, 2, 5, 6)·(3, 4, 7)·(8), включая тривиальный цикл (8). Тождественная подстановка e на n символах раскладывается в произведение n тривиальных циклов: e = (1)·(2)· … ·(n). Это единственная подстановка на n символах, раскладывающаяся в произведение n циклов. Каноническим разложением подстановки называется такое её разложение в произведение независимых циклов, что в каждом цикле наименьший элемент стоит на первом месте и эти наименьшие элементы не убывают в порядке следования циклов. Например, разложение (1, 2, 5, 6)·(3, 4, 7)·(8) – каноническое, а следующие разложения той же подстановки (2, 5, 6, 1)·(3, 4, 7)·(8), (1, 2, 5, 6)·(4, 7, 3)·(8), (8)·(1, 2, 5, 6)·(3, 4, 7) – не канонические. Если в каноническом разложении стереть скобки, то получится перестановка чисел 1, … , n. Например, для рассмотренной подстановки s получится перестановка p = (1, 2, 5, 6, 3, 4, 7, 8). Оказывается, что сопоставление s a p является биективным. Число Стирлинга первого рода обозначается через Приведём таблицу начальных значений величин
Какой рекуррентной формулой связаны числа Стирлинга первого рода ? Если подстановка s на (n+1)-м символе разложена в произведение m независимых циклов s = с1·…·cm , то ровно один из этих циклов содержит n+1, а произведение остальных циклов даёт подстановку на n символах, раскладывающуюся в произведение (m – 1)-го цикла. Если цикл с n+1 тривиален, то подстановка s получена из подстановки на n символах c (m–1)-м циклом дописывание в конце тривиального цикла (n+1). Таких подстановок которая вместе с приведёнными начальными условиями позволяет вычислять числа Стирлинга первого рода. Некоторые важные свойства этих чисел будут приведены ниже в разделе 4 этого параграфа. 2. Числа Стирлинга второго рода. Число Стирлинга
Вывести рекуррентную формулу для чисел Стирлинга второго рода несложно. Если есть какое-либо разбиение m-элементное разбиение (n+1)-элементного множества, то ровно одному из множеств разбиения принадлежит n + 1. Если это множество одноэлементно, то рассматриваемое разбиение получено добавлением к (m–1)-элементному разбиению n-элементного множества ещё одного множества {n+1}. Так можно получить В итоге получаем рекуррентную формулу Она вместе с приведёнными начальными условиями позволяет вычислять числа Стирлинга первого рода. Некоторые важные свойства этих чисел будут приведены ниже в разделе 4 этого параграфа. 3. Некоторые важные формулы-свойства рассмотренных чисел. Приведём некоторые полезные свойства биномиальных коэффициентов и чисел Стирлинга первого и второго родов. Всюду обозначение r относится к действительным числам, а n и m – к натуральным или целым. Использование действительных чисел оправдано тем, что выражения Конечно, приведённые формулы не претендуют на полноту, их пополнение – непрерывная забота каждого математика. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 .
. , то
, то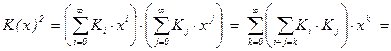
 . Значит, K(x) удовлетворяет уравнению x·K(x)2 – K(x) + 1 = 0, решением которого является функция
. Значит, K(x) удовлетворяет уравнению x·K(x)2 – K(x) + 1 = 0, решением которого является функция  . Воспользовавшись разложением в ряд
. Воспользовавшись разложением в ряд ,
,

 . Ясно, что знак + не подходит ввиду неотрицательности степеней переменной в K(x). Значит, сравнивая коэффициенты, получим формулу для чисел Каталана
. Ясно, что знак + не подходит ввиду неотрицательности степеней переменной в K(x). Значит, сравнивая коэффициенты, получим формулу для чисел Каталана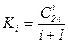 (i Î N0).
(i Î N0). ;
; , где q – заданное натуральное число (i Î N0).
, где q – заданное натуральное число (i Î N0). . Как известно, она может быть разложена (однозначно с точностью до порядка) в произведение независимых циклов, включая тривиальные:
. Как известно, она может быть разложена (однозначно с точностью до порядка) в произведение независимых циклов, включая тривиальные:  .
. : находим нетривиальный цикл 1 ® 2 ® 5 ® 6 ® 1 и рассматриваем подстановку
: находим нетривиальный цикл 1 ® 2 ® 5 ® 6 ® 1 и рассматриваем подстановку =
=  = s1 ,
= s1 , = e –
= e – равно числу подстановок на n символах, разлагающихся в k циклов, включая тривиальные. При этом по определению полагают
равно числу подстановок на n символах, разлагающихся в k циклов, включая тривиальные. При этом по определению полагают  = 1,
= 1,  = 0 (k > 0),
= 0 (k > 0),  = 0 (n > 0),
= 0 (n > 0),  = 1,
= 1,  = 0 (k > 1).
= 0 (k > 1).









 . Если же цикл с n+1 не тривиален, то он получен из некоторого цикла для подстановок на n символов с помощью вставки числа n+1 не на первое место. Таким образом, в этом случае s получается из подстановки на n символах с m циклами путём вставки в некоторый из циклов элемента n+1 не на первое место. Учитывая отмеченное выше биективное соответствие разложений с перестановками, получим
. Если же цикл с n+1 не тривиален, то он получен из некоторого цикла для подстановок на n символов с помощью вставки числа n+1 не на первое место. Таким образом, в этом случае s получается из подстановки на n символах с m циклами путём вставки в некоторый из циклов элемента n+1 не на первое место. Учитывая отмеченное выше биективное соответствие разложений с перестановками, получим  возможностей конструирования подстановок s в этом случае. Итак, получена рекуррентная формула
возможностей конструирования подстановок s в этом случае. Итак, получена рекуррентная формула ,
,  второго рода – это количество разбиений n-элементного множества в объединение m непересекающихся подмножеств (порядок подмножеств не учитывается). При этом по определению полагают
второго рода – это количество разбиений n-элементного множества в объединение m непересекающихся подмножеств (порядок подмножеств не учитывается). При этом по определению полагают  = 1,
= 1,  = 0,
= 0,  = 0. Приведём таблицу начальных значений этих величин:
= 0. Приведём таблицу начальных значений этих величин:









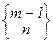 разбиение. Если же множество разбиения, содержащее n + 1, содержит более одного элемента, то рассматриваемое разбиение получено добавлением n + 1, к одному из m-элементных разбиений n-элементного множества. Таких возможностей конструирования будет m·
разбиение. Если же множество разбиения, содержащее n + 1, содержит более одного элемента, то рассматриваемое разбиение получено добавлением n + 1, к одному из m-элементных разбиений n-элементного множества. Таких возможностей конструирования будет m·  .
.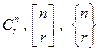 являются многочленами от r. Через dm, n обозначается символ Кронекера : эта величина равна 1, если m = n, и равна 0 в противном случае.
являются многочленами от r. Через dm, n обозначается символ Кронекера : эта величина равна 1, если m = n, и равна 0 в противном случае.