
|
|
Метод ранговой корреляцииВ практике параметрического ценообразования применение индексного и балльного методов предполагает широкое использование экспертных заключений для оценки степени значимости изменения параметров. В качестве экспертов могут привлекаться специалисты, хорошо знающие рынок изучаемого товара, а также покупатели. В данном случае в качестве инструмента прогнозирования может быть использован метод ранговой корреляции, а согласованность мнений экспертов может быть оценена коэффициентом конкордации. Коэффициент конкордации
где
Если среди рангов, данных одним экспертом, есть равные, то коэффициент конкордации рассчитывается (формула 6.21):
Коэффициент конкордации позволяет судить о степени согласованности мнений экспертов. Если Традиционно коэффициент конкордации менее 0,75 свидетельствует о недостаточной согласованности мнений экспертной группы, чтобы по результатам опроса экспертом можно было построить достоверный прогноз. Низкая согласованность мнений покупателей, выступающих в роли экспертов, может служить сигналом для сегментирования рынка и дифференцированного ценообразования. Для обоснования дифференциации и сегментирования можно использовать результаты метода ранговой корреляции по отдельным группам покупателей и локальные коэффициенты конкордации. Последовательность расчетов методом ранговой конкордации выглядит следующим образом: 1) получение индивидуальных экспертных оценок относительно важности, значимости, приоритетности, оцениваемых параметров; оценки экспертов даются в виде весовых коэффициентов, которые могут принимать значение от 0 до 1, сумма коэффициентов, данных одним экспертом, должна равняться единице; 2) ранжирование оценок важности, данных экспертами; каждая оценка, данная i-ым экспертом, выражается рангом 3) расчет суммы рангов по каждому направлению
4) расчет среднего значения суммы рангов по всем направлениям
где
5) расчет отклонения суммы рангов по
6) расчет показателя, характеризующего равные ранги (формула 6.25):
где 7) расчет коэффициента конкордации; выводы о согласованности мнений экспертов; 8) анализ значимости исследуемых параметров; параметр с наименьшей суммой рангов имеет наибольшее значение; средний коэффициент весомости определяется как отношение величины обратной сумме рангов к их сумме. Метод парных сравнений Согласно данному методу, эксперту предлагается сравнить параметры (объекты) попарно, используя шкалу отношений. Эксперт не дает количественных оценок преимуществ одного параметра перед другим или степени значимости параметров, а использует понятия больше, меньше, равно (лучше, хуже, неразличимо). Степень предпочтения параметров заранее считается неизвестной, она определяется в результате обработки полученных оценок. Результаты оценивания фиксируются в виде квадратной матрицы смежности парных сравнений в виде знаков: >, если <, если =, если Обозначения: Далее строится квадратная матрица (формула 6.26):
Здесь
Далее в расчет вводится понятие «итерированная сила» порядка
Итерированная сила объекта
В начале расчета принимается итерированная сила Исходную матрицу Далее этот процесс продолжается с учетом полученной итерированной силы предыдущей итерации. Практическую ценность в данном методе представляет так называемая нормированная итерационная сила

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 – показывает степень согласованности мнений экспертов по важности каждого из оцениваемых параметров. Рассчитывается (формула 6.20):
– показывает степень согласованности мнений экспертов по важности каждого из оцениваемых параметров. Рассчитывается (формула 6.20): (ф. 6.20)
(ф. 6.20) - количество экспертов;
- количество экспертов; - количество параметров;
- количество параметров; - отклонение суммы рангов по j-му параметру от среднего значения суммы рангов.
- отклонение суммы рангов по j-му параметру от среднего значения суммы рангов. (ф. 6.21)
(ф. 6.21) – полная согласованность мнений экспертов, если
– полная согласованность мнений экспертов, если  - полная несогласованность мнений экспертов.
- полная несогласованность мнений экспертов. - числом натурального ряда таким образом, что значение 1 дается максимальной оценке, а n- минимальной; если среди оценок, данных i-ым экспертом, есть одинаковые, то этим оценкам присваивается одинаковый ранг, равный среднему арифметическому соответствующих чисел натурального ряда, например, если максимальное количество баллов получили одновременно два направления, то их ранг можно рассчитать как (1+2):2, и следующий объект получит ранг, равный 3; если же максимальное количество баллов получили одновременно три направления, то каждое из них получит ранг равный (1+2+3):3 =2, а следующий по значимости объект получит ранг, равный 4;
- числом натурального ряда таким образом, что значение 1 дается максимальной оценке, а n- минимальной; если среди оценок, данных i-ым экспертом, есть одинаковые, то этим оценкам присваивается одинаковый ранг, равный среднему арифметическому соответствующих чисел натурального ряда, например, если максимальное количество баллов получили одновременно два направления, то их ранг можно рассчитать как (1+2):2, и следующий объект получит ранг, равный 3; если же максимальное количество баллов получили одновременно три направления, то каждое из них получит ранг равный (1+2+3):3 =2, а следующий по значимости объект получит ранг, равный 4; (формула 6.22):
(формула 6.22): (ф. 6.22)
(ф. 6.22) (формула 6.23):
(формула 6.23): (ф. 6.23)
(ф. 6.23) - номер направления;
- номер направления; ) (формула 6.24):
) (формула 6.24): (ф. 6.24)
(ф. 6.24) (ф. 6.25)
(ф. 6.25) -количество равных рангов в
-количество равных рангов в 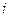 -й группе;
-й группе;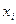 >
>  ;
;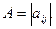 (ф. 6.26)
(ф. 6.26) если
если 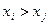 ;
;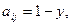 если
если  ;
;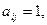 если
если  , где
, где 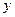 - любое рациональное число в заданном интервале.
- любое рациональное число в заданном интервале.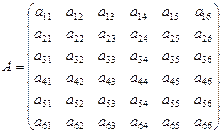
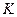 параметров в виде матрицы-столбца
параметров в виде матрицы-столбца 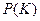 , которая определяется (формула 6.27):
, которая определяется (формула 6.27):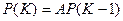 , где
, где 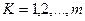 . (ф. 6.27)
. (ф. 6.27)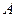 на столбец матрицы
на столбец матрицы 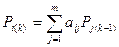 . (ф. 6.28)
. (ф. 6.28) , то есть для определения
, то есть для определения 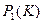 берется
берется 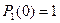 :
: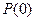 .
.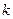 - го порядка
- го порядка  , именно она трактуется как значение коэффициента весомости
, именно она трактуется как значение коэффициента весомости  ; (ф. 6.29)
; (ф. 6.29) . (ф. 6.30)
. (ф. 6.30)