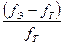|
|
I. Анализ и прогнозирование тенденции.1. Оценка аномальных наблюдений на основе λ- и q-статистик. 2. Расчет аналитических ( Δi, Тр и Тпр) и средних ( 3. Определение наличия тенденции средней и дисперсии в рядах динамики и вычисление уравнения тренда. - Определение тенденции по видам: среднего уровня и дисперсии. - Определение наличия тенденции автокорреляции (для связных рядов динамики). - Выявление основной тенденции динамического ряда. - Оценка адекватности выбранного уравнения тренда. - Корреляция рядов динамики. - Прогнозирование динамики на основе простейших методов. II. Выявление периодической компоненты. Модели сезонных колебаний: - графический анализ исходных данных; - выявление тенденции средней и дисперсии; - проверка ряда динамики на наличие сезонной компоненты на основе критериев «пиков», «ям» и др.; - расчет параметров уравнения тренда и определение теоретических уровней ряда динамики по тренду; - определение абсолютных и относительных отклонений фактических уровней от тренда. Графический метод в анализе амплитуды отклонений эмпирических и теоретических значений уровней ряда динамики; - проверка абсолютных и относительных отклонений фактических уровней от выравненных по тренду на наличие автокорреляции; - построение модели сезонной волны по отклонениям фактических данных от тренда методами гармонического анализа. Определение гармоники Фурье, наилучшим образом отражающей периодичность изменения уровней ряда динамики на основе: - минимизации суммы квадратов отклонений эмпирических данных от выравненных по гармонике; - расчета средней квадратической ошибки. Рассмотрим реализацию данных методик на конкретных примерах. Пример.Проведем комплексный экономико-статистический анализ деловой активности и прибыльности 48 крупнейших банков России на 1.01.97 г. (табл. 13.1). Определим факторы развития банковской системы. Задача реализована с использованием стандартных пакетов прикладных программ «Олимп» и АРМ «Статистика». Таблица 13.1 Основные показатели деятельности банков России на 1.01.97 г. (тыс. руб.)
Продолжение
Анализ исходных данных о деятельности коммерческих банков России начинаем с априорного анализа. Методику априорного анализа покажем на примере одного из показателей – балансовой прибыли, так как этот показатель является результативным. Построим ряд распределения банков по величине балансовой прибыли (табл. 13.2). Таблица 13.2 Распределение банков РФ по величине балансовой прибыли
Данные табл. 13.2 свидетельствуют о высоком удельном весе (75,0%) в рассматриваемой совокупности небольших среди крупнейших банков по величине балансовой прибыли. Недостатком полученного ряда распределения является то, что есть группы, содержащие менее 5 единиц наблюдения, что не может отражать закономерности развития по данным группам банков. Однако, принимая во внимание условность исходных данных, проанализируем ряд распределения коммерческих банков в том виде, как он представлен в табл. 13.2. По результатам табл. 13.2 видно, что банки с балансовой прибылью более 605316 тыс. руб. являются аномальными для рассматриваемой совокупности. В целом дальнейший анализ может быть проведен в двух направлениях: либо по всей первоначально рассмотренной совокупности банков, предполагая аномальность, вызванную объективно существующими причинами, либо отдельно анализ 75,0% банков (так как это составляет более 50% объема выборки) и отдельно анализ оставшихся банков. При решении данной задачи мы будем руководствоваться первым направлением. Графически распределение банков по величине балансовой прибыли можно представить в виде гистограммы и полигона распределения (рис. 13.1).
Рис. 13.1.Гистограмма и полигон распределения банков РФ по величине балансовой прибыли Анализируя график, видно, что распределение островершинное и правостороннее, что подтверждается анализом выборочных характеристик:
В рассматриваемой совокупности крупнейших банков России наиболее часто встречаются банки с величиной балансовой прибыли 113639 тыс. руб.
Величина медианы свидетельствует о том, что 50% банков имеют балансовую прибыль не более 136 316 тыс. руб. Коэффициент асимметрии: AS = 1,86 > 0 – правосторонняя асимметрия. Это же подтверждается и выражением вида: ( Оценка существенности асимметрии подтвердила ранее сформулированные выводы:
Так как AS = 0,7 > 0,5, то асимметрия ряда распределения балансовой прибыли считается существенной. Коэффициент эксцесса ЕX= 3,05 > 0, что свидетельствует об островершинном распределении. В целом анализ выборочных характеристик Me <
где fЭ – эмпирические значения признака; fТ – теоретические значения признака. Расчет теоретических частот осуществляется по формуле вида
где N – объем совокупности; h – ширина интервала, σ – среднее квадратическое отклонение; f(t) – табулированные значения функции хi – середина интервала;
Охарактеризуем закон распределения коммерческих банков РФ по величине балансовой прибыли (табл. 13.3).
Таблица 13.3 Расчетная таблица для определения расчетного значения χ2-критерия
Аналогичный подробный анализ должен быть проведен по всем анализируемым признакам. После подробного анализа характера распределения необходимо перейти к следующему этапу построения модели. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ) показателей рядов динамики и на их основе анализ тенденций и закономерностей развития социально-экономических явлений.
) показателей рядов динамики и на их основе анализ тенденций и закономерностей развития социально-экономических явлений.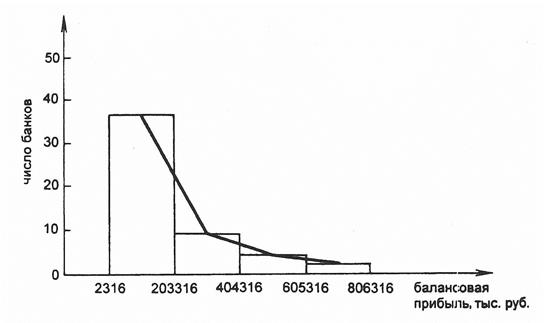
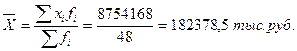
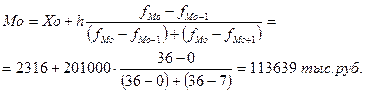
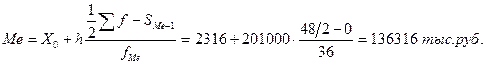
 - Мо) = 182378,5 – 113639 = 68739,5 > 0.
- Мо) = 182378,5 – 113639 = 68739,5 > 0. .
. ,
, ,
, , для нормального закона распределения (приложение 4), где
, для нормального закона распределения (приложение 4), где 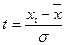 ;
; (α = 0,90, v = k – 3 = 1).
(α = 0,90, v = k – 3 = 1). , следовательно, гипотеза о случайности расхождения между частотами эмпирического и теоретического распределения отвергается.
, следовательно, гипотеза о случайности расхождения между частотами эмпирического и теоретического распределения отвергается.