
|
|
Методические указания и решение типовых задач
Данная глава знакомит студентов с задачами, решение которых дает возможность усвоить правила построения и анализа рядов динамики для характеристики изменения социально-экономических явлений во времени, выявления основной тенденции, закономерностей их развития. Достигается это соответствующей обработкой рядов динамики, анализом изменения его уровней, расчетом аналитических показателей. Это важный раздел курса теории статистики, так как в большинстве случаев задачей статистического исследования бывает анализ развития тех или иных явлений. Виды рядов динамики. Показатели динамики.Начиная изучение темы, необходимо обратить внимание на классификацию рядов динамики, различия между ними, так как отнесение ряда динамики к тому или иному виду имеет важное значение для их изучения. Выбор соответствующих приемов и способов анализа определяется характером исходных данных и зависит от задач исследования. В зависимости от способа выражения уровней(в виде абсолютных, относительных и средних величин) ряды динамики подразделяются на ряды абсолютных, относительных и средних величин. В зависимости от того, выражают уровни ряда состояние явления на определенные моменты времени(на начало месяца, квартала, года и т.п.) или его величину за определенные интервалы времени(например, за сутки, месяц, год и т.п.), различают соответственно моментные и интервальные ряды. Ряды динамики могут быть с равноотстоящими (по времени) уровнями и неравноотстоящими (по времени) уровнями. Например, имеются данные о выпуске книг и брошюр, журналов и газет в Российской Федерации (тыс. печатных единиц):
Годы 1990 1991 1992 1993 1994 41,2 34,0 28,7 29,0 30,4 Это интервальный ряд динамики абсолютных величин с равноотстоящими уровнями во времени. Его уровни характеризуют суммарный итог выпуска книг и брошюр за четко определенный отрезок времени (за каждый год). Уровни интервального ряда динамики могут быть суммированы, так как не содержат повторного счета. Примером моментного ряда абсолютных величин с равноотстоящими уровнями во времени может служить ряд динамики, показывающий число постоянных дошкольных учреждений в России (на конец года), тыс.: Годы 1990 1991 1992 1993 1994 1995 87,9 87,6 82,0 78,3 72,8 68,6 Уровни этого ряда – обобщенные итоги учета числа дошкольных учреждений по состоянию на определенную дату (конец каждого года). Отдельные уровни моментного ряда динамики содержат элементы повторного счета, так как отдельные дошкольные учреждения, учитываемые, например, в 1990 г., существуют и в настоящее время, являясь единицами совокупности и в 1995 г. Все это делает бессмысленным суммирование уровней моментных рядов динамики. Примером интервального ряда динамики средних величин с неравноотстоящими уровнями во времени может служить ряд динамики среднемесячной заработной платы и выплат социального характера в России в 1995 г., в долл. США:
Его уровни относятся к помесячным интервалам времени, но суммирование их самостоятельного значения не имеет Примером моментного ряда динамики относительных величин с равноотстоящими уровнями во времени может служить ряд динамики, характеризующий удельный вес численности городского и сельского населения в общей численности населения (на начало года), %:
Суммирование уровней данного ряда не имеет смысла. Одним из важнейших направлений анализа рядов динамики является изучение особенностей развития явления за отдельные периоды времени. Для выявления специфики развития изучаемых явлений за отдельные периоды времени определяют абсолютные и относительные показатели изменения ряда динамики: абсолютные приросты, абсолютное значение одного процента прироста, темпа роста и прироста. Выяснение сущности этих показателей, их взаимосвязей, методов расчета – необходимое условие усвоения данной темы. Рассматривая данные показатели, необходимо правильно выбирать базу сравнения, которая зависит от цели исследования. При сравнении каждого уровня ряда с предыдущим получаются цепные показатели; при сравнении каждого уровня с одним и тем же уровнем (базой) получают базовые показатели. Например, требуется провести анализ динамики продажи мясных консервов за 1993-1997 гг. Для удобства и наглядности исходные и рассчитанные показатели изложены в табличной форме (табл. 10.1).
Таблица 10.1 Динамика продажи мясных консервов в одном из регионов за 1993-1997 гг. и расчет аналитических показателей динамики (данные условные)
Для выражения абсолютной скорости роста (снижения) уровня ряда динамики исчисляют статистический показатель – абсолютный прирост (Д). Его величина определяется как разность двух сравниваемых уровней. Она вычисляется по формуле Δц = уi – yi-1 или Δб = уi – y0 где уi – уровень i-го года; у0 – уровень базисного года. Например, абсолютное уменьшение продажи консервов за 1994 г. по сравнению с 1993 г. составило: 806 – 891 = -85 млн. усл. банок (табл. 10.1, гр. 2), а по сравнению с базисным 1993 г. продажа консервов в 1997 г. возросла на 760 млн. усл. банок (гр. 3). Интенсивность изменения уровней ряда динамики оценивается отношением текущего уровня к предыдущему или базисному, которое всегда представляет собой положительное число. Этот показатель принято называть темпом роста (Тр). Он выражается в процентах, т.е.
Так, для 1997 г. темп роста по сравнению с 1993 г. составил Темп роста может быть выражен и в виде коэффициента (Кр). В этом случае он показывает, во сколько раз данный уровень ряда больше уровня базисного года или какую его часть он составляет. Для выражения изменения величины абсолютного прироста уровней ряда динамики в относительных величинах определяется темп прироста (Тпр), который рассчитывается как отношение абсолютного прироста к предыдущему или базисному уровню, т.е.
Темп прироста может быть вычислен также путем вычитания из темпов роста 100%, т.е. Тпр = Т – 100. В нашем примере (табл. 10.1, гр. 6, 7) он показывает, например, на сколько процентов продажа консервов в 1997 г. возросла по сравнению с 1993 г.: Показатель абсолютного значения одного процента прироста(|%|) определяется как результат деления абсолютного прироста на соответствующий темп прироста, выраженный в процентах, т.е. Для 1997 г. абсолютное значение 1% прироста (табл. 10.1, гр. 8) равно: 0,01 · 16,37 = 16,37, или Особое внимание следует уделять методам расчета средних показателейрядов динамики, которые являются обобщающей характеристикой его абсолютных уровней, абсолютной скорости и интенсивности изменения уровней ряда динамики. Различают следующие средние показатели: средний уровень ряда динамики, средний абсолютный прирост, средний темп роста и прироста. Методы расчета среднего уровняряда динамики зависят от его вида и способов получения статистических данных. В интервальном ряду динамики с равноотстоящимиуровнями во времени расчет среднего уровня ряда (
В нашем примере средняя продажа мясных консервов за 5 лет составила: Если интервальный ряд динамики имеет неравноотстоящиеуровни, то средний уровень ряда вычисляется по формуле
где t – число периодов времени, в течение которых уровень не изменяется. Для моментного ряда с равноотстоящимиуровнями средняя хронологическаярассчитывается по формуле
где n – число уровней ряда. Средняя хронологическая для неравноотстоящих уровней моментного ряда динамики вычисляется по формуле
Определение среднего абсолютного приростапроизводится по цепным абсолютным приростам по формуле: Среднегодовой темп роставычисляется по формуле средней геометрической:
где m – число коэффициентов роста Среднегодовой темп ростапродажи мясных консервов за 1993-1997 гг. рассчитаем двумя способами:
Среднегодовой темп приростаполучим, вычтя из среднего темпа роста 100%. В нашем примере
Приемы обработки и анализа рядов динамики.При анализе рядов динамики иногда возникает необходимость смыкания рядов, т.е. объединение двух и более рядов, характеризующих изменение явления, в один ряд. Смыкание необходимо в случаях, когда уровни ряда несопоставимы в связи с территориальными или ведомственными, организационными изменениями, изменением методологии исчисления и т.п. Существует несколько способов приведения рядов динамики к сопоставимому виду. Например, имеются данные, характеризующие общий объем продукции промышленности в одном из регионов (в фактически действовавших ценах), млн. руб.:
Для приведения ряда динамики к сопоставимому виду для 1994 г. определим коэффициент соотношения уровней двух рядов:
Умножая на этот коэффициент уровни первого ряда, получаем их сопоставимость с уровнями второго ряда, млн руб.: 1991 г. – 20,1 · 1,12 = 22,5; 1992 г. – 20,7 · 1,12 = 23,2; 1993 г. – 21,0 · 1,12 = 23,5. Получен сопоставимый ряд динамики общего объема продукции промышленности (в фактически действовавших ценах, в структуре и методологии соответствующих лет) в одном из регионов (в новых границах, млн. руб.):
Другой способ смыкания рядов динамики заключается в том, что уровни года, в котором произошли изменения (в нашем примере уровни 1994 г.), как до изменений, так и после изменений (для нашего примера в старых и новых границах, т.е. 21,2 и 23,8) принимаются за 100%, а остальные – пересчитываются в процентах по отношению к этим уровням соответственно (в нашем примере до изменений – по отношению к 21,2, а после изменений - по отношению к 23,8). В результате получается сомкнутый ряд. Применив этот способ для нашего примера, получим следующий ряд динамики, характеризующий общий объем продукции региона:
Выявление основной тенденции ряда динамики.Важной задачей статистики при анализе рядов динамики является определение основной тенденции развития. При изучении в рядах динамики основной тенденции развития явления применяются различные приемы и методы. Одним из приемов выявления основной тенденции является метод укрупнения интервалов.Этот способ основан на укрупнении периодов времени, к которым относятся уровни ряда. Например, ряд ежесуточного выпуска продукции заменяется рядом месячного выпуска продукции и т.д. Другой прием – метод скользящей средней.Суть метода состоит в замене абсолютных данных средними арифметическими за определенные периоды. Расчет средних ведется способом скольжения, т.е. постепенным исключением из принятого периода скольжения первого уровня и включением следующего. Например, на основе данных о производстве стиральных машин фирмой за 15 месяцев 1996-1997 гг. нужно произвести сглаживание ряда методом трехчленной и четырехчленной скользящей средней (табл. 10.2). Таблица 10.2 Динамика производства стиральных машин и расчет скользящих средних
Взяв данные за первые три месяца, исчисляем трехчленные суммы, а затем среднюю:
Интервал скольжения можно также брать четный (четыре, шесть и т.д.). Нахождение скользящей средней по четному числу членов осложняется тем, что средняя может быть отнесена только к середине между двумя датами. Чтобы ликвидировать этот сдвиг, применяется центрирование, т.е. нахождение средней из средних для отнесения полученного уровня к определенной дате. При центрировании необходимо также находить скользящие суммы, скользящие средние по этим суммам и средние из средних. Пример сглаживания ряда методом четырехчленной скользящей средней представлен в табл. 10.2 (графы 4, 5, 6). Наиболее эффективным способом выявления основной тенденции развития является аналитическое выравнивание.При этом уровни ряда динамики выражаются в виде функции времени: Аналитическое выравнивание может быть осуществлено по любому рациональному многочлену. Выбор функции производится на основе анализа характера закономерностей динамики данного явления. Рассмотрим применение метода аналитического выравнивания по прямой для выражения основной тенденции на следующем примере. В табл. 10.3 приведены исходные и расчетные данные о динамике производства молока в регионе за 1993-1997 гг.
Таблица 10.3 Исходные и расчетные данные для определения параметров системы уравнения (млн. т.)
Для выравнивания ряда динамики по прямой используем уравнение Способ наименьших квадратов дает систему двух нормальных уравнений для нахождения параметров а0 и а1:
где у – исходный уровень ряда динамики; n – число членов ряда; t – показатель времени, который обозначается порядковыми номерами, начиная от низшего. Например: Годы 1993 1994 1995 1996 1997 t 1 2 3 4 5 Решение системы уравнений позволяет получить выражения для параметров а0 и a1:
В рядах динамики техника расчета параметров уравнения может быть упрощена. Для этой цели показателем времени t придают такие значения, чтобы их сумма была равна нулю, т.е.Σt = 0. В нашем примере число исходных уровней ряда нечетное (n = 5) (табл. 10.3). При этом уравнения системы примут следующий вид: na0 = Σy и a1Σt2 = Σty, откуда:
Расчет необходимых значений дан в табл. 10.3. По итоговым данным определяем параметры уравнения:
В результате получаем следующее уравнение основной тенденции производства молока в регионе за 1993-1997 гг.:
Подставляя в уравнение принятые обозначения t, вычислим выровненные уровни ряда динамики: 1993 г. – 1994 г. – и т.д. (см. значения По окончании расчета основной тенденции целесообразно построить график, на котором следует изобразить исходные данные и теоретические значения уровней ряда. Однако если число уровней ряда четное, то условное обозначение показателя времени принимает следующий вид: Годы 1992 1993 1994 1995 1996 1997 t -5 -3 -1 +1 +3 +5 (это означает, что счет времени ведется полугодиями). Основная тенденция (тренд) показывает, как воздействуют систематические факторы на уровень ряда динамики, а колеблемость уровней около тренда служит мерой воздействия остаточных факторов. Ее можно измерить по формуле
Используя данные этого примера, рассчитаем показатель колеблемости производства молока в регионе (табл. 10.3):
Относительной мерой колеблемости является коэффициент вариации:который вычисляется по формуле
В нашем примере При анализе рядов динамики важное значение имеет выявление сезонных колебаний.Этим колебаниям свойственны более или менее устойчивые изменения уровней ряда по внутригодовым периодам: месяцам, кварталам, Для выявления сезонных колебаний обычно анализируются месячные и квартальные уровни ряда динамики за год или за несколько лет. При изучении сезонных колебаний используются специальные показатели – индексы сезонности (IS). Способы определения индексов сезонности различны; они зависят от характера основной сезонности ряда динамики. Для ряда внутригодовой динамики, в которой основная тенденция роста незначительна (или она не наблюдается совсем), изучение сезонности основано на методе постоянной средней:являющейся средней из всех рассматриваемых уровней. Самый простой способ заключается в следующем: для каждого года рассчитывается средний уровень, а затем с ним сопоставляется (в процентах) уровень каждого месяца. Это процентное отношение обычно именуется индексом сезонности:
Рассмотрим табл. 10.4. Таблица 10.4 Численность рабочих фирмы по месяцам
В приведенном примере средний уровень ряда составляет:
Индекс сезонности составляет для января
где у – общий средний месячный уровень за 3 года. Проиллюстрируем этот расчет на условном примере (табл. 10.5). Для получения значений Таблица 10.5 Внутригодовая динамика числа расторгнутых браков населением города по месяцам за 1995-1997 гг.
январь февраль . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . декабрь Определим осредненные значения уровней ряда у, для каждого месяца годового цикла (табл. 10.5): январь февраль Далее по исчисленным месячным средним уровням
где n – число месяцев. Значение общего среднего уровня можно вычислить также и по итоговым данным за отдельные годы:
где m – число лет;
И наконец, определим по месяцам года индексы сезонности: январь февраль Совокупность исчисленных для каждого месяца годового цикла индексов сезонности характеризует сезонную волну развития числа расторгнутых браков в городе во внутригодовой динамике. Для получения наглядного представления о сезонной волне желательно изобразить полученные данные в виде линейной диаграммы. При наличии ярко выраженной тенденции к увеличению или уменьшению уровней из года в год применимы другие способы измерения сезонных колебаний, в частности индексы сезонности определяются на основе методов,которые позволяют исключить влияние тенденции роста (падения). При использовании способа аналитического выравнивания ход вычислений следующий: 1) вычисляют для каждого месяца (квартала) выравненные уровни по соответствующему аналитическому уравнению на момент времени t; 2) берут отношение фактических месячных (квартальных) данных (уi) к соответствующим им выравненным данным в процентах:
3) находят среднюю из этих отношений для одноименных месяцев (кварталов) в процентах:
где n – число одноименных месяцев 4) из полученных 12 помесячных относительных величин ( 5) определяют индексы сезонности по формуле
где уi – исходные уровни ряда,
n – число годовых периодов Та же методика расчета индексов сезонности применяется и при использовании метода скользящей средней. В качестве аналитической формы сезонной волны иногда применяется уравнение следующего вида:
где k – степень точности гармоники тригонометрического многочлена; t - время. Это уравнение представляет собой ряд Фурье, где время (t) выражается в радиальной мере или в градусах:
Обычно при выравнивании по ряду Фурье рассчитывают не более четырех гармоник и затем уже определяют, с каким числом гармоник наилучшим образом отражается периодичность изменения уровней ряда. Например, при k = 1 уравнение Фурье будет иметь вид:
При k = 2 соответственно
Параметры уравнения выравненных уровней, определяемых рядом Фурье, находят по способу наименьших квадратов. Не излагая здесь вывода, приведем готовые формулы, используемые для исчисления указанных выше параметров уравнения ряда Фурье:
Покажем выравнивание по ряду Фурье на условных данных о продаже молока на рынках сельхозпродуктов города (табл. 10.6). Таблица 10.6 Динамика продажи молока на рынках сельхозпродуктов города и расчет параметров системы уравнения по ряду Фурье
В этой же таблице содержатся произведения у·cost, у·sint, необходимые для определения параметров уравнения по первой гармонике. На основе полученных итоговых данных табл. 10.6 находим:
Отсюда: Подставляя в это уравнение значения cost и sint (из таблицы приложения 11), получаем теоретические значения количества проданного молока Параметры гармоники второго
и высшего порядка рассчитываются аналогично, и их значения последовательно присоединяются к значениям первой гармоники. Опустив расчеты, запишем уравнение для выравнивания нашего ряда с учетом второй гармоники:
Подставив в уравнение конкретные значения cost, sint, sin2t, cos2t, получим выравненные уровни проданного молока по месяцам. Затем, рассчитав остаточные дисперсии При изучении рядов динамики возникает необходимость получения сравнительных характеристик направления и интенсивности роста одновременно развивающихся во времени явлений. Это достигается путем приведения рядов динамики к общему (единому) основанию. По исходным уровням нескольких рядов динамики определяются относительные величины - базисные темпы роста и прироста. Принятый при этом за базу сравнения период (момент) времени выступает в качестве постоянной базы расчета темпов роста для каждого из изучаемых рядов динамики. Рассмотрим примерприведения рядов динамики к общему основанию на данных о производстве цемента в двух странах, млн. т.:
Различные значения абсолютных уровней приведенных рядов динамики затрудняют выявление особенностей производства цемента в стране А и стране Б. Приведем абсолютные уровни рядов динамики к общему основанию, приняв за постоянную базу сравнения 1993 г., и получим данные, в процентах к 1993 г.:
Из этих данных видно, что производство цемента в стране А непрерывно и быстро возрастает, значительно превосходя темпы роста в стране Б. Если в 1997 г. производство цемента в стране А возросло по сравнению с 1993 г. в 2,8 раза, то в стране Б оно увеличилось за это же время в 1,19 раза. Сопоставив базисные темпы роста производства цемента в стране А и стране Б, получим коэффициент опережения – относительный показатель, характеризующий опережение (больше единицы) или отставание (меньше единицы) в развитии стран: При изучении развития явления во времени часто возникает необходимость оценить степень взаимосвязи в изменениях уровней двух рядов динамики различного содержания, но связанных между собой. Эта задача решается методами коррелирования:а) уровней рядов динамики; б) отклонений фактических от выравненных уровней; б) абсолютных разностей. Первый способ правильно показывает тесноту связи между явлениями лишь в том случае, если в каждом из них отсутствует автокорреляция, т.е. зависимость между последовательными уровнями ряда динамики. На условном примере данных об изменении объема собственной продукции фирмы общественного питания и доходов от реализации товаров общественного питания за 1988-1997 гг. рассмотрим применение коррелирования уровней для измерения связи между рядами динамики (табл. 10.7). Таблица 10.7 Исходные и расчетные данные для определения коэффициента корреляции

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. (табл. 10.1, гр. 5).
(табл. 10.1, гр. 5).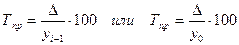
 , или 185,3 – 100 = 85,3%.
, или 185,3 – 100 = 85,3%.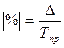 или 0,01 · уi-1. Расчет этого показателя имеет экономический смысл только на цепной основе.
или 0,01 · уi-1. Расчет этого показателя имеет экономический смысл только на цепной основе. млн. усл. банок.
млн. усл. банок. ) производится по формуле средней арифметической простой:
) производится по формуле средней арифметической простой: .
.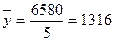 млн. усл. банок.
млн. усл. банок. ,
,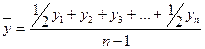 ,
,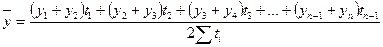 .
. или
или 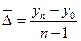 . Среднегодовой абсолютный прирост продажи мясных консервов за 1993-1997 гг. равен:
. Среднегодовой абсолютный прирост продажи мясных консервов за 1993-1997 гг. равен: 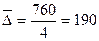 или
или  млн. усл. банок.
млн. усл. банок. ,
, ;
;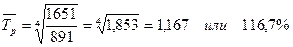 .
. .
. .
.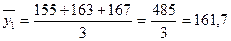 ;
;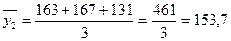 и т.д.
и т.д. .
.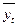


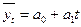 .
.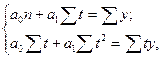
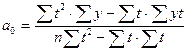 ;
;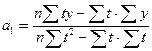 .
.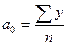 представляет собой средний уровень ряда динамики (
представляет собой средний уровень ряда динамики (  .
.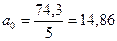 ;
;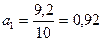 .
.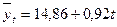 .
. = 14,86 + 0,92 (-2) = 13,02;
= 14,86 + 0,92 (-2) = 13,02;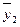 = 14,86 + 0,92 (-1) = 13,94
= 14,86 + 0,92 (-1) = 13,94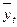 в табл. 10.3).
в табл. 10.3).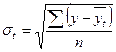 – среднее квадратическое отклонение.
– среднее квадратическое отклонение.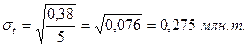
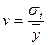 .
.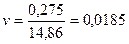 или 1,85%.
или 1,85%.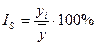 .
.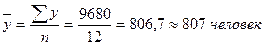 .
. ; для февраля
; для февраля 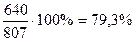 и т.д. Однако помесячные данные одного года в силу элемента случайности слишком ненадежные для выявления закономерности колебаний. Поэтому на практике для выявления закономерности колебаний пользуются помесячными данными за ряд лет (в основном не менее 3 лет). Тогда для каждого месяца рассчитывается средняя величина уровня за три года, затем рассчитывается среднемесячный уровень для всего ряда и в заключение определяется процентное отношение средних для каждого месяца к общему среднемесячному уровню ряда, т.е.
и т.д. Однако помесячные данные одного года в силу элемента случайности слишком ненадежные для выявления закономерности колебаний. Поэтому на практике для выявления закономерности колебаний пользуются помесячными данными за ряд лет (в основном не менее 3 лет). Тогда для каждого месяца рассчитывается средняя величина уровня за три года, затем рассчитывается среднемесячный уровень для всего ряда и в заключение определяется процентное отношение средних для каждого месяца к общему среднемесячному уровню ряда, т.е.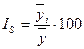 ,
, – средняя для каждого месяца за 3 года;
– средняя для каждого месяца за 3 года; по способу средней простой (невзвешенной) произведем осреднение уровней одноименных периодов:
по способу средней простой (невзвешенной) произведем осреднение уровней одноименных периодов: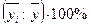
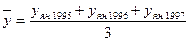 ;
;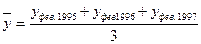 ;
;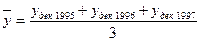 .
. ;
;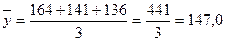 и т.д.
и т.д.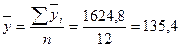
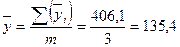
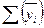 – сумма среднегодовых уровней ряда динамики.
– сумма среднегодовых уровней ряда динамики. ;
;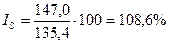 и т.д.
и т.д.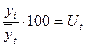 ;
; ;
;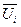 ) вычисляют общий среднемесячный уровень (
) вычисляют общий среднемесячный уровень ( 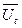 );
);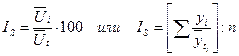 ,
,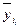 – выравненные (теоретические) уровни ряда,
– выравненные (теоретические) уровни ряда,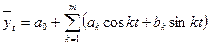
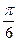
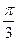
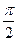
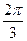
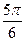

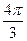
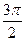
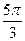

 .
. .
. .
.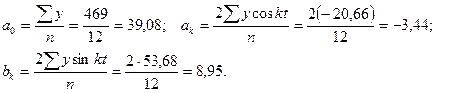
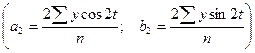
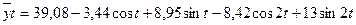 .
.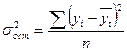 для двух случаев, можно сделать вывод, какая гармоника ряда Фурье наиболее близка к фактическим уровням ряда.
для двух случаев, можно сделать вывод, какая гармоника ряда Фурье наиболее близка к фактическим уровням ряда.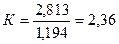 раза, т.е. производство цемента в стране А развивалось за 1993-1997 гг. в 2,36 раза быстрее, чем в стране Б.
раза, т.е. производство цемента в стране А развивалось за 1993-1997 гг. в 2,36 раза быстрее, чем в стране Б.