
|
|
Процессы растворения твердых веществ в природных водах
Для описания процессов взаимодействия между твердыми веществами и природными водами в настоящее время широко используются методы равновесной термодинамики. В общем виде такое взаимодействие можно представить уравнением
Константа равновесия этого процесса может быть определена из уравнения
где Креакц – константа равновесия процесса растворения; ai– активность продуктов и реагентов при установлении равновесия в степени, соответствующей их стехиометрическому коэффициенту. Численное значение константы равновесия в стандартных условиях (температура 298К, давление 101,3 кПа) может быть определено через величину энергии Гиббса реакции, которая, в свою очередь, может быть легко рассчитана по разности между суммой энергий Гиббса образования из простых веществ продуктов реакции и суммой энергий Гиббса образования реагентов, для стандартных условий:
где R– универсальная газовая постоянная, Дж/(моль . К); Т0 – температура при стандартных условиях, 298 К); 2,3 – коэффициент перехода от значения в натуральных логарифмах к значению в десятичных логарифмах. Значения энергии Гиббса образования ионов и молекул широко представлены в справочной литературе, некоторые из них приводятся в таблице 1 Приложения. Основными факторами, оказывающими влияние на значение константы равновесия процесса растворения, являются температура и давление. Значение константы равновесия при температуре, отличающейся от стандартных условий, может быть определено по уравнению
где К0, Т0 и К1, Т1– константы равновесия и температуры реакций в стандартных и рассматриваемых условиях соответственно; DНреакц – значение энтальпии реакции, равное разности между суммой энтальпий продуктов и суммой энтальпий реагентов; R – универсальная газовая постоянная. Для большинства реакций растворения, протекающих в природных условиях, DНреакц меняется в пределах от –20 до +20 кДж/моль. При таких изменениях энтальпии реакции для температуры 338 К, которая представляется максимальной для большинства поверхностных вод, логарифм отношения констант равновесия будет изменяться примерно от –4 до +4: –4 Таким образом, для большинства реакций растворения, протекающих в поверхностных водах, максимальное изменение константы равновесия может составлять от 0,4 до 2,5 от соответствующего значения К0: 0,4К0 Такие изменения константы равновесия представляются значительными, поэтому при оценке растворимости твердых веществ в природных условиях необходимо учитывать влияние температуры на процесс растворения. Влияние давления на значение константы равновесия можно оценить по уравнению:
где К1и К0– константы равновесия при общем давлении Р и 1 атм соответственно; DV – изменение молярного объема в процессереакции, см3/моль; R – универсальная газовая постоянная, см3 . атм/(град . моль); Т0 – значение температуры при стандартных условиях, 298 К. Для большинства процессов растворения твердых соединений в природных условиях изменение молярного объема не превышает 40 см3/моль. Поэтому при увеличении давления до 100 атм логарифм отношения констант равновесия будет равен примерно: lg(K1/K0) » 0,07. (7) В этом случае значение константы равновесия будет отличаться от значения константы равновесия при стандартных условиях примерно на 17%. Следовательно, влияние давления на процесс растворения твердых веществ в природных водах целесообразно учитывать для подземных вод и глубинных вод океанов и морей лишь тогда, когда давление в системе вода – порода значительно превышает атмосферное. Важными характеристиками природных вод и твердых веществ при рассмотрении процессов растворения являются часто используемые в зарубежной литературе показатели агрессивности и неустойчивости. Показатель агрессивностиприродных вод характеризует способность данной воды перевести твердое вещество в раствор. Численное значение показателя агрессивности по отношению к данному веществу определяется величиной логарифма отношения константы равновесия к частному от деления произведения активности ионов (продуктов), образующихся в процессе растворения и содержащихся в данной воде, на произведение активности реагентов, содержащихся в растворяемом веществе:
где А – показатель агрессивности воды; К – константа равновесия процесса растворения данного вещества; ПА – произведение активностей продуктов реакции, содержащихся в данной воде, и реагентов, содержащихся в растворяемом веществе, соответственно. Показатель агрессивности воды часто используют для сравнения растворяющей способности природных вод. Чем больше 4, тем в большей степени система неравновесна и тем более интенсивно протекает процесс растворения данного вещества. Показатель неустойчивостихарактеризует степень удаленности системы от состояния равновесия. Этот показатель удобно использовать при сравнении устойчивости различных твердых веществ по отношению к одной и той же природной воде. Чем больше значение показателя неустойчивости, тем данное вещество менее устойчиво. Показатель неустойчивости I по численному значению равен показателю агрессивности, взятому с обратным знаком: I = –A. (9) Эта величина может быть рассчитана по уравнению
В случае, который достаточно часто встречается в природных условиях, когда растворяется чистое твердое вещество, активность которого может быть принята равной единице, а в водном растворе содержатся только ионы и молекулы Н2О, описание процесса упрощается. Уравнение процесса растворения в этом случае можно представить уравнением АaBb = aA+b + bB–a. (11) Константа равновесия в этом случае равна произведению активностей образующихся ионов в степенях, соответствующих их стехиометрическим коэффициентам:
Для определения направления процессов растворения или осаждения в этом случае удобно использовать показатель степени неравновесности:
где (ПА)прод – произведение активностей ионов в растворе; Кравн – константа равновесия процесса растворения. Степень неравновесности характеризует ненасыщенность ( Константы равновесия процессов растворения, как уже отмечалось выше (уравнение 4), являются величинами, определяемыми термодинамическими параметрами системы. Они связаны соответствующими зависимостями с активностью продуктов процесса растворения (уравнения 3 и 12), поэтому могут быть использованы для определения концентрации соответствующих примесей лишь в any чае бесконечно разбавленных растворов, когда коэффициенты активности всех компонентов равны единице. Для оценки концентрации примесей в растворе часто используют понятие произведения растворимости (ПР), которое для процесса, представленного уравнением (11), будет иметь вид: ПР = [А+b]а[В–а]b, (14) где [А+Ь]а и [В-а]b – концентрации ионов в растворе (моль/л) в степени, соответствующей стехиометрическому коэффициенту реакции (11). Произведение растворимости и константа равновесия процесса растворения связаны между собой. Так, для реакции (11) эту связь можно представить уравнением ПР = Kравн/(g где g Значения коэффициентов активности ионов можно рассчитать по уравнениям Дебая – Хюккеля
или по уравнению
где Аи В– константы, зависящие от температуры и давления; а– константа, характеризующая радиус гидратированного иона (зависит от природы иона); I – ионная сила раствора, которая равна
где Сi– концентрации ионов, присутствующих в растворе; zi – заряды соответствующих ионов. Значения коэффициентов А. В и а приводятся в справочнойлитературе, некоторые из них представлены в таблица 8 Приложения.
Жесткость природных вод
Одной из важных характеристик природных вод, во многом определяющих возможности их использования человеком, является жесткость воды. Жесткостью водыназывается свойство воды, обусловленное содержанием в ней ионов кальция и магния. Единицей жесткости воды в нашей стране является моль (жесткости) на кубический метр – моль/м3 (обычно дополнение «жесткости» после слова «моль» опускается). Числовое значение жесткости, выраженное в моль/м3, равно числовому значению жесткости, выраженному в миллиграмм-эквивалентах на литр (мг-экв./л); 1 мг-экв./л соответствует содержанию в воде 20,04 мг/л ионов Са2+ или 12,16мг/л ионов Mg2+. Величину жесткости можно определить по уравнению: Ж = [Са2+]/(МСа2+fСа2+) + [Mg2+]/(MMg2+fMg2+); Ж = где Ж — жесткость воды, моль/л; [Са2+] и [Mg2+] – концентрации ионов кальция и магния, мг/л; fса2+ и fMg2+ – факторы эквивалентности ионов кальция и магния (fса2+ = fмg2+ = 1/2); МСa2+и MMg2+ – молярные массы ионов кальция и магния (МСa2+ = 40,08 г/моль и MMg2+ = 24,32г/моль). Определяемую по уравнению (19) жесткость принято называть общей жесткостьюводы, поскольку в воде различают карбонатную, некарбонатную, устраняемую и неустраняемую жесткость воды. Таблица 4. Классификация природных вод по величине жесткости
Под карбонатной жесткостью понимается количество ионов кальция и магния, связанных с карбонат- и гидрокарбонат-ионами. Поэтому численное значение карбонатной жесткости равно сумме концентраций карбонат- и гидрокарбонат-ионов, выраженных в мг-экв./л. Если эта величина оказывается больше значения общей жесткости т.е. карбонат- и гидрокарбонат-ионы связаны с другими катионами значение карбонатной жесткости принимается равным значению общей жесткости воды. Heкарбонатная жесткость воды определяется как разность значений солей и карбонатной жесткости. Устраненная жесткостьводы представляет собой часть карбонатной жесткости, которая удаляется при кипячении воды. Устраняемую жесткость определяют экспериментально. Неустраняемая жесткостьволы определяется как разность значений сохой и устраняемой жесткости. По величине общей жесткости природные воды принято делить на ряд групп (таблица 4). Среди природных вод наиболее мягкими являются дождевые воды, жесткостькоторых составляет примерно 70-100 ммоль/м3. Жесткость подземных вод меняется в широких пределах – от 0,7 моль/м (грунтовые воды Карелии)до 18-20 моль/м3 (грунтовые воды Донбасса) – и зависит от состава контактирующих с ними горных пород. В речных водах жесткость помимо состава горных пород, контактирующих с питающими данную реку водами, зависит от климатических факторов и испытывает сезонные колебания. Наименьшее значение жесткости речной воды наблюдается в период паводка. За рубежом для выражения значений жесткости воды используются различные единицы измерения. Так, например, немецкий градус жесткости соответствует содержанию в воде 10 мг СаО/л. Один французский градус жесткости соответствует содержанию в воде 10 мг СаСОз/л. Один американский градус жесткости соответствует содержанию в воде 1 мг СаСОз/л. Между этими единицами измерения жесткости можно записать соотношения: 1 моль/м3 = 2,804 немецких градусов жесткости; 1 моль/м3 = 5,005 французских градусов жесткости; 1 моль/м3 = 50,050 американских градусов жесткости.
Примеры решения задач
Пример 6. На сколько миллиграммов в каждом литре воды уменьшится равновесное содержание кислорода в верхнем слое воды природного водоема при увеличении температуры приземного воздуха с 5 до 25°С, если его парциальное давление не изменилось, концентрация кислорода соответствует средним для приземного слоя значениям, давление воздуха соответствует стандартным значениям? Парциальным давлением паров воды можно пренебречь. Решение. Равновесное содержание растворенного кислорода в верхнем слое природного водоема СО2(р-р), в соответствии с законом Генри (уравнение 1), зависит от парциального давления кислорода Ро2 и значения константы Генри, изменяющейся в зависимости от температуры: СО2(р-р) = Кг(О2)РО2. Поскольку по условию задачи парциальное давление кислорода не изменялось, различие равновесных значений концентраций кислорода при температуре 5 и 25°С связано лишь с изменением константы Генри. Поэтому можно записать:
где
Значения константы Генри при различных температурах приводятся в справочной литературе. Некоторые значения представлены в таблицах 3,4 Приложения:
Парциальное давление кислорода можно определить, зная общее давление воздуха Робщ и объемную долю кислорода в приземном слое воздуха
Равновесное содержание кислорода в растворе равно:
Для перевода концентрации в мг/л необходимо умножить полученное значение на величину молярной массы кислорода (32 × 103 мг/моль):
Ответ: содержание кислорода в каждом литре воды уменьшится на 4,1 мг.
Пример 7. Какая природная вода (из двух) более агрессивна по отношению к гипсу (CaSO4 × 2H2O), если активность катионов кальция и анионов SO
Активность гипса в твердой фазе принять равной единице. Температура и давление соответствуют стандартным значениям. Решение: Агрессивность природных вод по отношению к одному и тому же веществу тем выше, чем больше численное значение показателя агрессивности, который, в соответствии с выражением (7), может быть определен по уравнению:
Процесс растворения гипса протекает по уравнению:
По условию задачи необходимо сравнить агрессивность двух различных по составу вод по отношению к одному и тому же соединению, активность которого равна единице, (ПА)реаг = 1. Поэтому можно упростить выражение для показателя агрессивности:
Поскольку значение константы равновесия процесса растворения гипса при заданных условиях – величина постоянная, показатель агрессивности будет тем больше, чем меньше произведения активностей реагентов в воде. Поэтому для решения задачи необходимо сравнить произведения активностей в различных природных водах: для первой воды (ПА)2= для второй воды (ПА)2= Поскольку (ПА)2 < (ПА)1, т.е. (10–4,8 < 10–4,5), вторая природная вода более агрессивна по отношению к гипсу. Ответ: вторая вода более агрессивна по отношению к гипсу.
Пример 8. Какой процесс – растворение или осаждение гипса – будет происходить при его контакте с природной водой, в которой активности катионов кальция и анионов SO Решение. Процесс растворения гипса, как было сказано, можно описать уравнением реакции:
Направление процесса (осаждение или растворение) можно определить по значению показателя степени неравновесности (уравнение 13): Q = (ПА)прод/Кравн. Произведение активностей продуктов процесса растворения гипса в данном случае следует принять равным произведению активностей соответствующих ионов в природной воде, поскольку для этой воды и необходимо определить степень неравновесности. Произведение активностей составит: (ПА)прод = aCa2+a SO Значения константы равновесия реакции растворения гипса можно определить из термодинамических данных по уравнению (4):
Значение
= 28,65 (кДж/моль) = 28,65 . 103 (Дж/моль). Логарифм константы равновесия равен:
Константа равновесия процесса растворения гипса равна:
Значение показателя неравновесности составит: Q = 10–6/(9,4 . 10–6) = 0,1. Поскольку Q< 1, раствор ненасыщен относительно гипса, и идет процесс ого растворения. Ответ: будет происходить растворение гипса. Пример 9. Какой из минералов, не содержащих примесей, – гипс (CaSO4 . 2H2O) или ангидрит (CaSO4) – более устойчив в водном растворе: а) при стандартных условиях; б) при нормальном атмосферном давлении и температуре 90°С? Решение. Относительную устойчивость минералов можно определить по величине показателя неустойчивости (уравнение 10):
Чем большее значение имеет показатель неустойчивости, тем менее устойчиво данное соединение в растворе. Представим процесс растворения данных минералов в виде уравнений реакций:
Следует обратить внимание на то, что в обоих случаях в процессе растворения образуются одни и те же ионы. Поэтому для одной и той же воды, относительно которой будет рассматриваться устойчивость минералов, величина (ПА)прод в обоих случаях будет постоянной. Поскольку по условию задачи минералы не содержат примесей, (ПА)реаг в обоих случаях равны единице: (ПА)реаг = 1. Таким образом, показатель неустойчивости будет тем больше, чем больше константа равновесия реакции, и для ответа на вопрос задачи необходимо сравнить значения констант равновесия процессов растворения гипса и ангидрита. Поскольку константы равновесия процессов растворения зависят от температуры и давления, рассмотрим устойчивость минералов в различных условиях. а) Процесс растворения протекает при стандартных условиях. В этом случае константы равновесия могут быть определены из уравнения (4):
Для процесса растворения гипса значение константы равновесия при стандартных условиях составляет (см. Пример 2.8):
Для процесса растворения ангидрита имеем:
Подставив значения энергии Гиббса образования ионов и соединений в стандартных условиях (таблица 5 Приложения) в данное уравнение, получим:
= 27,21 (кДж/моль) = 27,21 . 103 (Дж/моль). Логарифм константы равновесия процесса растворения ангидрита равен:
Константа равновесия процесса растворения ангидрита равна:
Поскольку константа равновесия процесса растворения гипса меньше, чем ангидрита, гипс более устойчив в водном растворе при стандартных условиях. б) Процесс растворения протекает при нормальном давлении и температуре 90°С. Для определения констант равновесия процессов растворения гипса и ангидрита воспользуемся уравнением (5), связывающим константы равновесия, определенные при различных температурах процесса:
Значения энтальпии реакции можно определить по уравнению:
Для процесса растворения гипса имеем:
Подставив значения энтальпии образования ионов и соединений в стандартных условиях (таблица 6 Приложения) в данное уравнение, получим:
= 4,1 (кДж/моль) = 4,1 . 103 (Дж/моль). Логарифм отношения констант равновесия процессов растворения гипса при температуре 363 К (90°С) и температуре при стандартных условиях (298 К) составит:
Отношение констант равновесия процессов растворения гипса при температурах 363 К и 298 К будет: K1/K0 = 1,35. Константа равновесия процесса растворения гипса при температуре 363,3 К составит: К1 = 1,35K0 = 1,35 . 3,6 . 10–4 = 4,86 . 10–4. Проведем аналогичные расчеты для процесса растворения ангидрита:
Подставив значения энтальпии образования ионов и соединений в стандартных условиях (таблица 6 Приложения) в данное уравнение, получим:
=–15,7– 103 (Дж/моль);
K1/K0 = 0,32; К1 = 0,32K0 = 0,32 . 1,68 . 10–5 = 5,37 . 10–6. Таким образом, при 90°С константа равновесия процесса растворения ангидрита меньше, чем константа равновесия гипса при этой температуре: 5,37 . 10-6 < 4,86 . 10–4, поэтому в этих условиях ангидрит более устойчив, чем гипс. Ответ: при стандартных условиях гипс более устойчив, чем ангидрит, а при температуре 90°С и нормальном атмосферном давлении ангидрит становится более устойчивым.
Пример 10.Сколько миллиграммов ионов фтора может содержаться при нормальных условиях в природной воде, не содержащей примесей и находящейся в равновесии с флюоритом (CaF2), если: а) в исходной воде отсутствовали растворенные примеси; б) в исходной воде содержались ионы натрия и хлора в концентрации 0,05 М? Сравните полученные значения с предельно допустимой концентрацией ионов фтора в водоемах рыбохозяйственного назначения (ПДКр.х = 0,75 мг/л). Решение.Процесс растворения фторида кальция (флюорита) в воде можно представить следующим уравнением реакции:
Произведение растворимости для данного процесса можно представить уравнением: ПР(CaF2) = [Ca2+][F–]2 Поскольку, как следует из уравнения реакции, при растворении одного моля фторида кальция образуется один моль катионов кальция и два моля ионов фтора, а другие источники данных ионов отсутствуют, можно записать: [Ca2+]=[F–]/2 В этом случае произведениерастворимости для данного процесса можно представить в виде: ПP(CaF2) = [F–]3/2 Отсюда легко получить выражение для определения концентрации ионов фтора в равновесном растворе: [F–] (моль/л) = [2ПP(CaF2)]1/3 Произведение растворимости может быть рассчитано из определяемой по термодинамическим данным константы равновесия ( уравнение 15): ПР(CaF2)=K0/( Поэтому выражение для определения растворимости фтора можно представить в виде: [F–] (моль/л) = [2K0( Таким образом, для ответа на вопрос задачи необходимо: – определить константу равновесия процесса растворения в стандартных условиях, значение которой не зависит от содержания других ионов в растворе; – рассчитать значения коэффициентов активности ионов кальция и фтора, которые зависят от ионной силы раствора и могут различаться для случаев «а» и «б», определяемых условиями задачи. Значения константы равновесия реакции растворения флюорита определим из термодинамических данных (Пример 8): lg Значение lg
Подставив значения энергии Гиббса образования ионов и соединений в стандартных условиях (таблица 5 Приложения) в данное уравнение, получим:
= 55,8 . 103 (Дж/моль). Логарифм константы равновесия равен: lg Константа равновесия процесса растворения флюорита равна:
Для расчета коэффициентов активности ионов в растворе воспользуемся уравнениями Дебая – Хюккеля (16) и (17):
Определим значения коэффициентов активности ионов кальция и фтора для случая «а», когда в растворе присутствуют только ионы фтора и кальция, образовавшиеся при растворении флюорита. Поскольку неизвестна ионная сила раствора I, проведем определение коэффициентов активности, используя метод последовательных приближений. На первом шаге итерации примем значения коэффициентов активности ионов кальция и фтора равными единице: gСa2+ = 1 и gF– = 1. В этом случае концентрация ионов фтора в растворе составит: [F –] (моль/л) = (2K0)1/3; [F –] = (2 . 1,62 . 10–10)1/3 = 0,69 . 10–3 (моль/л). Концентрация ионов кальция будет равна: [Са2+] = [F –]/2 = 0,69 . 10–3/2 = 0,34 . 10–3 (моль/л). При таких концентрациях ионов кальция и фтора и отсутствии других ионов ионная сила раствора составит (уравнение 18):
При такой ионной силе раствора коэффициенты активности ионов кальция и фтора составят: lggCa2+= –A . 22 . I1/2; lggF– = –AI1/2. При стандартных условиях значение коэффициента А уравнения Дебая – Хюккеля равно 0,5058 (таблица 8 Приложения), и коэффициенты активности будут: lggCa2+ = –0,5058 . 4 . (2,05 . 10–3)1/2 = –0,091; gCa2+= 0,81. lggF– = –0,5058 . (2,05 . 10–3)1/2 = –2,23 . 10–2; gF–= 0,95. При таких значениях коэффициентов активности ионов фтора и кальция концентрации ионов фтора и кальция в растворе составят:
[F –] = [2K0/(gCa2+gF–)]1/3 = [2 . 1,62 . 10–10/(0,81 . 0,952)]1/3= 0,77 . 10–3 (моль/л); [Са2+] = [F –]/2 = 0,38 . 10–3 (моль/л). Полученные значения концентраций соответствующих ионов существенно отличаются от значений, полученных на предыдущем шаге, поэтому продолжим расчет. Ионная сила раствора при концентрации ионов фтора и кальция, равной, соответственно 0,77 . 10–3 и 0,38 . 10–3 моль/л, и отсутствии других ионов в растворе составит: I = 0,38 . 10–3 . 4 +0,77 . 10–3 = 2,29 . 10–3. Определим коэффициенты активности ионов фтора и кальция при такой ионной силе раствора: lg gCa2+= –0,5058 . 4 . (2,29 . 10–3)1/2 = –0,096; gCa2+= 0,80. lg gF– = –0,5058 . (2,29 . 10–3)1/2 = 1,16 . 10–3; gF– = 0,99. При этих значениях коэффициентов активности ионов фтора и кальция их концентрации в растворе фторида кальция составят:
[Ca2+] = 0,36 . 10–3моль/л. Полученные значения концентраций ионов отличаются от значений, полученных на предыдущем шаге расчетов (когда коэффициенты активности ионов были приняты равными единице), менее чем на 10%. В нашем случае такую разницу можно считать удовлетворительной и не проводить дальнейших шагов, приближающих к истинным значениям равновесных концентраций ионов фтора и кальция в растворе. Таким образом, можно принять, что концентрация ионов фтора при стандартных условиях и отсутствии других ионов, при равновесии с флюоритом составит: [F–] = 0,73 . 10–3 моль/л. Поскольку молярная масса фтора равна 19 г/моль, концентрация ионов фтора в растворе составит: CF– (мг/л) = [F–] (моль/л) . М(г/моль) . 103 = 0,73 . 10–3 . 19 . 103 = 14 мг/л Это значение более чем в 18 раз превышает значение ПДКр.х для ионов фтора: n = 14/0,75 = 19. Рассмотрим случаи «б», когда в исходной воде присутствует хлорид натрия. В этом случае помимо ионов кальция и фтора, образующихся при растворении флюорита, в растворе присутствуют ионы натрия и хлора, образующиеся при растворении хлорида натрия: NaCl = Na+ + Сl– Для расчета коэффициентов активности ионов кальция и фтора методом итераций примем на первом шаге концентрации ионов фтора и кальция равными значениям, рассчитанным для случая «а», когда другие ионы в растворе отсутствовали: [F–] = 0,73 . 10-3 моль/л и [Са2+] = 0,36 × 10–3 моль/л. Поскольку хлорид натрия относится к сильным электролитам, он практически полностью диссоциирует в водном растворе. Поэтому концентрации ионов хлора и натрия в растворе, по условию задачи, составят: [Na+]= [Сl–] = 0,05 моль/л Ионная сила в таком растворе будет равна:
Поскольку 0,01<5,32 . 10–2 < 0,1, для определения коэффициентов активности ионов фтора и кальция воспользуемся уравнением:
Значения коэффициентов уравнения Дебая-Хюккеля, определяемые условиями проведения процесса и природой ионов (таблица 8 Приложения), составляют: А = 0,5058; В= 0,3281 . 108; аСа2+= 6,0 × 10–8; aF– = 3,5 . 10–8. Значения коэффициентов активности ионов кальция и фтора в этом случае составят: lggСа2+= –0,5058 . 4 . (5,1 . 10–2)1/2 . . [1 +0,3281 . 108 . 6,0 . 10–8 . (5,1 . 10–2)1/2] = –0,32; gСа2+= 0,48; lg gF–= gF– = 0,81. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 aA + bB cC + dD (2)
aA + bB cC + dD (2) (3)
(3) (4)
(4)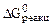 – энергия Гиббса реакции, взятая с обратным знаком, Дж/моль;
– энергия Гиббса реакции, взятая с обратным знаком, Дж/моль; , (5)
, (5) lg(K338/K0)
lg(K338/K0)  , (6)
, (6)
 , (8)
, (8) . (10)
. (10) . (12)
. (12) = (ПА)прод/Kравн, (13)
= (ПА)прод/Kравн, (13) g
g  ), (15)
), (15) , если I < 0,01 (16)
, если I < 0,01 (16) если 0,01 < I < 0,1 (17)
если 0,01 < I < 0,1 (17) , (18)
, (18) , (19)
, (19) ,
, – равновесные значения концентрации кислорода в воде;
– равновесные значения концентрации кислорода в воде; – значения константы Генри процесса растворения кислорода в воде при 5 и 250С соответственно.
– значения константы Генри процесса растворения кислорода в воде при 5 и 250С соответственно. =0,00191 моль/(л×атм) при 50С,
=0,00191 моль/(л×атм) при 50С, =0,00130 моль/л×атм) при 250С.
=0,00130 моль/л×атм) при 250С. (поскольку по условию задачи парциальным давлением паров воды в воздухе можно пренебречь, объемную долю кислорода можно принять равной объемной доле кислорода для сухого воздуха в приземном слое атмосферы):
(поскольку по условию задачи парциальным давлением паров воды в воздухе можно пренебречь, объемную долю кислорода можно принять равной объемной доле кислорода для сухого воздуха в приземном слое атмосферы): =1атм × 0,2095=0,2095 (атм).
=1атм × 0,2095=0,2095 (атм). = (0,00191 – 0,00130) × 0,2095 = 1,28 × 10–4 (моль/л).
= (0,00191 – 0,00130) × 0,2095 = 1,28 × 10–4 (моль/л). =1,28 × 10–4 × 32 × 103 = 4,1(мг/л).
=1,28 × 10–4 × 32 × 103 = 4,1(мг/л). составляет:
составляет: =10–3 моль/л;
=10–3 моль/л;  =10–2,8 моль/л;
=10–2,8 моль/л; =10–1,5 моль/л;
=10–1,5 моль/л; 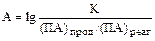
 CaSO4 . 2Н2О Са2+ + SO
CaSO4 . 2Н2О Са2+ + SO  .
. = 10–3 × 10–1,5 = 10–4,5 (моль/л)2;
= 10–3 × 10–1,5 = 10–4,5 (моль/л)2; = 10–2,8 × 10–2 = 10–4,8 (моль/л)2.
= 10–2,8 × 10–2 = 10–4,8 (моль/л)2. CaSO4 . 2Н2О Са2+ + SO
CaSO4 . 2Н2О Са2+ + SO  .
. определим из выражения:
определим из выражения:
 Подставив значения энергии Гиббса образования ионов и соединений в стандартных условиях (таблица 5 Приложения) в данное уравнение, получим:
Подставив значения энергии Гиббса образования ионов и соединений в стандартных условиях (таблица 5 Приложения) в данное уравнение, получим: = –28,65 . 103/(2,3 . 8,31 . 298,3) = –5,0.
= –28,65 . 103/(2,3 . 8,31 . 298,3) = –5,0. = 9,4 . 10–6.
= 9,4 . 10–6. .
. CaSO4 . 2Н2О Са2+ +
CaSO4 . 2Н2О Са2+ +  + 2H2O
+ 2H2O .
. .
. .
. .
.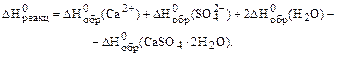
 = (–542,7) + (–909,3) + 2(–285,8) – (–2027,7) =
= (–542,7) + (–909,3) + 2(–285,8) – (–2027,7) =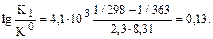
 .
. .
. CaF2 Ca2++2F–
CaF2 Ca2++2F– )
) определим из выражения:
определим из выражения: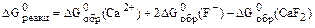 .
. =
= 
 (0,34 . 10–3 . 4 + 0,69 . 10–3) = = 2,05 . 10–3 < 0,01.
(0,34 . 10–3 . 4 + 0,69 . 10–3) = = 2,05 . 10–3 < 0,01. моль/л;
моль/л; =
=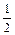 (0,36 × 10–3× 4 +0,73 × 10–3 +0,05 +0,05) = 5,1 . 10–2.
(0,36 × 10–3× 4 +0,73 × 10–3 +0,05 +0,05) = 5,1 . 10–2. .
. = –0,092;
= –0,092;