
|
|
Об иерархии групп объектов в исследуемой совокупностиПусть заданы множества признаков
а) каждая группа объектов, изображенная на графе вершиной, описывалась признаками из множества N; б) общая мера различия по признакам множества М между группами, находящимися на одном уровне, была наибольшей из всех возможных. Заметим, что количество ветвей, исходящих из вершин, расположенных на одном уровне, может быть различным и даже равным 1. Выполнить первое условие несложно. Для этого достаточно, используя N, произвести f – признаковую группировку объектов и получить множество Допустим, что множество М таково, что любое его подмножество дает информацию об N меньшую J(N,M). Тоже допущение примем для N. Если N и М таковы, то отпадает необходимость в поиске таких N' и М' , чтобы
J(N,M)= J(N',M') и количества признаков в N' и М' были минимальны. Объединим подмножества объектов множества α(1) в соответствии с изложенным ранее алгоритмом классификации. Пусть на шаге ν1 величина R(s) = (Xq,Xz) как функция номера шага S достигла максимума. Получим множества объектов В М найдем подмножество, состоящее из (m – 1) признака и дающее максимальную информацию о Объединение прекращается на шаге Пусть подмножества объектов В множестве М(1) найдем подмножество М(2), состоящее из m – 2 признаков и дающее максимальную информацию о Используя найденное М(2) произведем объединение групп объектов
Получим группы объектов третьего уровня снизу. Продолжая этот процесс, получим все m уровней графа, так как в исходном множестве М содержалось m признаков и на каждом цикле объединения удалялся всего один признак.
Неявные допущения Пусть произведено W объединений и получены Однако не существует доказательства, что во множестве М не найдется такого подмножества М* с количеством признаков, что и в M(w), и такое, что В М выделяются все подмножества, содержащие m – W признаков. По каждому из них производится объединение подмножеств объектов множества В R находится максимальный элемент. Пусть это будет Ræ. То подмножество признаков, при объединении которых был получен Ræ, и естъ искомое подмножество, наиболее выгодное для объединения подмножеств из
Сомнительно, что последний алгоритм можно воплотить на машине. Именно поэтому были предложены сравнительно простые правила получения иерархии групп объектов.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и
и  . Используя их, необходимо построить и описать древовидную структуру групп объектов ( см. рис.5), чтобы:
. Используя их, необходимо построить и описать древовидную структуру групп объектов ( см. рис.5), чтобы:
 . Если для организации графа (см. рис.5) использовать как исходные группы объектов
. Если для организации графа (см. рис.5) использовать как исходные группы объектов  , то первое условие будет выполнено.
, то первое условие будет выполнено. . Введем эквивалентный признак
. Введем эквивалентный признак  . Изобразим эти группы объектов вершинами нижнего ряда графа (см. рис. 5). Очевидно, они удовлетворяют второму условию.
. Изобразим эти группы объектов вершинами нижнего ряда графа (см. рис. 5). Очевидно, они удовлетворяют второму условию. . Считая множество подмножеств объектов
. Считая множество подмножеств объектов 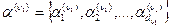 за исходное, проведем внутри его объединение. При этом мера близости между
за исходное, проведем внутри его объединение. При этом мера близости между  и
и  устанавливается по признакам подмножества М(1).
устанавливается по признакам подмножества М(1). , когда
, когда  достигает максимума. Получаем множество подмножеств объектов
достигает максимума. Получаем множество подмножеств объектов  , которое также удовлетворяет второму условию. Эти группы объектов изобразим вершинами предпоследнего уровня дерева графа.
, которое также удовлетворяет второму условию. Эти группы объектов изобразим вершинами предпоследнего уровня дерева графа. объединились в подмножество
объединились в подмножество  в результате второго объединения. Изобразим это на графе дугами, соединив вершины, соответствующие
в результате второго объединения. Изобразим это на графе дугами, соединив вершины, соответствующие  в последнем уровне графа, с вершиной
в последнем уровне графа, с вершиной  среди всех подмножеств признаков принадлежащих М(1).
среди всех подмножеств признаков принадлежащих М(1). в группы объектов
в группы объектов  .
. и эквивалентный признак
и эквивалентный признак  . Очевидно, что для объединения W использовалось множество М(w-1) из (m – W + 1) признака. Следуя изложенному алгоритму, нужно найти М(w) для которого
. Очевидно, что для объединения W использовалось множество М(w-1) из (m – W + 1) признака. Следуя изложенному алгоритму, нужно найти М(w) для которого  и
и  – максимально. Это первое неявное допущение при изложении алгоритма.
– максимально. Это первое неявное допущение при изложении алгоритма. . Кроме того, если даже допустить, что
. Кроме того, если даже допустить, что  максимально, т.е.
максимально, т.е.  , то нельзя гарантировать, что объединение по множеству признаков М(w) эффективнее объединения с использованием М*, т.е. возможно, что
, то нельзя гарантировать, что объединение по множеству признаков М(w) эффективнее объединения с использованием М*, т.е. возможно, что  все равно окажется больше
все равно окажется больше  . Это второе допущение. Можно предложить такой алгоритм объединения групп объектов:
. Это второе допущение. Можно предложить такой алгоритм объединения групп объектов:  .
. и запоминается максимум, которого достигает общая мера различия между группами объектов. Очевидно, таких величин нужно найти
и запоминается максимум, которого достигает общая мера различия между группами объектов. Очевидно, таких величин нужно найти  . Введем множество
. Введем множество  где
где  .
.